
- •Спецглавы математики
- •Лекция 1.............................................................................................................4
- •Аннотация
- •Лекция 1 План лекции
- •Функции комплексного переменного.
- •1.Область на комплексной плоскости.
- •Лекция 2 План лекции
- •2. Понятие и функции комплексного переменного.
- •3. Дифференцируемость и аналитичность.
- •Лекция 3 План лекции
- •Элементарные функции комплексного переменного.
- •3. Логарифмическая функция.
- •Пусть , а, тогда,
- •4.Тригонометрические функции.
- •5. Гиперболические функции.
- •6. Обратные тригонометрические функции.
- •Контурным интегралом функции комплексногопеременного называется, если существует, не зависит от способа деления контура с точкамии от выбора точекна дуге.
- •Лекция 7 План лекции
- •Представление аналитических функций рядами.
- •Лекция 9 План лекции
- •Лемма жордана.
- •Интеграл фурье. Преобразование фурье.
- •Лекция 9 План лекции
- •Лемма жордана.
- •Интеграл фурье. Преобразование фурье.
- •Лекция 10 План лекции
- •Некоторые специальные функции.
- •1. Единичная ступенчатая функция.
- •2. Дельта функция.
- •Лекция 11 План лекции
- •Обобщенное преобразование фурье. Преобразование лапласа.
- •Свойства преобразований лапласа.
- •Лекция 13
- •Лекция 14
- •Применение преобразования лапласа для решения линейных дифференциальных уравнений с постоянными коэффициентами.
- •Обратное преобразование лапласа рациональной алгебраической дроби.
- •Изображение импульса произвольной формы.
- •Разностные уравнения.
- •Линейные разностные уравнения с постоянными коэффициентами.
- •Лекция 16
- •Дискретное преобразование лапласа. Z – преобразование.
- •Лекция 17
- •Связь между обычным преобразованием лапласа и d и z- преобразованиями. Преобразование.
- •Свойства z – преобразования.
Лекция 16
План лекции
Понятие о D и Z - преобразованиях.
Область применения D и Z - преобразований.
Обратные D и Z - преобразования.
Дискретное преобразование лапласа. Z – преобразование.
В прикладных исследованиях, связанных с использованием решетчатых функций, широко применяется дискретное преобразование Лапласа (Д – преобразование) и Z – преобразование. По аналогии с обычным преобразованием Лапласа дискретное задается в виде
![]() где
(1)
где
(1)
![]()
Символически Д – преобразование записывается в виде
![]()
Для смещенных решетчатых функций
![]() (2)
(2)
где
![]() -
смещение.
-
смещение.
Z
– преобразование получается из Д –
преобразования подстановкой
![]() и
задается соотношением
и
задается соотношением
![]() (3)
(3)
Для смещенной функции
![]()
Функция
![]() называется оригиналом, если
называется оригиналом, если
1)
![]()
2)
существует показатель роста, т. е.
найдутся такие
![]() и
и![]() ,
что
,
что
![]() (4)
(4)
Наименьшее
из чисел
![]() (или предел, к которому стремится
наименьшее число), для которого
справедливо неравенство (4), называется
абсциссой абсолютной сходимости и
обозначается
(или предел, к которому стремится
наименьшее число), для которого
справедливо неравенство (4), называется
абсциссой абсолютной сходимости и
обозначается![]()
Теорема.
Если
функция
![]() является оригиналом, то изображение
является оригиналом, то изображение![]() определено в областиRe
p
>
определено в областиRe
p
>
![]() и является в этой области аналитической
функцией.
и является в этой области аналитической
функцией.
Покажем,
что при Re
p
>
![]() ряд (1) абсолютно сходится. Имеем
ряд (1) абсолютно сходится. Имеем
![]()
![]()
![]()
т.
к. указанная сумма представляет собой
сумму членов убывающей геометрической
прогрессии с показателем
![]() Известно,
что такая прогрессия сходится. Величину
Известно,
что такая прогрессия сходится. Величину![]() можно взять сколь угодно близкой
величине
можно взять сколь угодно близкой
величине![]() ,
т. е. первая часть теоремы доказана.
,
т. е. первая часть теоремы доказана.
Вторую часть теоремы примем без доказательств.
Изображение
![]() является периодической функцией с
мнимым периодом
является периодической функцией с
мнимым периодом![]()
![]()
![]()
При
изучении изображения
![]() нет смысла рассматривать его на всей
комплексной плоскости, достаточно
ограничиться изучением в любой полосе
шириной
нет смысла рассматривать его на всей
комплексной плоскости, достаточно
ограничиться изучением в любой полосе
шириной![]() Обычно на комплексной плоскости
используется полоса,
Обычно на комплексной плоскости
используется полоса,![]() которая называется основной. Т. о. Можно
считать, что изображения
которая называется основной. Т. о. Можно
считать, что изображения![]() определено в полу полосе
определено в полу полосе
![]() и
является в этой полу полосе аналитической
функцией.
и
является в этой полу полосе аналитической
функцией.
Re p
Im p
π/T
-π/T
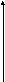
























Re p
Im p
σa





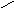
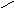
Найдем
область определения и аналитичности
функции F(z),
положив
![]() .
Покажем, что полу полоса
.
Покажем, что полу полоса![]() плоскостиp
преобразованием
плоскостиp
преобразованием
![]() переводится
в область на плоскостиz:
переводится
в область на плоскостиz:
![]() .
.
Действительно,
отрезок
![]() ,
ограничивающий полу полосу на плоскостиp,
переводится на плоскости z
в окрестность:
,
ограничивающий полу полосу на плоскостиp,
переводится на плоскости z
в окрестность:
![]() .
.
Обозначим
через
![]() линию, в которую преобразование
линию, в которую преобразование![]() переводит
отрезок
переводит
отрезок![]() .
Тогда
.
Тогда
![]()
![]()
![]()
![]() т.
о.
т.
о.
![]() окрестность
окрестность
![]() .
.
Т.
о. Z
– преобразование F(z)
определено в области
![]() и является в этой области аналитической
функцией.
и является в этой области аналитической
функцией.
Обратное
Д – преобразование позволяет по
изображению
![]() восстановить решетчатую функцию
восстановить решетчатую функцию![]()
Im p
π/T
-π/T
σa



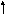
Re p
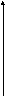



Докажем справедливость равенства.
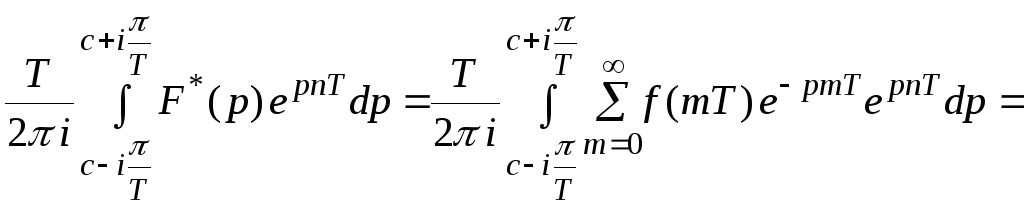

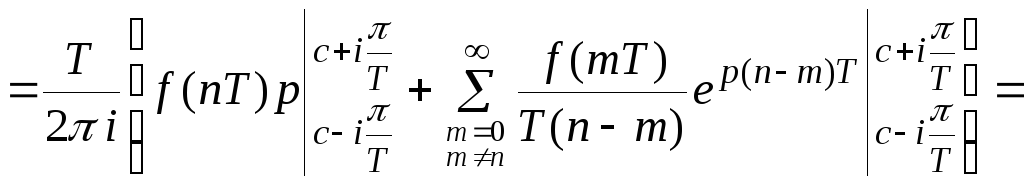
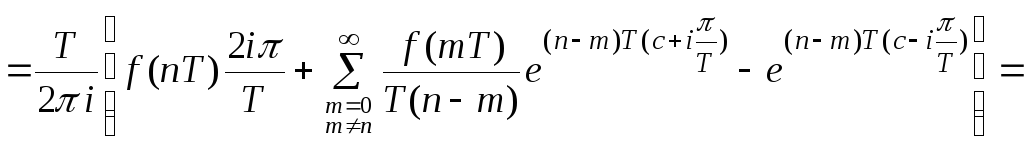
![]()
![]()
Получим
из равенства (5) формулу для обратного
Z
– преобразования. Воспользуемся
подстановкой
![]() .
Рассмотренным выше способом легко
установить, что отрезок
.
Рассмотренным выше способом легко
установить, что отрезок![]() с
помощью преобразования
с
помощью преобразования![]() переводится
на плоскостиZ
в окрестность
переводится
на плоскостиZ
в окрестность
![]()
![]() .
.
Тогда из (5) следует
![]() (6)
(6)
Равенство (6) задает обратное Z – преобразование, т. е. позволяет по функции F(z) восстановить решетчатую функцию f(nT).
Т.
к.
![]() ,
то все особые точки функцииF(z)
и, следовательно, функции
,
то все особые точки функцииF(z)
и, следовательно, функции
![]() лежат
внутри окрестности
лежат
внутри окрестности![]()
Из (6) следует, что
![]()
Вычеты берутся по всем особым точкам.
