Лекция 14

План лекции

1. Теорема о начальном и предельном значениях.

2. Применение преобразования Лапласа для решения дифференциальных уравнений.

3. Обратное преобразование Лапласа рациональной алгебраической дроби.

4. Изображение импульса произвольной формы. Изображение периодических функций.

10.Предельное значение оригинала.

Теорема 10.

Если функции f(t) и f′ (t) являются оригиналами, и функция f(t) имеет изображения F(s), и если произведение s F(s) является аналитической функцией в правой полуплоскости на мнимой оси, то

.

Доказательство.

По теореме изображения производной

Перейдем пределу при , данный предел существует, т. к. функцияsF(s) – аналитическая в окрестности 0. Получим

Переход к пределу под знаком интеграла возможен, т. к. по условию теоремы абсцисса абсолютной сходимости для функции , поэтому

- существует.

наименьшее α- абсцисса абсолютной сходимости.

Re s > , α < 0.

Из равенства

следует, что

.

Для функции

- не существует.

Теорема не справедлива, т. к. функция имеет два полюса на мнимой оси.

Пример.

Найти , если

=

11.Начальное значение оригинала.

Теорема 11.

Если функции f(t) и f′ (t) являются оригиналами, и функция f(t) имеет изображения F(s), то

при условии, что т. о., чтоRe s = c.

Доказательство.

По определению

Перейдем к пределу

Покажем, что

Справедливо равенство

Из равенства

следует, что

Применение преобразования лапласа для решения линейных дифференциальных уравнений с постоянными коэффициентами.

Рассмотрим пример. Требуется решить уравнение

Обозначим .

В соответствии с теоремой 2

Пусть заданы начальные условия

Применим к правой и левой частям уравнения преобразование Лапласа

Обратное преобразование лапласа рациональной алгебраической дроби.

Изображение решения линейного дифференциального уравнения имеет вид

,

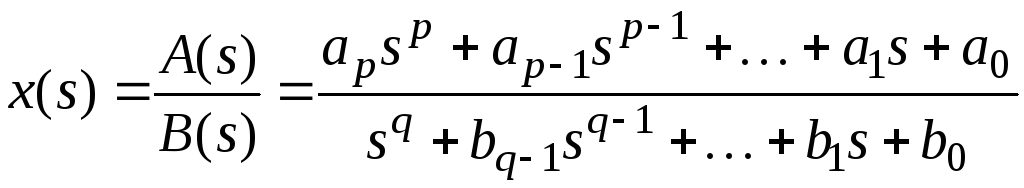где - некоторые числа.

Если то дробь неправильная. Поделим числитель на знаменатель

Принимая во внимание изображение и ее производной, получим

- правильная дробь.

Т. о. задача заключается в нахождении обратного преобразования Лапласа от правильной дроби.

В соответствии с формулой обратного преобразования Лапласа

Для вычисления интеграла воспользуемся леммой Жордана. Рассмотрим замкнутый контур L, изображенный на рисунке.

L =

Вычеты берутся по всем точкам, лежащим левее прямой Re S = C.

Тогда

В соответствии с основной теоремой (1) изображение является аналитической функцией в области Re S > , т. к. C > , то все особые точки функции лежат левее прямой Re S = C, т. е. вычеты необходимо брать по всем особым точкам.

Рассмотрим два частных случая.

1. B(s) = 0, имеет простые вещественные корни.

Обозначим корни уравненияB(s) = 0. Применяя формулу вычетов, найдем

2. Два корня являются мнимыми.

Пусть уравнение B(s) = 0, имеет корни

корни вещественные и простые.

Изображение такого вида имеет место, когда в правой части дифференциального уравнения стоит гармоническая функция: sin или cos.

Применяя формулу 3 вычетов, найдем

Два первых слагаемых комплексно сопряжены, поэтому при их суммировании мнимые части сокращаются, а вещественные удваиваются.

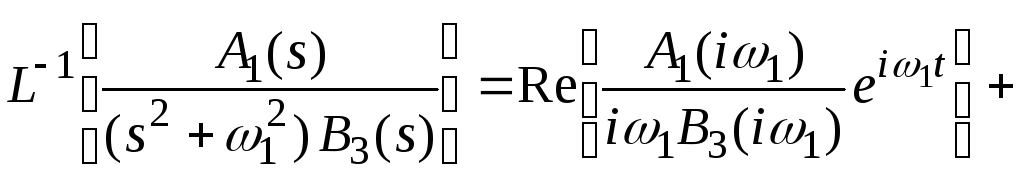
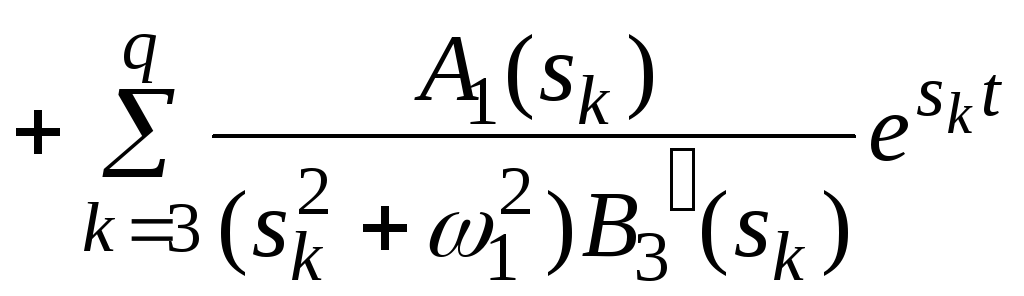
Иногда вместо операции взятия вещественной части удобно взять мнимую часть. Принимая во внимание, что

,запишем

Замечание.

Полученные формулы можно использовать и в случае комплексных корней уравнения, однако в этом случае возникает необходимость выделять вещественную часть, что часто приводит к громоздким вычислениям. В этом случае целесообразно использовать разложение дроби на сумму простых дробей.