4. Скалярное произведение векторов.

Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является скаляр (число), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Скалярным произведением векторов и называется произведение их длин на косинус угла между ними:

Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины.

Скалярное произведение двух векторов и его свойства.

Скалярным произведением двух нулевых векторов называется число, равное

произведению числовых значений длин этих векторов на косинус угла между

векторами.

Обозначение: а х в = IaI * IbI * cos ( а, в).

Свойства скалярного произведения:

1. а х в = в х а.

2. Для того, чтобы два нулевых вектора а и в были перпендикулярны,

необходимо и достаточно, чтобы скалярное произведение этих векторов было

равно нулю, т.е. а х в = 0.

3. Выражение а х а будем обозначать а2 и называть скалярным квадратом

вектора а.

15 . Длина вектора. Угол между векторами. Угол между вектором и осью.

Длина вектора в координатах определяется как расстояние между точками начала и конца вектора. Если заданы две точки в пространстве А(х₁, y₁, z₁), B(x₂, y₂, z₂), то

Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.

При параллельном переносе любого из двух векторов угол между ними остается неизменным, только в этом случае поворот одного из векторов осуществляется либо в общей для обоих векторов плоскости, либо в плоскости параллельной другому вектору.

Введем понятие угла между вектором и осью.

Определение. Углом между вектором и осью называется угол между данным вектором и любым правоориентированным вектором этой оси.

1. Расстояние между двумя точками. Коллинеарные вектора.

Расстояние d между двумя точками (, , ) и (, , ) в пространстве определяется формулой

.Координаты x, y, z точки М, которая делит отрезок , ограниченный точками (, , ) и (, , ), в отношении , определяется по формулам

, , .

В частности, при имеет координаты середины данного отрезка:

, , .

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы либо одинаково направлены, либо противоположно направлены

Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).

17. Деление отрезка в данном отношении.

Если точка М(x; y) лежит на прямой, проходящей через две данные точки (, ) и (, ), и дано отношение , в котором точка М делит отрезок , то координаты точки М определяются по формулам,

Если точка М является серединой отрезка , то ее координаты определяются по формулам

, .

Даны точки А₁(x₁;y₁), А₂(x₂;y₂). Требуется найти координаты х, у точки К, делящей отрезок А₁А₂ в отношении l=m₁:m₂.

Решение дается формулами:

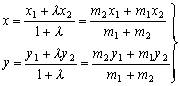
Выражение "точка К делит отрезок А₁А₂ в отношении m₁:m₂" означает, что отношение m₁:m₂ равно отношению отрезков А₁К:КА₂, взятых именно в этом (а не в обратном) порядке.

Пусть точка К делит отрезок А₁А₂ внешним образом, т.е. лежит на продолжении отрезка А₁А₂;тогда указанные формулы сохраняют силу, если величине m₁:m₂=l приписать отрицательный знак.