7.Градиент и линии уровня цф

Градиент - вектор, который определяет направление наискорейшего роста функции, его координаты находятся как частные производные функции.  Z(x) = C1*x1 + C2*x2, C = grad Z = (ðZ/ðx1; ðZ/ðx2) = (c1,c2)

Линия уровня ЦФ наз-ся линией, имеющей уравнение: Z(x)= const; с1*x1 + c2*x2 = const

ЛУ _|_ C (линия уровня перпендикулярна градиенту).

8.Определение точки оптимума на графике. Особые случаи.

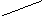
ЛУ перемещаем ||-но самой себе в направлении вектора, если Z(x) →max; если Z(x)→min, то в противоположном напр-нии до точки выхода из ОДР, это и будет точка оптимума (*)

a₁*x₁ + a₂*x₂ = b B=x₁, C=x₂

- случай альтернативного оптимума

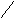x*=α*x*₁+(1-α)* x*₂; α € [0; 1] ЛУ: с1*x1 + c2*x2= const

Проверить а1/а2 = с1/с2

9.Алгоритм графического метода решения злп с 2 переменными

1. Построить область допустимых решений

2. Если область допустимых решений является пустым множеством, то задача не имеет решения ввиду несовместности системы ограничений

3. Если ОДР яв-ся непустым множеством, построить нормаль линии уровня n = (c₁,c₂) и одну из линий уровня, имеющую общие точки с этой областью

4. ЛУ переместить до опорной прямой в задаче на max в направлении нормали, в задаче на min – в противоположном направлении

5. Если при перемещении ЛУ по ОДР в направлении, соответствующем приближению к extr ЦФ, ЛУ уходит в бесконечность, то задача не имеет решения ввиду неограниченности ЦФ

6. Если ЗЛП имеет оптимальное решение то для его нахождения решить совместно уравнения прямых, ограничивающих область ОДР и имеющих общие точки с опорной прямой. Если ЦФ достигает экстремума в 2х точках, то задача имеет бесконечное множество решений. После нахождения оптимальных решений вычислить значения ЦФ на этих решениях

10.Выпуклые множества в n-мерном пространстве

Общим определяющим свойством, которое отличает выпуклый многоугольник от невыпуклого, является то, что если взять любые две его точки и соединить их отрезком, то весь отрезок будет принадлежать этому многоугольнику. Это свойство может быть принято за определение выпуклого множества точек.

Множество точек называется выпуклым, если оно вместе с лю­быми двумя своими точками содержит весь отрезок, соединяющий эти точки. Выпуклые множества обладают важным свойством: пересечение (общая часть) любого числа выпуклых множеств есть выпуклое множество.

Точка множества называется внутренней, если в некоторой ее окрестности содержатся точки только данного множества.

Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему.

Особый интерес в задачах линейного программирования представляют угловые точки. Точка множества называется угловой (или крайней), если она не является внутренней ни для какого отрезка(отрезок-выпуклая лин комбинация), целиком принадлежащего данному множеству.

Для выпуклого множества угловые точки всегда совпадают с вершинами многоугольника (многогранника), в то же время для невыпуклого множества это не обязательно. Множество точек называется замкнутым, если включает все свои граничные точки. Множество точек называется ограниченным, если существует шар (круг) радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество; в противном случае множество называется неограниченным.

Выпуклое замкнутое множество точек плоскости, имеющее конечное число угловых точек, называется выпуклым многоугольником, если оно ограниченное, и выпуклой многоугольной областью, если оно неограниченное.

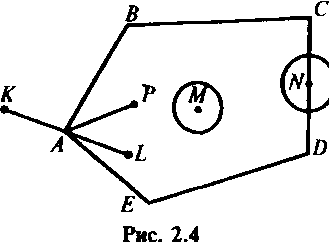
внутренняя (точки М), граничная (точка N) и угловые (точки А, В, С, D, Е). Точка А - угловая, так как для любого отрезка, целиком принадлежащего многоугольнику, например, отрезка АР, она не является внутренней; точка А - внутренняя для отрезка KL, но этот отрезок не принадлежит целиком многоугольнику.