
- •Учебно-методический комплекс дисциплины сд.12 дискретная математика
- •061800 «Математические методы в экономике»
- •Раздел 1. Программа учебной дисциплины. Структура программы учебной дисциплины
- •1.3 Пояснительная записка:
- •1.5. Объем дисциплины и виды учебной работы.
- •1.6 Содержание дисциплины.
- •1.7 Методические рекомендации по организации изучения дисциплины.
- •1.8 Учебно-методическое обеспечение дисциплины.
- •1.9 Материально-техническое обеспечение дисциплины.
- •1.10 Примерные зачетные тестовые задания.
- •1.11 Примерный перечень вопросов к зачету (экзамену).
- •1.12 Комплект экзаменационных билетов
- •1.13 Примерная тематика рефератов.
- •1.14 Примерная тематика курсовых работ.
- •Элементы теории множеств
- •§ 2. Бинарные операции и их свойства
- •§ 3. Операции над множествами. Законы де Моргана
- •§ 4. Вектор. Прямое произведение
- •§ 5. Мощность конечного множества
- •§ 6. Отношения и их свойства
- •§ 7. Отношение эквивалентности
- •§ 8. Отношение порядка
- •§ 9. Отображения и их свойства
- •Глава II. Элементы теории графов
- •§ 1. Графы, их вершины, рёбра и дуги
- •§ 2. Операции над графами
- •§ 3. Способы задания псевдографов. Степени вершин
- •§ 4. Отношение связности для вершин неориентированного графа
- •§ 5. Отношение достижимости для вершин орграфа
- •§ 6. Эйлеров граф и условия его существования
- •§ 7. Гамильтонов граф и условия его существования
- •§ 8. Деревья и их свойства. Цикломатическое число
- •§ 9. Формула Кэли
- •§ 10. Двудольный граф
- •§ 11. Планарность
- •§ 12. Раскраска графов
- •Глава III. Булевы функции
- •§ 1. Основные определения
- •§ 2. Свойства булевых функций
- •§ 3. Переключательные функции
- •§ 4. Совершенные нормальные формы
- •§ 5. Полнота. Примеры полных систем
- •§ 6. Замыкание и его свойства
- •§ 7. Важнейшие замкнутые классы
- •§ 8. Теорема о функциональной полноте
- •Раздел 4. Словарь терминов (глоссарий) Элементы теории множеств
- •Конечные графы
- •Функциональные системы с операциями: алгебра логики
- •Раздел 5. Практикум по решению задач (практических ситуаций) по темам лекций (одна из составляющих частей итоговой государственной аттестации) Элементы теории множеств
- •Задачи для самостоятельного решения
- •Конечные графы
- •Задачи для самостоятельного решения
- •Функциональные системы с операциями: алгебра логики
- •Задачи для самостоятельного решения
- •Раздел 6. Изменения в рабочей программе, которые произошли после утверждения программы.
- •Раздел 7. Учебные занятия по дисциплине ведут:
§ 4. Вектор. Прямое произведение
Вектор - это упорядоченный набор элементов. Сказанное не следует считать определением вектора, поскольку тогда потребуется давать объяснения по поводу его синонима “упорядоченный набор”. Понятие “вектор”, как и понятие “множество”, является одним из неопределяемых понятий математики. Элементы, образующие вектор, называются координатами или компонентами вектора.
В отличие от элементов множества координаты вектора могут совпадать. Векторы длины 2 часто называют упорядоченными парами (или просто парами), векторы длины 3 - тройками и т.д. Два вектора равны, если они имеют одинаковую длину и их соответствующие координаты равны, т.е. (a1,a2,...,an,...) и (b1,b2,...,bm,...) равны, если m=n и a1= b1, a2= b2, ..., an = bn .
Прямым произведением множеств А и В (обозначение: АВ) называется множество всех пар (a,b), таких, что аА, bB. В частности, если А=В, то обе координаты принадлежат А. Такое произведение обозначается A2. Аналогично прямым произведением множеств A1,A2,...,An (обозначение: A1A2...An) называется множество всех векторов (a1,a2,...,an,...) длины n, таких, что a1A1, a2A2,..., anAn. При A1=A2=...=An вместо A1A2...An записывают An.
Примеры.
1. Пусть R - множество действительных чисел. Тогда R2=RR - это множество точек плоскости, точнее, пар вида (a,b), где a, b принадлежат R и являются координатами точек плоскости.
Координатное представление точек плоскости, предложенное французским математиком и философом Декартом, исторически первый пример прямого произведения. Поэтому иногда прямое произведение называют декартовым.
2. Пусть A ={a,b,c,d,e,f,g,h}, B={1, 2, 3, 4, 5, 6, 7, 8}. Тогда АВ={a1,a2,a3,... ,h7,h8) - множество, содержащее обозначение всех 64 клеток шахматной доски.
3. Пусть А - конечное множество, элементами которого являются символы (буквы, цифры, знаки препинания и т.д.). Такие множества называются алфавитами. Элементы множества An называются словами длины n в алфавите А.
Множество всех
слов в алфавите А
- это множество
![]() =A1
A2
A3...
=A1
A2
A3...
При написании слов не принято пользоваться ни запятыми, ни скобками, ни разделителями, однако они могут оказаться символами самого алфавита. Поэтому слово в алфавите А - это просто конечная последовательность символов алфавита А. Напимер, десятичное натуральное число - это слово в алфавите цифр {0,1,2,...,9}. Текст, напечатанный на пишущей машинке, является словом в алфавите, определяемом клавиатурой данной машинки (включая знаки препинания и пробел).
Прямое произведение не обладает свойством коммутативности (АВ ВА), но для него выполняются свойства дистрибутивности относительно объединения и пересечения:
(АВ) С = (АС) (ВС), А(ВС) = (АВ) (АС);
(АВ) С = (АС) (ВС), А(ВС) = (АВ) (АС).
(Доказать самостоятельно. У к а з а н и е. Воспользоваться схемой доказательства дистрибутивности операций ““ и ““; см. § 3).
§ 5. Мощность конечного множества
Мощностью конечного множества A={a1,a2,...,an,...}, называется число его элементов n (обозначение: |A|=n). Очевидно, что если А=В, то |A|=|B|. Кроме того, || = 0.
Примеры.
1. A ={-2,-1,0,1,2}, |A| = 5;
2. B ={b / b делится на 3 без остатка и b 21, bN}, |B| = 7.
Теорема 1.1 (о мощности разности). Пусть А и В - конечные множества и, кроме того, В А. Тогда |A\B| = |A| - |B|.
Теорема 1.2 (о мощности объединения непересекающихся множеств). Пусть А и В - конечные множества и, кроме того, АВ=. Тогда |AB| = |A|+| В|.
Теорема 1.3 (о мощности объединения пересекающихся множеств). Пусть А и В - конечные множества. Тогда
|AB| = |A|+|B| - |АВ|. (1.1)
Представим объединение двух, в общем случае пересекающихся, множеств А и В в виде объединения непересекающихся множеств А и B\(АВ): AB = (A) (B\(АВ)).
Тогда по теореме 1.2 |AB| = |(A) (B\(АВ))| = |A| +|B\(АВ)|.
Так как (АВ)В, то по теореме 2.1 |B\(АВ)| = |B|-|АВ|.
Окончательно имеем |AB| = |A| +|B\(АВ)| = |A|+|B|-| АВ|.
Пример. В игральной колоде 36 карт. Сколькими способами можно извлечь из колоды туза или карту бубновой масти?
Решение. Пусть А - множество тузов в колоде, а В - множество карт бубновой масти. Очевидно, что
А = {T, T, T, T}, B = {6, 7, 8, 9, 10, B, D, K, T},
АВ = {T}; |A| = 4, |B| = 9, |АВ| = 1.
По формуле (1.1) |AB| = |A| + |B| - |АВ| = 4 + 9 - 1 = 12.
Обобщим теорему 1.3 на случай n множеств. Предположим, что даны подмножества A1,A2,...,An (необязательно различные) некоторого конечного множества X. Тогда имеет место следующая теорема.
Теорема
1.4 (принцип
включения и исключения).![]()
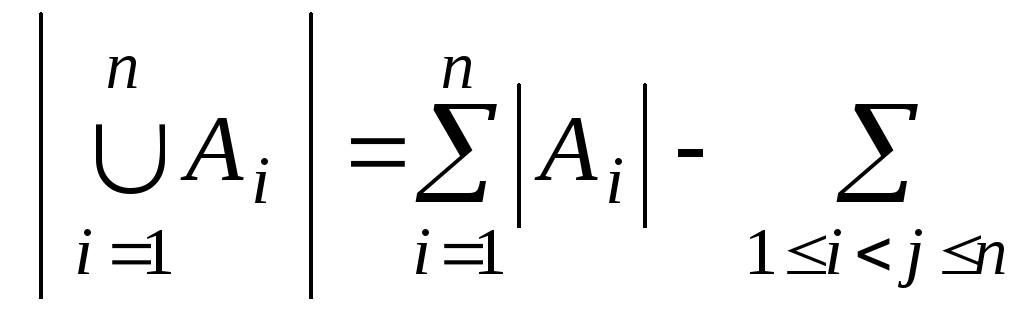 |
Ai
Aj |
+
|
Ai
Aj |
+
![]() |
Ai
Aj
Ak
|-...+(-1)n-1
|A1
A2...
An |.
|
Ai
Aj
Ak
|-...+(-1)n-1
|A1
A2...
An |.
Применим индукцию по n. Для n=2 теорема справедлива (см. ф-лу 1.1). Предположим, что для произвольных подмножеств A1,A2,...,An-1 выполняется равенство
 |
Ai
Aj |+
|
Ai
Aj |+![]() |
Ai
Aj
Ak
|-...+(-1)n-2
|A1
A2...
An |.
|
Ai
Aj
Ak
|-...+(-1)n-2
|A1
A2...
An |.
Применяя эту формулу к сумме
(A1
A2...
An-1)
An
= ,
,
получаем
 |
Ai
Aj
An
|+...+(-1)n-2
|A1
A2...
An
|,
|
Ai
Aj
An
|+...+(-1)n-2
|A1
A2...
An
|,
отсюда мощность объединения n подмножеств A1,A2,...,An множества Х будет равна:

 |
Ai
Aj
| +
|
Ai
Aj
| +
+| Ai Aj Ak |-...+(-1)n-1 |A1 A2... An |.
Пример. В ящике хранятся разноцветные мячи. Известно, что в раскраске 14 мячей присутствует красный, 15 мячей - зелёный, 10 мячей - синий цвет; у 9 мячей - как красный, так и синий, 11 мячей - как красный, так и зелёный, 7 мячей - как синий, так и зелёный цвет; в раскраске 5 мячей присутствуют все три цвета. Сколько мячей в ящике?
Решение. Пусть А, В, С - множества мячей, в раскраске которых присутствует соответственно красный, зелёный и синий цвет. Тогда общее количество мячей составит:
|ABС| = |A| + |B| + |C| - |АВ| - |АC| - |BC| + |ABC| =
= 14 + 15 + 10 - 11 - 9 - 7 + 5 = 17.
Теорема 1.5 (обобщённое правило суммы).
Для покрытия конечного множества A=A1 A2... Am справедливо неравенство
|A| |A1|+|A2|+...+ |Am|. (1.2)
Доказательство проведём методом математической индукции.
При m=2 A=A1A2 и согласно теореме (1.3) имеем
|A| = | A1 A2| = | A1|+| A2| - | A1 A2| |A1|+|A2|.
Предположим, что при m=k неравенство (1.2) верно:
|A| = |A1 A2... Ak | |A1|+|A2|+...+ |Ak|. (1.2,a)
Положим m=k+1 и докажем, что и в этом случае обобщённое правило суммы остаётся верным:
|A|
= |A1
A2...
Ak
Ak+1|
= |(A1
A2...
Ak)
(Ak+1)|
![]() |A1
A2...
Ak|
+ |Ak+1|
-
|A1
A2...
Ak|
+ |Ak+1|
-
- |(A1
A2...
Ak)(Ak+1)|
|A1
A2...
Ak|
+ |Ak+1|![]() |A1|+|A2|+...+
|Ak|+
|Ak+1|.
|A1|+|A2|+...+
|Ak|+
|Ak+1|.
Задача Льюиса Керролла.
В ожесточённом бою 70 из 100 пиратов потеряли один глаз, 75 - одно ухо, 80 - одну руку и 85 - одну ногу. Каково минимальное число потерявших одновременно глаз, ухо, руку и ногу?
Решение. Пусть A1, A2, A3, A4 - множества пиратов, потерявших соответственно глаз, ухо, руку, ногу. Тогда В = (A1A2A3 A4) - это множество пиратов, потерявших одновременно глаз, ухо, руку и ногу.
Множество всех пиратов U можно представить в виде покрытия
![]() ,
,
причём по условию |U|=100.
Используя формулу (1.2), получим
![]() ,
,
откуда
100 (100-70)+(100-75)+(100-80)+(100-85)+|B| ; |B| 10.
Теорема 1.6. Для разбиения конечного множества A=A1 A2... Am, Ai , AiAj=, ij, 1 i, j m справедливо равенство|A| = |A1|+|A2|+...+ |Am|. (правило суммы), которое доказывается аналогично формуле (1.2).
Теорема 1.7. (о мощности прямого произведения).
Пусть A1,A2,...,An - конечные множества и |A1|=m1, |A2|=m2,..., |An|=mn. Тогда мощность множества A1A2...An равна произведению мощностей A1,A2,...,An :
|A1A2...An|
= m1![]() m2
m2![]() ...
...![]() mn.
mn.
Применим индукцию по n.
1. n=2. Пронумеруем элементы множеств B=A1 и C=A2 и составим декартово произведение BC: B={b1,b2,...,bm1}, C={c1,c2,...,cm2},
BC={ (b1,c1), (b1,c2),..., (b1,cm2),
(b2,c1), (b2,c2),..., (b2,cm2),
...
(bm1,c1), (bm1,c2),..., (bm1,cm2)}.
Ясно,
что мощность множества BC
равна m1![]() m2:
m2:
|A1A2
|= m1![]() m2.
(1.3)
m2.
(1.3)
2. n=k.
Предположим, что |A1A2...Ak
| =
m1![]() m2
m2![]() ...
...![]() mk
. (1.3,а)
mk
. (1.3,а)
3. n=k+1.
Докажем, что |A1A2...Ak
Ak+1|
= m1![]() m2
m2![]() ...
...![]() mk.
mk.
![]() mk+1.
mk+1.
|A1A2...Ak
Ak+1|
=|(A1A2...Ak)Ak+1|![]()
=
|A1A2...Ak
|![]() |Ak+1|
|Ak+1|![]() (m1
(m1![]() m2
m2![]() ...
...![]() mk)
mk)![]() mk+1=
m1
mk+1=
m1![]() m2
m2![]() ...
...![]() mk.
mk.
![]() mk+1.
mk+1.
Следствие. Пусть А - конечное множество и |A| = m. Тогда |An| = mn .
Пример.Сколько векторов длиной 3 со значениями компонент 0 или 1 можно составить?
Решение. Эти вектора представляют собой элементы множества B3, где B={0,1}. Общее число векторов с заданными свойствами равно мощности множества B3. Так как |B|=2, то |B3|=23=8.
