Задачи для самостоятельного решения

Задание 1.7. Элементами множеств А, В, С служат числа 1,2,3,...,9. Известно следующее: АВ={1,2}, АВ={1,2,3,6,7,8}, ВС={3,7}, АС={1,2, 3,4,5,7,9}. Найдите множества А, В и С.

Задание 1.8. Определить, какими свойствами обладают бинарные отношения:

а) R={(x,y)/ x+y7; x, y  Z};

б) M - множество прямых на плоскости:

• R={(a,b) / a и b параллельны; a, b  M};

• R={(a,b) / a и b перпендикулярны; a, b  M};

• R={(a,b) / a и b имеют хотя бы одну общую точку; a, b  M};

Конечные графы

Задание 2.1. Каким является и каким не является (полным, эйлеровым, двудольным, гамильтоновым, планарным, деревом) данный неориентированный граф (рисунок 1)? Ответ обосновать.

Решение. Данный граф

• является полным, т.к. любые две его вершины смежные,

• является эйлеровым, т.к. степени всех его вершин чётные,

• не является двудольным, т.к. содержит циклы чётной длины,

• является гамильтоновым, т.к. любой полный граф содержит гамильтонов цикл,

• не является планарным по следствию из теоремы Эйлера,

• не является деревом, т.к. содержит циклы.

Рисунок 1.

Задание 2.2. Подсчитать количество различных неориентированных графов, которые можно построить на 4 помеченных вершинах.

Решение. Подсчитаем количество различных диаграмм, которые можно построить на этих вершинах. Максимальное количество рёбер в графе определяется количеством способов, которыми из 4 вершин можно выбрать две: С₄² = 6. Т.к. для каждого ребра существует две возможности: либо его проводят, либо нет, то количество диаграмм, а значит, и графов, равно 2⁴ = 16.

Задание 2.3. Составить код Прюфера для дерева, изображённого на рисунке 2, а.

Решение.

1. Концевая вершина с самым маленьким номером - 3, а соответствующее ей концевое ребро - (2,3), поэтому принимаем a₁=2 и отсекаем это ребро.

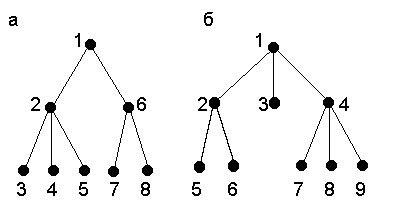
Рисунок 2.

2. Концевая вершина с самым маленьким номером из оставшихся - 4, а соответствующее ей концевое ребро - (2,4). Поэтому принимаем a₂=2 и отсекаем это ребро. Дальше действуем аналогично.

Требуемый вектор имеет вид: (2,2,2,1,6,6).

Задание 2.4. По коду Прюфера восстановить дерево Т: (1, 2, 2, 1, 4, 4, 4). (’’)

Решение. Данный вектор содержит 7 компонент, значит, дерево Т должно иметь 7+2=9 вершин. Выпишем последовательность номеров этих вершин:

1, 2, 3, 4, 5, 6, 7, 8, 9. (’)

1. В (’) находим первое число, которое не содержится в (’’), - 3. Получаем ребро (1,3). Зачёркиваем 1 в (’’), 3 в (’); остаётся:

(2, 2, 1, 4, 4, 4), (’’)

1, 2, 4, 5, 6, 7, 8, 9. (’)

2. Первое число в (’), которое не содержится в (’’), - это 5. Получаем следующее ребро - (2,5). Зачёркиваем 2 в (’’), 5 в (’); остаётся:

(2, 1, 4, 4, 4), (’’)

1, 2, 4, 6, 7, 8, 9. (’)

Повторяя эту процедуру ещё 3 раза, получим рёбра (2,6), (1,2), (4,1), (4,7), (4,8). После этого в последовательности (’) останутся два числа - 4 и 9. Они определяют последнее, восьмое, ребро (4,9). Так как все рёбра известны, восстанавливаем дерево Т, схема которого приведена на рис. 2, б.

Задание 2.5. Построить базисный граф для графа, изображённого на рисунке 3, а.

Решение. Рассуждаем следующим образом:

• удалить ребро (1,2) , так как есть цепь (1,0)+(0,2) ;

• оставить ребро (1,0) с учётом того, что ребро (1,2) уже удалено;

• удалить ребро (3,2) , так как есть цепь (3,0)+(0,2) ;

• оставить ребро (3,0) ;

• удалить ребро (3,4) , так как есть цепь (3,0)+(0,4) ;

• оставить ребро (5,0) ;

• удалить ребро (5,4) , так как есть цепь (5,0)+(0,4) ;

• оставить ребро (0,2) ;

• оставить ребро (0,4) .

Окончательный вариант базисного графа представлен на рисунке 3, б.

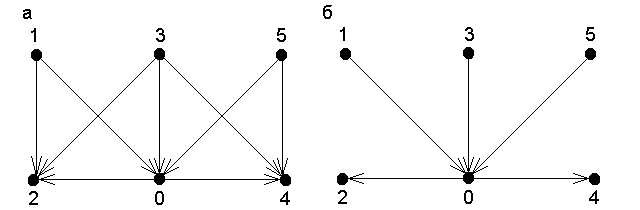
Рисунок 3

Задание 2.6. Доказать, что наибольшее число рёбер у графов, имеющих n вершин и не содержащих треугольников, равно [n²/4].

Решение. Доказательство проводится по индукции  отдельно для чётных и нечётных значений n. Ограничимся чётными.

Для малых значений n утверждение очевидно.

Пусть верно для всех чётных значений n  2p. Докажем это утверждение для не содержащего треугольников графа F с n = 2p+2 вершинами. Выберем в F две смежные вершины  и . Подграф F* = F  {, } содержит 2p вершин и не имеет треугольников, так что, по предположению, в нем, самое большее, [4p²/4] = p² ребер.

В графе F нет вершины, смежной с вершинами  и  одновременно (иначе существовал бы треугольник). Значит, если вершина  смежна с l вершинами графа F*, то вершина  может быть смежна, самое большее, с 2p  l вершинами, следовательно, в F не больше чем p² + l + (2p  l) + 1 = (p+1)² = n ² / 4 = [n ² / 4] вершин.

Задание 2.7. Доказать, что хроматическое число (F) графа F не превышает 1+(F), где (F)  максимальная из степеней вершин.

Решение. Доказательство проводится по индукции.

При n = 1: (F) = 0, (F) = 1. Пусть утверждение верно при n = k. Докажем, что оно верно и для графа F* с k+1-й вершиной.

Удалив одну из вершин  графа F*, получим граф F, для которого, по предположению, (F)  1+(F). Так как (F)  (F*), то (F)  1+(F*).

Вершина  соединена, как максимум, с (F*) другими вершинами. Значит, среди 1+(F*) цветов найдется хотя бы один для правильной раскраски вершины , т.е. (F*)  1+(F*).