2.6. Синусоидальный ток в цепи с последовательным соединением r, l, с

Пусть в цепи рис. 2.10 течет синусоидальный ток c нулевой начальной фазой ():

. (2.33)

с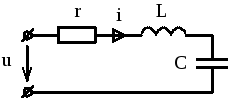

Рис. 2.10

Напряжение на входных зажимах цепи есть также синусоидальная функция времени:

. (2.34)

где , – неизвестные пока амплитуда и начальная фаза входного напряжения.

Согласно второму закону Кирхгофа

. (2.35)

Учтем, что напряжение на сопротивлении совпадает по фазе с током i, напряжение на индуктивности опережает ток на угол , а напряжение на емкости отстает от тока на угол . Тогда

,

или

. (2.36)

Обозначим

– входное реактивное сопротивление цепи.

Тогда выражение (2.36) принимает вид

. (2.37)

Из тригонометрии известно, что

, (2.38)

где.

Тогда входное напряжение u можно записать в виде

, (2.39)

где . (2.40)

Отметим, что реактивное сопротивление индуктивности и реактивное сопротивление емкости всегда положительны, а входное реактивное сопротивление цепи может быть как положительным, так и отрицательным. Если x > 0, то угол сдвига фаз положителен () и входное напряжение опережает ток. Говорят: ”Цепь имеет активно-индуктивный характер”. Если x < 0, то угол сдвига фаз отрицателен () и входное напряжение отстает от тока. Говорят: ”Цепь имеет активно-емкостный характер”.

Обозначим

, (2.41)

где – полное сопротивление цепи.

Выражение (2.41) позволяет построить так называемый треугольник сопротивлений (рис. 2.11).

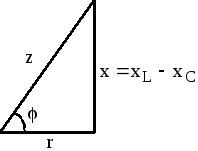
Рис. 2.11

Очевидные соотношения между сторонами прямоугольного треугольника определяют еще одну форму связи между полным, активным и реактивным сопротивлениями:

, (2.42)

. (2.43)

Сравнивая левую и правую части уравнения (2.39), получим

. (2.44)

Аналогичное соотношение для действующих значений тока и напряжения имеет вид

. (2.45)

Выражения (2.44) и (2.45) представляют собой закон Ома для амплитудных (действующих) значений входного напряжения и тока цепи.

Если умножить все стороны треугольника сопротивлений на действующее значение тока, получим так называемый треугольник напряжений (рис. 2.12).

Катеты треугольника напряжений получили название:

– активная составляющая входного напряжения,

– реактивная составляющая входного напряжения.

Очевидно, что для треугольника напряжений справедлива формула

. (2.46)

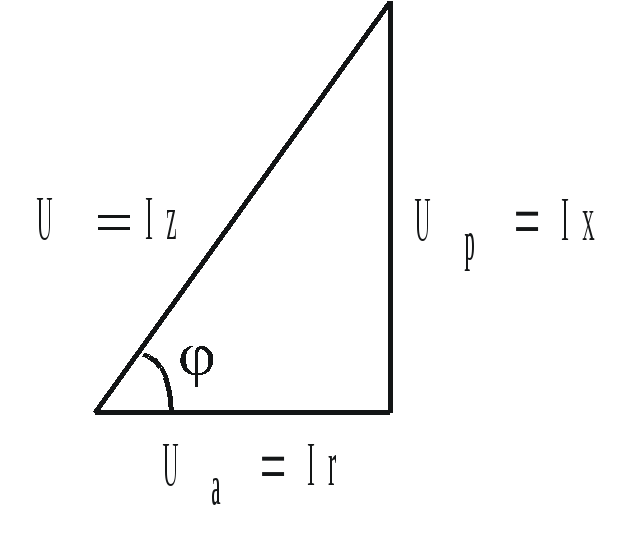
Рис. 2.12

2.7. Синусоидальный ток в цепи с параллельным соединением r, l, c

с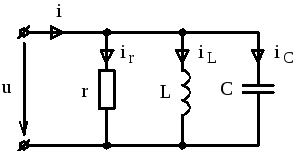

Рис. 2.13

Пусть к цепи рис. 2.13 приложено синусоидальное напряжение c нулевой начальной фазой ():

. (2.47)

Входной ток i есть также синусоидальная функция времени:

. (2.48)

где – неизвестные пока амплитуда и начальная фаза входного тока.

Согласно первому закону Кирхгофа

. (2.49)

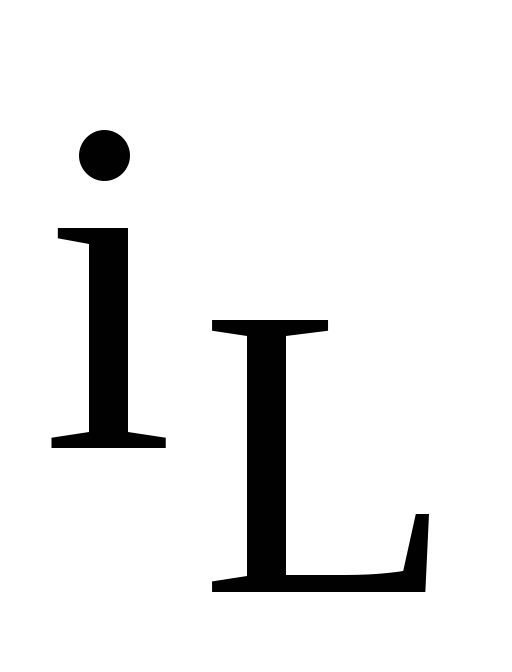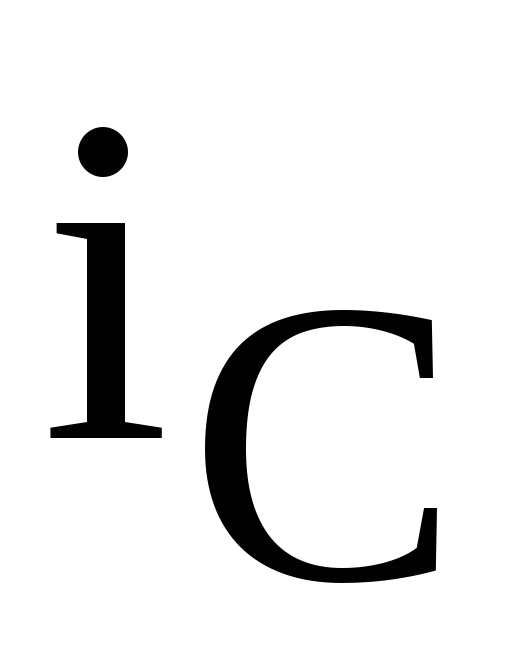Учтем, что ток в сопротивлении совпадает по фазе с напряжением u, ток в индуктивности отстает от напряжения на угол , а ток в емкости опережает напряжение на угол . Тогда

, (2.50)

или

. (2.51)

Обозначим

– входная реактивная проводимость цепи.

Тогда с учетом (2.38) получим

, (2.52)

где . (2.53)

Обозначим

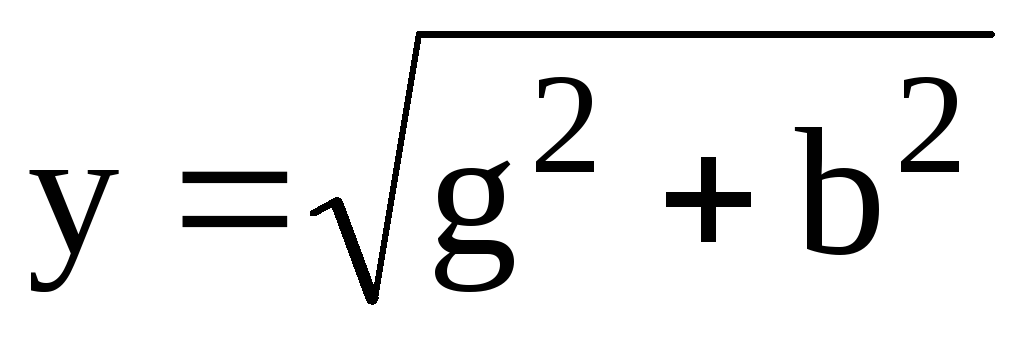, (2.54)

где у – полная проводимость цепи.

Выражение (2.54) позволяет построить так называемый треугольник проводимостей (рис. 2.14).

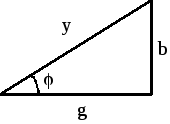
Рис. 2.14

Очевидные соотношения между сторонами прямоугольного треугольника определяют еще одну форму связи между полной, активной и реактивной проводимостями:

, (2.55)

. (2.56)

Сравнивая левую и правую части (2.52), получим

. (2.57)

Аналогичное соотношение для действующих значений тока и напряжения имеет вид

. (2.58)

Если умножить все стороны треугольника проводимостей на действующее значение напряжения, получим так называемый треугольник токов (рис. 2.15).

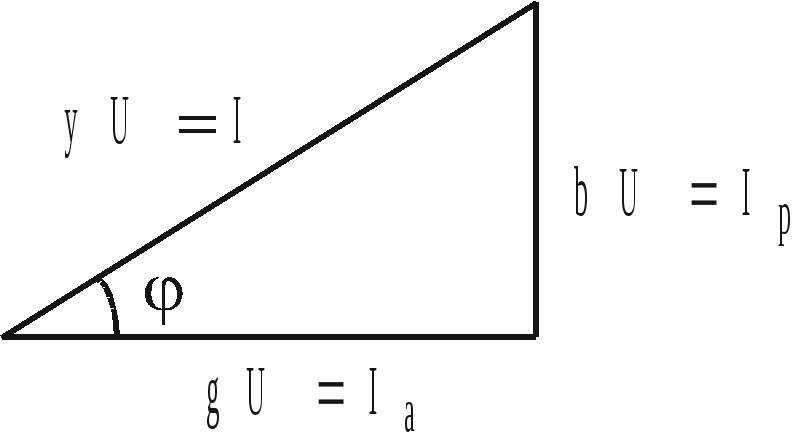
Рис. 2.15

Катеты треугольника токов получили название:

– активная составляющая входного тока,

– реактивная составляющая входного тока.

Очевидно, что для треугольника токов справедлива формула

. (2.59)