1.4. Основные определения, относящиеся к электрической цепи

Условное графическое изображение электрической цепи называется электрической схемой. Она показывает, как осуществляется соединение элементов электрической цепи.

В электрической цепи выделяют ветви, узлы и контуры. Ветвь – это участок электрической цепи, образованный одним или несколькими последовательно включенными элементами, по которым течет один и тот же ток. Напомним, что условные положительные направления токов выбираются произвольно и указываются стрелками.

Так, цепь на рис. 1.16 содержит три ветви. Первая ветвь образована элементами , вторая – и , и третья – одним элементом .

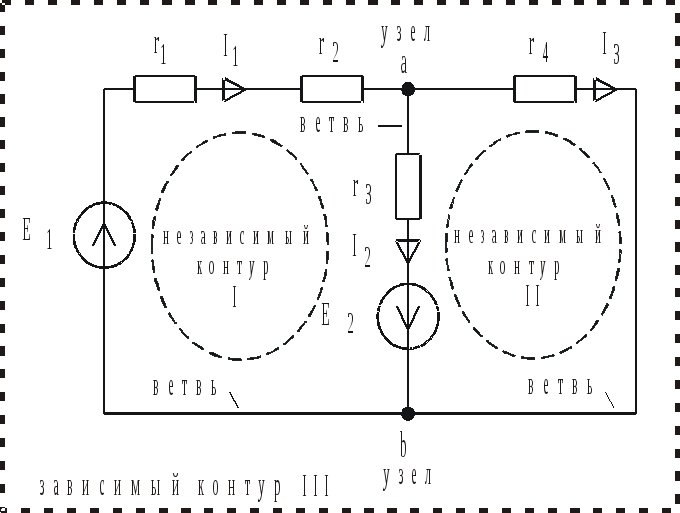
Рис. 1.16

Узел – это место соединения трех и более ветвей. В цепи рис. 1.16 два узла – а и b.

Любой замкнутый путь, проходящий по нескольким ветвям, называется контуром. В цепи рис. 1.16 три контура. Первый образован элементами , второй – 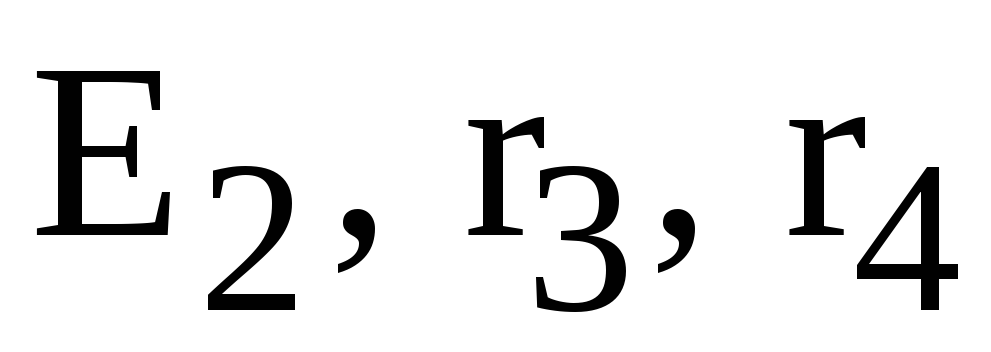, а третий – .

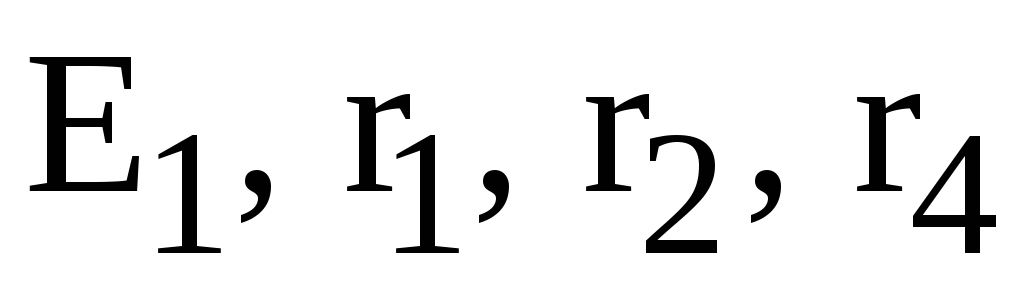Все контуры в электрической цепи можно разделить на независимые и зависимые. Контуры называются независимыми, если каждый из них содержит хотя бы одну ветвь, не вошедшую во все остальные. В противном случае контуры называются зависимыми.

Поскольку общее количество контуров в цепи всегда больше числа независимых, то независимые контуры выбирают произвольно – см. рис. 1.16. Здесь первый контур содержит ветвь с элементами , не вошедшую во второй контур. В свою очередь, второй контур содержит ветвь с элементом , не вошедшую в первый контур. Все ветви третьего контура входят в первый и второй контуры, и поэтому третий является зависимым по отношению к первым двум.

1.5. Закон Ома для участка цепи, содержащего эдс

Позволяет определить ток по известным величинам ЭДС и напряжения на концах этого участка.

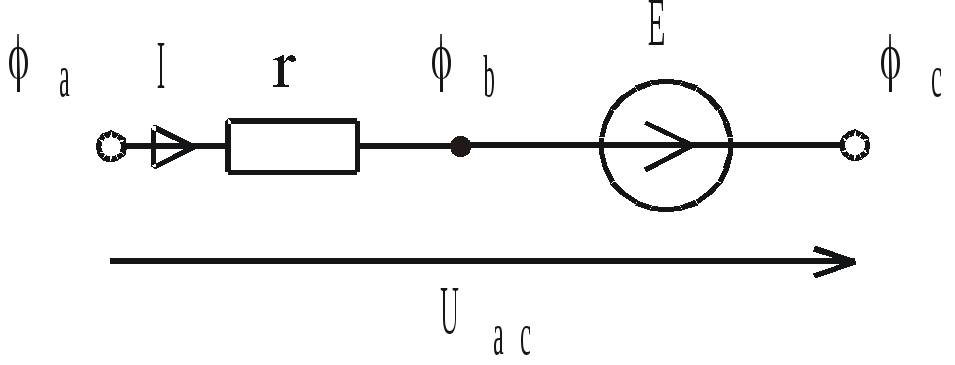
Рис. 1.17

Дано: .

Определить I.

Выразим потенциалы точек а и с рассматриваемого участка цепи рис. 1.17:

,

.

Тогда напряжение на зажимах а, с

.

Отсюда искомый ток

. (1.17)

Отметим, что в рассматриваемом случае (рис. 1.17) направления тока и источника ЭДС совпадают, что отражается знаком « + » перед ЭДС Е в формуле (1.17).

Если направления тока и источника ЭДС противоположны (рис. 1.18), то закон Ома принимает вид

. (1.18)

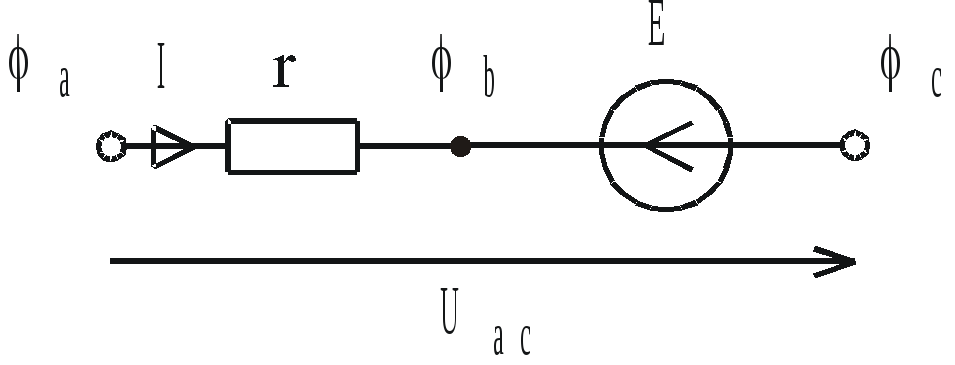
Рис. 1.18

1.6. Законы Кирхгофа

Первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю

. (1.19)

При этом токам, направленным к узлу, приписывается какой-либо один знак (например « + »), а от узла – противоположный.

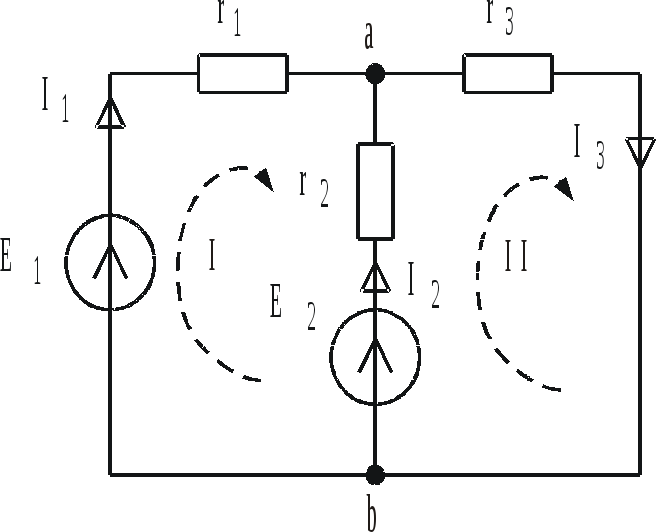
Рис. 1.19

Так, для узла а цепи рис. 1.19 первый закон Кирхгофа имеет вид

.

Второй закон Кирхгофа: алгебраическая сумма ЭДС в любом замкнутом контуре равна алгебраической сумме падений напряжений на остальных элементах этого контура:

. (1.20)

Предварительно необходимо произвольно выбрать направление обхода контура, например, по часовой стрелке (см. рис. 1.19). Если направления ЭДС и условные положительные направления напряжений на элементах контура совпадают с выбранным направлением обхода контура, то такие ЭДС и напряжения записываются со знаком « + », в противном случае – « – ».

Отметим, что условное положительное направление напряжения на пассивных элементах цепи совпадает с условным положительным направлением тока в них.

С учетом вышеизложенного запишем второй закон Кирхгофа для первого контура цепи рис. 1.19:

.

При его записи учитывалось, что:

а) направление совпало с направлением обхода контура, а направление противоположно направлению обхода;

б) направление тока в сопротивлении совпадает с направлением обхода контура, а направление тока в сопротивлении противоположно направлению обхода.

Аналогично для второго контура цепи рис. 1.19 можно записать

.