1.2. Условные положительные направления тока и напряжения

Для расчета электрических цепей необходимо учитывать направления токов и напряжений. Направление тока характеризуется знаком тока. Понятия «положительный ток» и «отрицательный ток» имеют смысл, если только сравнивать направление тока в проводнике с некоторым заранее выбранным ориентиром – так называемым положительным направлением. Его выбирают произвольно и указывают стрелкой.

Если в результате расчета тока, выполненного с учётом принятого положительного направления, ток имеет знак плюс (i>0), то это значит, что его фактическое направление совпадает с выбранным положительным направлением. В противном случае, когда ток отрицателен (i<0) – противоположно выбран­ному.

Рассмотрим условные положительные направления напряжения и тока в отдельных пассивных элементах цепи.

1.2.1. Сопротивление

Пусть через участок цепи с сопротивлением r проходит ток i (рис. 1.6).

Рис. 1.6

Разность электрических потенциалов точек 1 и 2 представляет собой напряжение на данном участке (сопротивлении):

. (1.9)

Численно напряжение равно работе, совершаемой силами электрического поля по перемещению единичного положительного заряда из точки 1 в точку 2.

Для напряжения, так же как и для тока, произвольно выбирается положительное направление. Обычно оно совпадает с направлением тока (указывают стрелкой) – рис. 1.6.

В рассматриваемом случае

,

откуда

,

т. е. ток течет от большего потенциала к меньшему.

По закону Ома напряжение на сопротивлении

.

1.2.2. Индуктивность

На основании закона электромагнитной индукции, всякое изменение потокосцепления самоиндукции вызывает ЭДС самоиндукции

. (1.10)

Величина

(1.11)

называется напряжением на индуктивности. Положительное направление совпадает с положительным направлением тока (рис. 1.7).

Рис. 1.7

Из выражения (1.11) можно определить ток как

. (1.12)

1.2.3. Емкость

При изменении напряжения, приложенного к пластинам конденсатора, изменяется и электрический заряд . Изменение заряда, в свою очередь, приводит к возникновению тока в ветви с емкостью

. (1.13)

Положительное направление напряжения на емкости совпадает с положительным направлением тока (рис. 1.8).

с

Рис. 1.8

Из выражения (1.13) можно определить напряжение как

. (1.14)

1.3. Источники эдс и тока

В теории электрических цепей пользуются идеализированными источниками электрической энергии: источником ЭДС и источником тока. Им приписывают следующие свойства.

Идеальным источником ЭДС называется активный элемент с двумя выводами (рис. 1.9), напряжение на которых не зависит от величины тока, проходящего через источник. Внутреннее сопротивление идеального источника ЭДС равно нулю.

Упорядоченное перемещение положительных зарядов внутри источника от клеммы « – » к клемме « + » происходит за счет присущих источнику сторонних сил. Величина, численно равная работе, совершаемой сторонними силами при перемещении единичного положительного заряда от зажима « – » к зажиму « + », называется ЭДС источника и обозначается Е.

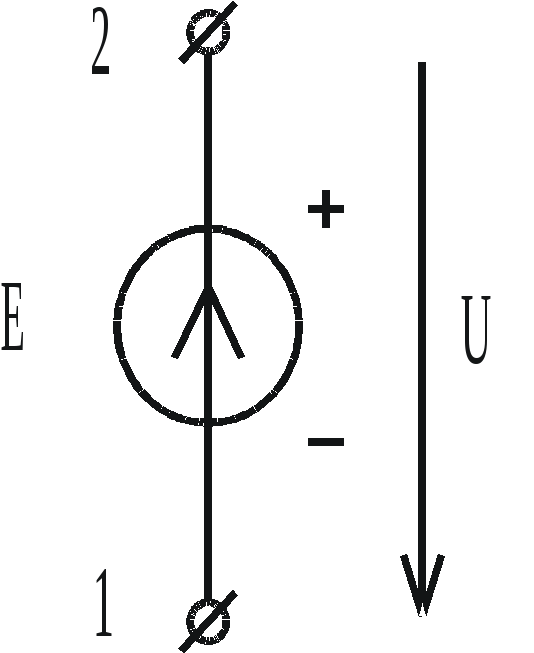
Рис. 1.9

При подключении нагрузки (сопротивление r, рис. 1.10) к источнику возникает замкнутый путь для протекания тока, который направлен вне источника от клеммы « + » к клемме « – ».

Рис. 1.10

Очевидно, что работа, совершаемая электрическим полем по перемещению единичного положительного заряда по участку цепи с сопротивлением, равна работе, совершаемой сторонними силами внутри источника по перемещению того же заряда от зажима « – » к зажиму « + ». Следовательно, напряжение на зажимах источника ЭДС равно самой ЭДС, т.е.

.

Отсюда

.

Таким образом, стрелка внутри источника ЭДС указывает на направление возрастания потенциала. При этом потенциал зажима « + » больше потенциала зажима « – » на величину самой ЭДС Е.

Величину тока в цепи рис. 1.10 можно определить по закону Ома

.

Поскольку у идеального источника E = const, то при уменьшении нагрузки r ток будет неограниченно возрастать и в пределе стремится к бесконечности. Поэтому идеальный источник ЭДС является источником бесконечной мощности (теоретическое понятие).

В действительности при замыкании накоротко зажимов реального источника ЭДС ток может принимать только конечное значение. Схема замещения реального источника ЭДС конечной мощности состоит из двух идеальных элементов, включенных последовательно: идеального источника ЭДС и сопротивления r, которое ограничивает мощность, отдаваемую во внешнюю цепь (рис. 1.11). В данном случае сопротивление r называется внутренним сопротивлением реального источника ЭДС.

Рис. 1.11

Для источника рис. 1.11 справедливо:

,

,

тогда напряжение на зажимах реального источника ЭДС

. (1.15)

Вольт-амперная характеристика источника ЭДС, построенная по уравнению (1.15), называется внешней (рис.1.12).

Рис. 1.12

Идеальным источником тока называется активный элемент с двумя выводами (рис. 1.13), ток которого J не зависит от напряжения на его зажимах. Внутреннее сопротивление идеального источника тока бесконечно велико.

При подключении нагрузки (сопротивление r, рис. 1.13) к источнику возникает замкнутый путь для протекания тока I. Указанные выше свойства источника тока приводят к тому, что ток в ветви, куда включен источник тока (в рассматриваемом случае – в одноконтурной цепи), всегда равен току самого источника: I = J.

Рис. 1.13

По мере увеличения сопротивления r, подключенного к идеальному источнику тока, напряжение на его зажимах неограниченно возрастает и в пределе стремится к бесконечности. Поэтому идеальный источник тока является источником бесконечной мощности (теоретическое понятие). Схема замещения реального источника тока конечной мощности состоит из двух элементов, включенных параллельно: идеального источника тока и сопротивления r, которое ограничивает мощность, отдаваемую во внешнюю цепь (рис. 1.14).

Рис. 1.14

Напряжение на зажимах реального источника тока

. (1.16)

Вольт-амперная характеристика источника тока, построенная по уравнению (1.16), приведена на рис.1.15.

Рис. 1.15