4.1.3. Взаимные преобразования “треугольник - звезда”,

“звезда - треугольник”

В ряде случаев сложную электрическую цепь можно упростить путем преобразования треугольника сопротивлений в эквивалентную звезду и наоборот (рис. 4.4).

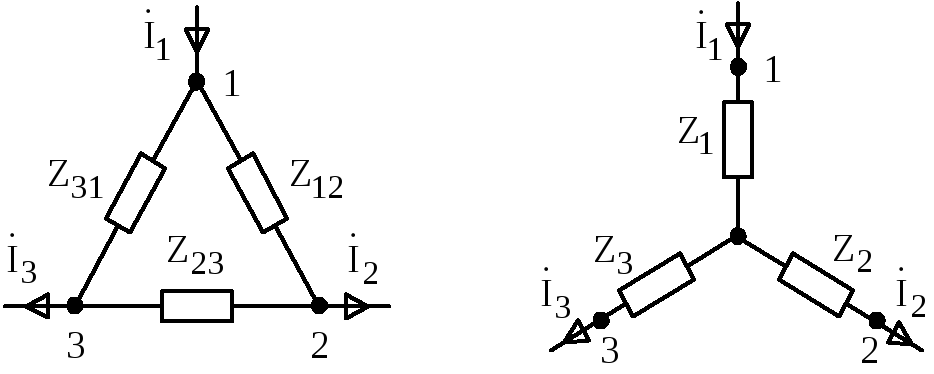
Рис. 4.4

При этом токи и напряжения остальной части цепи должны остаться неизменными.

Формулы преобразования имеют вид:

а) треугольник – звезда

, (4.9)

, (4.10)

; (4.11)

б) звезда – треугольник

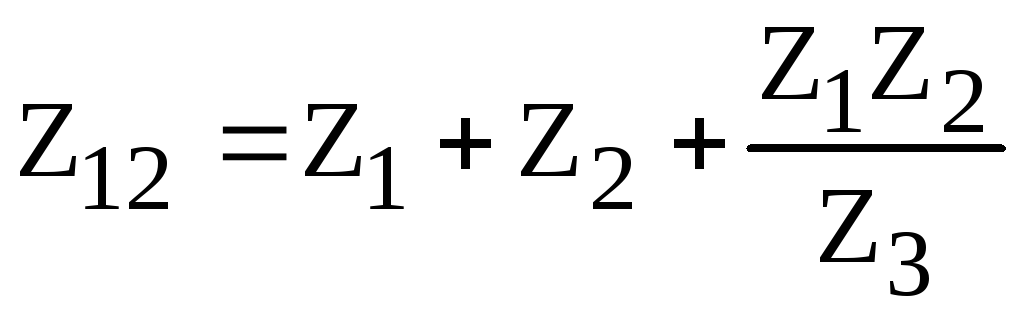, (4.12)

, (4.13)

. (4.14)

Рассмотрим пример расчета цепи рис. 4.5 методом преобразования.

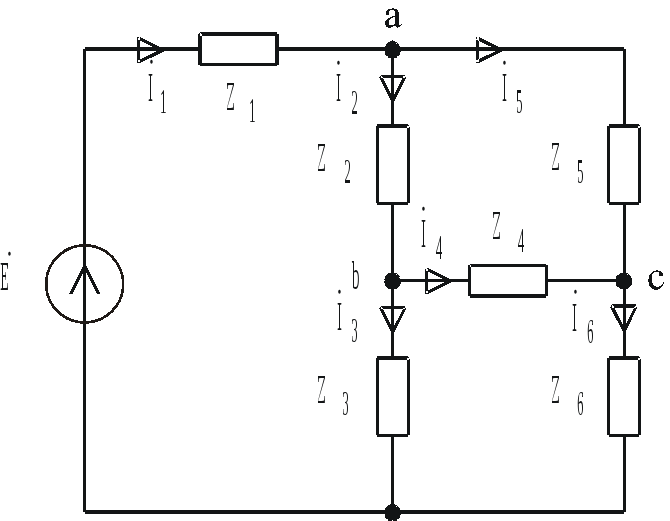
Рис. 4.5

Проведем преобразование треугольника сопротивлений , , в эквивалентную звезду (рис. 4.6):

,

,

.

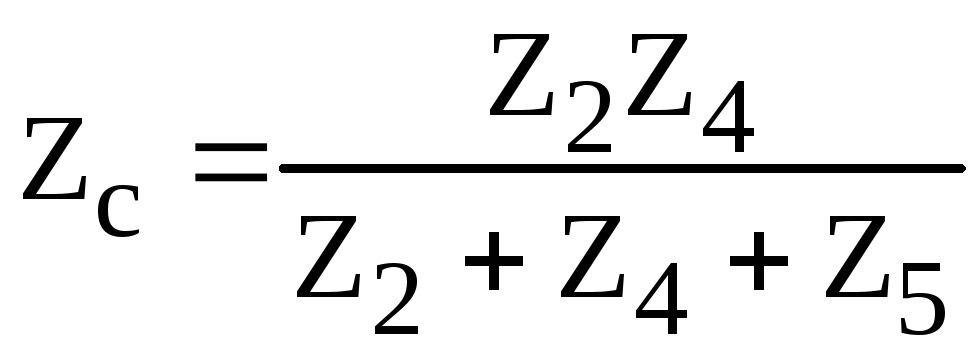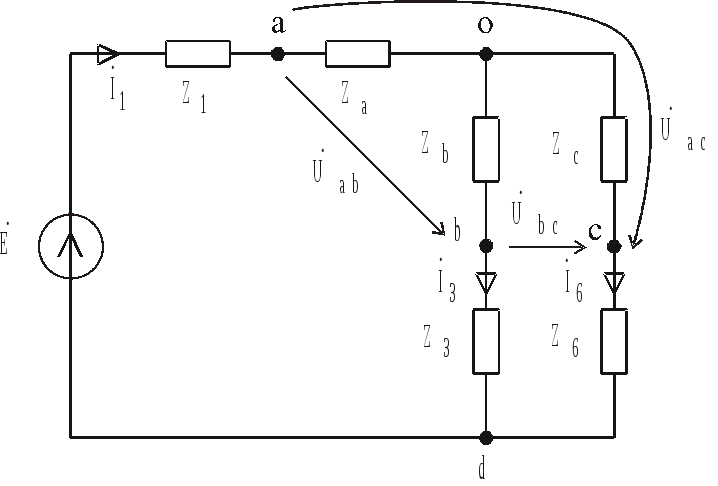
Рис. 4.6

Ветви схемы рис. 4.6 содержат последовательно включенные сопротивления ( и , и , и ), эквивалентные преобразования которых приводят к цепи рис. 4.7.

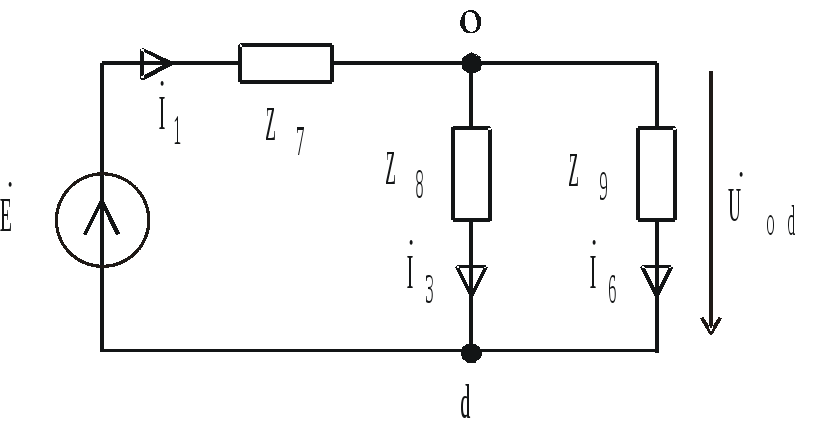
Рис. 4.7

Сопротивления , и (рис. 4.7) определяют по формулам:

,

,

.

На следующем этапе преобразуют параллельно включенные сопротивления и в одно эквивалентное (рис. 4.8):

.

На завершающем этапе эквивалентных преобразований последовательно включенные сопротивления и (рис. 4.8) заменяют одним эквивалентным (рис. 4.9):

.

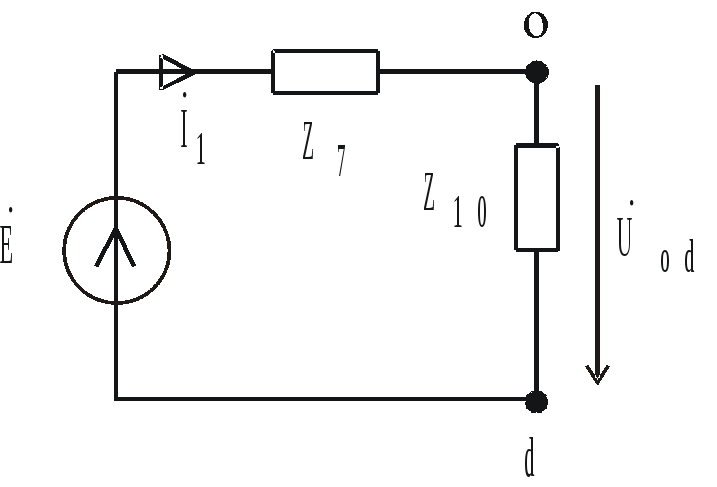
Рис. 4.8

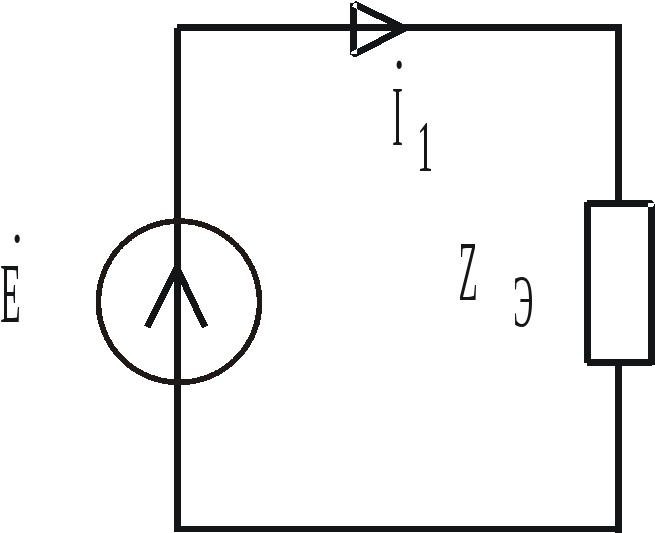
Рис. 4.9

Таким образом, сложная разветвленная цепь рис. 4.5 путем ряда преобразований приведена к простейшей одноконтурной (рис. 4.9), содержащей одно эквивалентное сопротивление . Достоинство полученной схемы – простота определения тока:

.

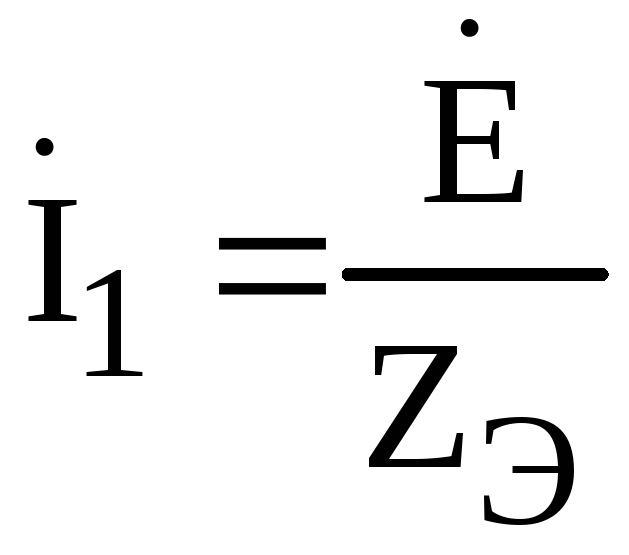Расчет токов , будем осуществлять с учетом того обстоятельства, что напряжения между точками o и d () в схемах рис. 4.7 и рис. 4.8 одинаковы. Для цепи рис. 4.8 справедливо

.

Тогда (схема рис. 4.7)

,

.

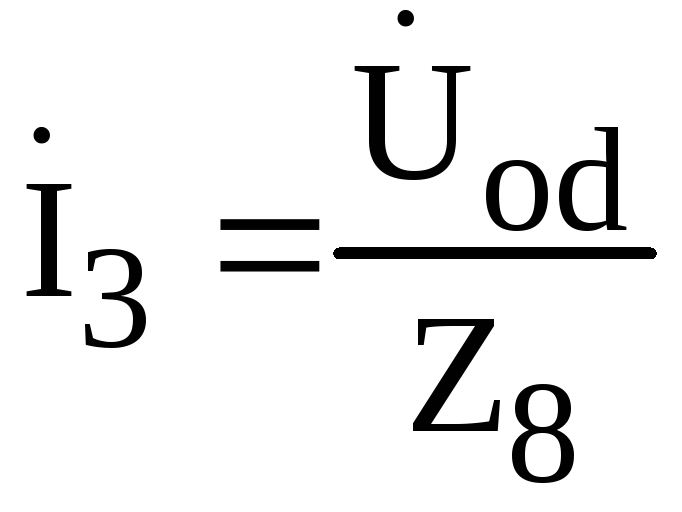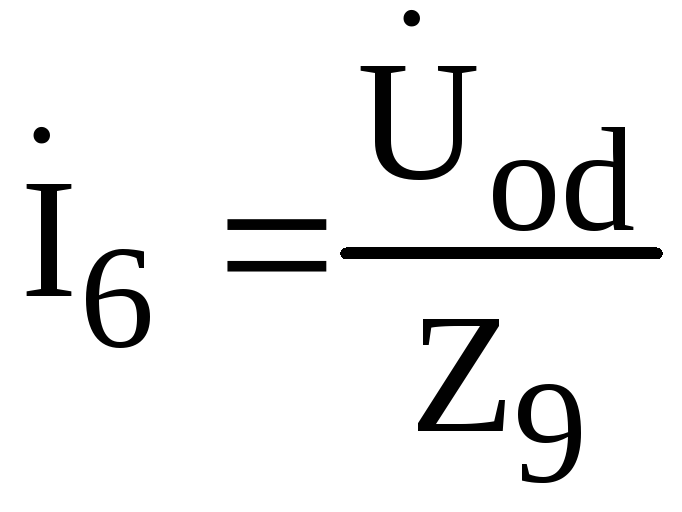Для расчета токов 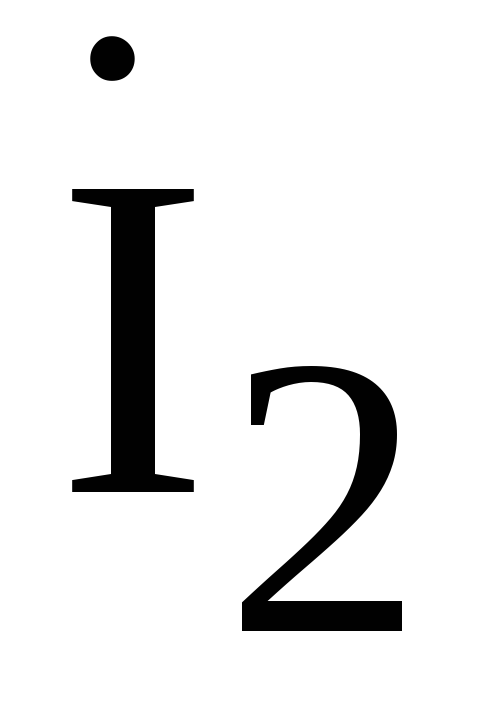, , в ветвях треугольника (рис. 4.5) найдем напряжения , , в цепи рис. 4.6:

,

,

.

Тогда (схема рис. 4.5)

,

,

.

4.2. Метод законов Кирхгофа

Расчёт линейных электрических цепей методом законов Кирхгофа сводится к составлению и решению систем алгебраических уравнений относительно неизвестных токов.

Пусть цепь содержит в качестве источников электрической энергии источники ЭДС. Так как число неизвестных токов равно числу ветвей n этой цепи, то система алгебраических уравнений должна иметь n-й порядок.

Обозначим k – число узлов цепи. Из принципа непрерывности токов следует, что число линейно независимых уравнений, которые можно составить по первому закону Кирхгофа, равно (k - 1). Недостающие уравнения, количество которых равно [n – (k – 1)], составляются по второму закону Кирхгофа для независимых контуров.

Рассмотрим в качестве примера расчёт токов в схеме рис. 4.10, которая содержит n=6 ветвей, k=4 узла и 3 независимых контура.

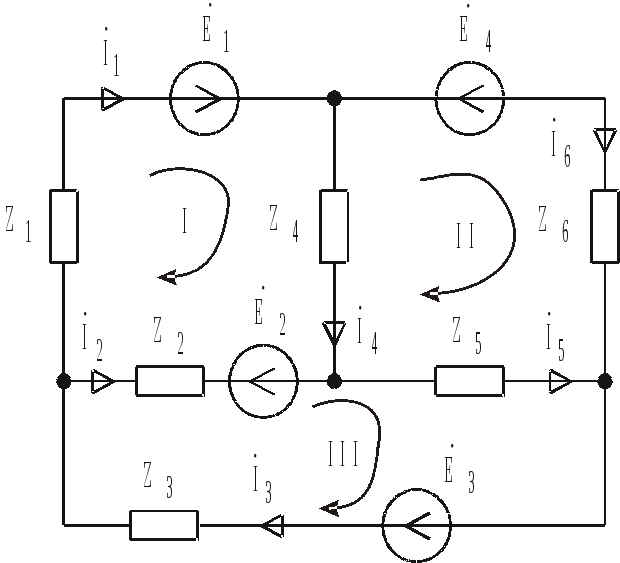
Рис. 4.10

Выберем произвольно направление токов в ветвях и направление обхода независимых контуров. Первые три уравнения (4 – 1 = 3) запишем по первому закону Кирхгофа, а оставшиеся три (6 – 3 = 3) – по второму закону Кирхгофа.

Пусть цепь наряду с источниками ЭДС содержит m источников тока. Так как токи в ветвях с источниками тока равны токам этих источников, то число неизвестных токов уменьшается до величины (n – m). Однако в цепи появляются новые неизвестные величины – напряжения на зажимах источников тока, количество которых равно m. Поэтому общее количество неизвестных величин в цепи остается прежним, равным n.

Изложенные обстоятельства обусловливают возможность составления двух вариантов систем уравнений по законам Кирхгофа.

1. Если по условию задачи необходимо найти токи в ветвях и не требуется определять напряжения на зажимах источников тока, достаточно составить систему из (n – m) уравнений относительно неизвестных токов. В этой системе по-прежнему (k-1) уравнений составляется по первому закону Кирхгофа, а по второму – [n – m – (k – 1)]. Естественно, что при записи уравнений по второму закону Кирхгофа выбираются независимые контуры, не содержащие источников тока.

2. Если по условию задачи необходимо найти токи в ветвях и напряжения на зажимах источников тока, необходимо составить систему из n уравнений. В ней (k-1) уравнение составляется по первому закону Кирхгофа и [n – (k – 1)] уравнений – по второму закону для всех независимых контуров.

Рассмотрим в качестве примера расчёт цепи рис. 4.11. Если требуется определить только токи в ее ветвях, то система уравнений имеет вид:

Данная система не содержит уравнение для независимого контура III, содержащего источник тока .

Рис. 4.11

Если в цепи рис. 4.11 необходимо рассчитать токи в ветвях и напряжение на зажимах источника тока , то система уравнений имеет вид