3.2. Векторная диаграмма
Векторной диаграммой называется совокупность векторов на комплексной плоскости, изображающих синусоидальные функции времени одинаковой частоты и построенных с соблюдением их взаимной ориентации по фазе.
Как
было показано выше, в основе комплексного
метода лежит замена синусоидальных
функций вращающимися векторами (рис.
3.3). Однако попытка нарисовать вектор,
вращающийся на комплексной плоскости
в течение какого-либо интервала времени,
приведет к появлению на ней зачерненной
окружности (сектора). Поэтому на векторных
диаграммах условились рисовать векторы
для момента времени
(т.е. по сути делать “мгновенную
фотографию” вращающихся векторов при
)
– рис. 3.6.
Рис. 3.6
Векторные
диаграммы дают наглядное представление
о фазовых соотношениях между токами и
напряжениями на отдельных участках
электрической цепи. Так, в рассматриваемом
примере рис. 3.6 напряжение опережает
ток. Это приводит к тому, что на векторной
диаграмме (рис. 3.6) вектор напряжения
повернут в положительном направлении
(т.е. против часовой стрелки) относительно
вектора тока, причем угол между
рассматриваемыми векторами меньше
.
Учет этих двух факторов (поворот одного
вектора относительно другого в
положительном направлении и угол между
векторами, меньший
)
позволяет с помощью векторных диаграмм
легко определять опережающие (отстающие)
напряжения и токи.
Так,
на векторной диаграмме рис. 3.7 ток
опережает ток
.
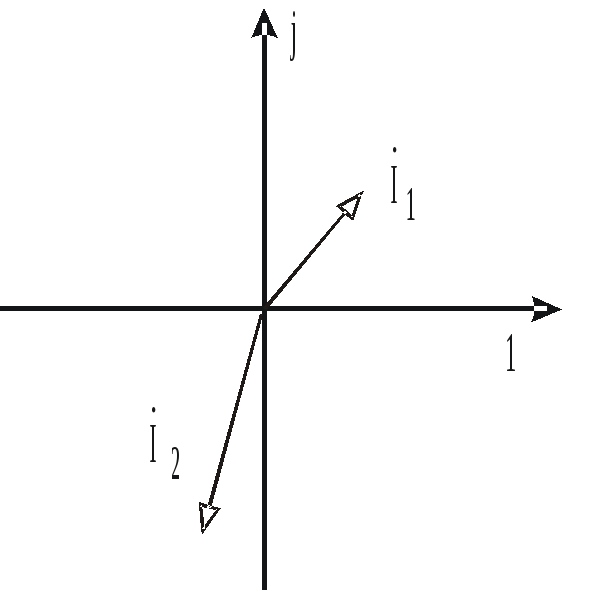
Рис. 3.7
С помощью векторных диаграмм можно производить сложение и вычитание синусоидальных функций времени, что позволяет осуществлять геометрическую интерпретацию законов Кирхгофа на комплексной плоскости.
Рассмотрим в качестве примера сложение двух синусоидальных токов.
Дано:
.
Определить
.
Отложим
на комплексной плоскости векторы
и
(рис.
3.8).
Рис. 3.8
Геометрическая
сумма векторов
,
дает комплексную амплитуду искомого
тока
.
Длина полученного вектора равна амплитуде
искомого тока
,
а угол между действительной осью и
суммарным вектором равен начальной
фазе
тока
.
Отметим, что в рассматриваемом примере
ток
опережает токи
и
.
Рассмотрим векторные диаграммы токов и напряжений для отдельных пассивных элементов цепи.
3.2.1. Сопротивление
Пусть
через резистор
течет ток
(рис. 3.9).
Рис. 3.9
Напряжение
на сопротивлении
(или для комплексных действующих значений
)
совпадает по фазе с током. Отсюда следует,
что на векторной диаграмме векторы тока
и напряжения расположены под одним и
тем же углом
к действительной оси (рис. 3.10).
Рис. 3.10
3.2.2. Индуктивность
Пусть
через индуктивность
течет ток
(рис. 3.11).
Рис. 3.11
Напряжение
на индуктивности
(или для комплексных действующих значений
)
опережает ток на угол
.
Соответственно и на векторной диаграмме
вектор напряжения опережает вектор
тока на
(рис. 3.12).
Рис. 3.12
3.2.3. Емкость
П
усть
через емкость с течет ток
(рис. 3.13).
с
Рис. 3.13
Напряжение
на емкости
(или для комплексных действующих значений
)
отстает от тока на угол
.
Соответственно и на векторной диаграмме
вектор напряжения отстает от вектора
тока на
(рис. 3.14).
Рис. 3.14
3.2.4. Топографическая векторная диаграмма
Частным случаем векторной диаграммы является топографическая векторная диаграмма, на которой откладываются комплексные потенциалы отдельных точек цепи по отношению к одной точке, потенциал которой принят равным нулю. Порядок расположения векторов на топографической диаграмме соответствует порядку расположения элементов цепи.
Отметим, что по определению топографическая диаграмма используется как геометрическая интерпретация второго закона Кирхгофа (т.е. на ней откладываются векторы напряжений).
Существуют два способа построения топографической диаграммы.
I способ.
Строят, двигаясь по элементам цепи в направлении, совпадающем с направлением тока. В этом случае вектор напряжения на диаграмме и соответствующая стрелка напряжения на схеме ориентированы одинаково – от высшего потенциала к низшему.
Рассмотрим в качестве примера цепь рис. 3.15.
с
Рис. 3.15
Отложим
на комплексной плоскости вектор тока
под углом
к
действительной оси (рис. 3.16).
Рис. 3.16
Обозначим промежуточные точки рассматриваемой цепи буквами a, b, d, h. Обход контура будем совершать по направлению тока (т. е. по часовой стрелке), принимая комплексный потенциал точки а равным нулю. Последнее приводит к тому, что на комплексной плоскости точка а расположена в начале координат (рис. 3.16).
При
движении в выбранном направлении по
элементам цепи из точки а (рис. 3.15) первым
элементом цепи является емкость с.
Откладываем на топографической диаграмме
из точки а вектор напряжения на емкости
,
который отстает от тока на угол
(рис. 3.17). Конец вектора
определяет
величину комплексного потенциала точки
b
на векторной диаграмме.
Следующий
элемент цепи при движении по направлению
тока – сопротивление r
(см. рис. 3.15). Откладываем на топографической
диаграмме вектор напряжения на
сопротивлении
,
который совпадает по направлению с
вектором тока
(рис. 3.18).
Рис. 3.17
Рис. 3.18
Конец
вектора
определяет величину комплексного
потенциала точки d
на векторной диаграмме.
Следующий
элемент цепи при движении по направлению
тока – индуктивность L
(см. рис. 3.15). Откладываем на топографической
диаграмме вектор напряжения на
индуктивности
,
который опережает вектор тока
(рис. 3.19). Конец вектора
определяет величину комплексного
потенциала точки h
на векторной диаграмме.
Разность
потенциалов точек a
и h
равна входному напряжению цепи
(см. рис. 3.15). Для получения соответствующего
вектора на диаграмме необходимо соединить
прямой линией точки a
и h.
Конец вектора
на диаграмме должен быть направлен так
же, как и стрелка напряжения на схеме,
– от точки а к точке h
(рис. 3.20).
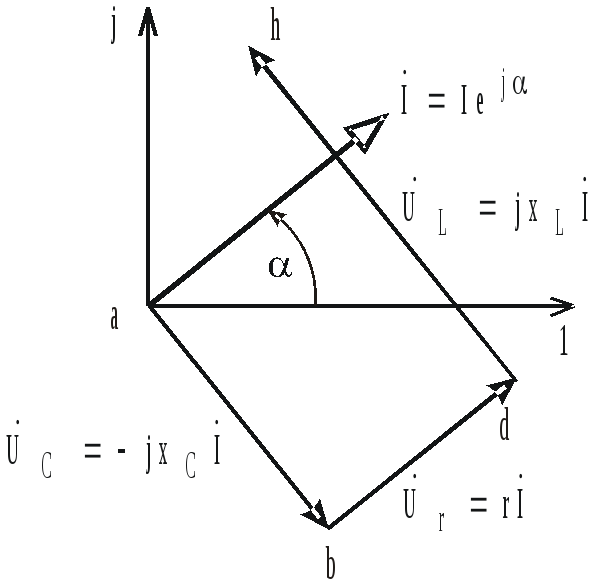
Рис. 3.19
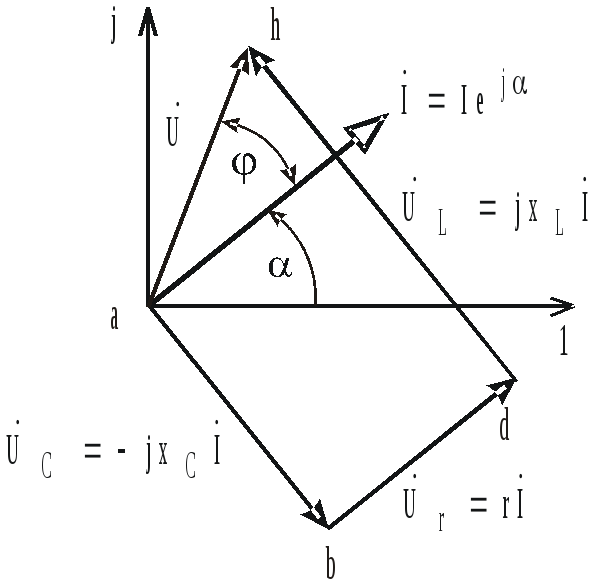
Рис. 3.20
Угол
между векторами напряжения и тока (рис.
3.20) равен углу сдвига фаз
.
В данном случае входное напряжение
опережает ток и цепь имеет активно-индуктивный
характер.
2 способ.
Строят, двигаясь по элементам цепи в направлении, противоположном направлению тока. В этом случае вектор напряжения на диаграмме направлен от точки низшего потенциала к точке высшего потенциала. Это же напряжение на схеме указывается стрелкой противоположного направления.
Итак, будем совершать обход цепи рис. 3.21 в направлении, противоположном току, принимая комплексный потенциал точки h равным нулю.
с
Рис. 3.21
Последнее приводит к тому, что на комплексной плоскости точка h расположена в начале координат (рис. 3.22).
Рис. 3.22
При
движении в выбранном направлении по
элементам цепи из точки h
(рис. 3.21) первым элементом цепи является
индуктивность L.
Откладываем на топографической диаграмме
из точки h
вектор напряжения на индуктивности
,
который опережает вектор тока
(рис. 3.23). Конец вектора
определяет величину комплексного
потенциала точки d
на векторной диаграмме.
Рис. 3.23
Продолжая движение в выбранном направлении по элементам цепи и осуществляя аналогичные построения, получим результирующую топографическую диаграмму рис. 3.24.
Рис. 3.24
Сравнение векторных диаграмм рис. 3.20 и 3.24, построенных двумя способами, показывает их полную идентичность (векторы одноименных величин на диаграммах имеют одинаковое направление). Область преимущественного использования второго способа – трехфазные цепи.