2.9. Баланс мощностей в цепи синусоидального тока

На основании закона сохранения энергии:

а) активная мощность источников должна равняться активной мощности приемников:

, (2.68)

или

; (2.69)

б) реактивная мощность источников должна равняться реактивной мощности приемников

, (2.70)

или

. (2.71)

Для индуктивностей произведение входит в правую часть (2.71) со знаком « + », для емкостей – со знаком « – ».

3. Символический (комплексный) метод расчета цепей синусоидального тока

В его основе лежат замена синусоидальных функций вращающимися векторами и комплексные числа. Это позволяет осуществить переход от интегро-дифференциальных уравнений для мгновенных значений токов и напряжений к алгебраическим уравнениям, составленным относительно комплексов токов и напряжений.

Комплексные числа отображаются в виде векторов на комплексной плоскости (рис. 3.1).

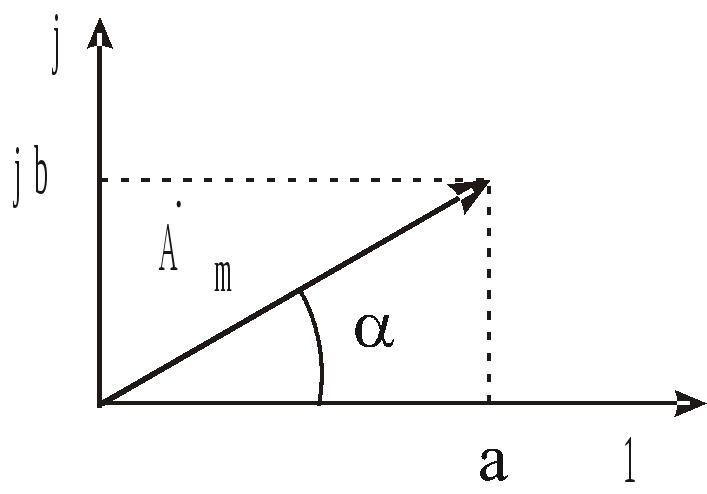
Рис. 3.1

Любое комплексное число может быть представлено в трех формах записи:

а) алгебраическая форма

, (3.1)

где – действительная часть комплексного числа (проекция вектора на действительную ось);

– мнимая часть комплексного числа (проекция вектора на мнимую ось);

б) показательная форма

, (3.2)

где – модуль (длина вектора) комплексного числа ;

– аргумент комплексного числа (угол между действительной осью и вектором );

в) тригонометрическая форма

. (3.3)

Отметим, что все три формы записи однозначно определяют положение вектора на комплексной плоскости.

Изобразим вектор длиной (рис. 3.2), вращающийся на комплексной плоскости с угловой скоростью в положительном направлении (против часовой стрелки).

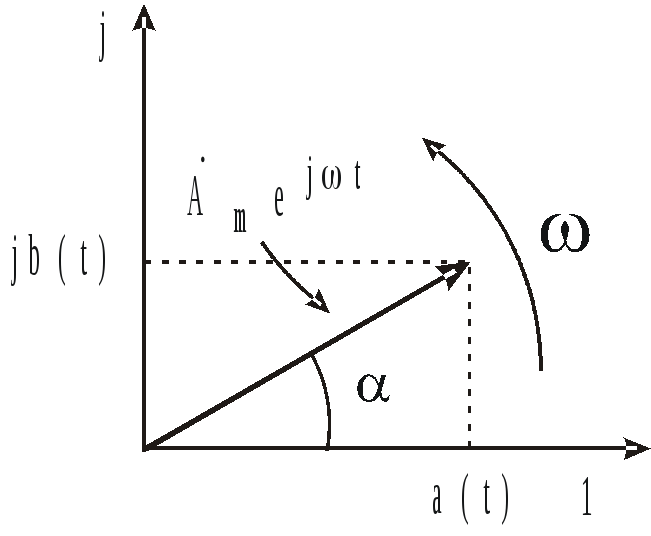
Рис. 3.2

Пусть начальное положение вектора (при t = 0) – под углом к действительной оси. Очевидно, что проекции вращающегося вектора на действительную и мнимую оси являются функциями времени:

. (3.4)

Отметим, что входящий в формулу (3.4) сомножитель является неподвижным вектором на комплексной плоскости (см. рис. 3.1), а его произведение на дает вращающийся вектор. Поэтому сомножитель называется оператором вращения. Умножение любого неподвижного вектора на оператор вращения означает поворот исходного вектора на угол в положительном направлении.

В соответствии с (3.4) мнимая часть комплексной функции есть синусоидальная функция времени . Поэтому синусоидальный ток

(3.5)

может рассматриваться как проекция вращающегося вектора на мнимую ось (рис. 3.3).

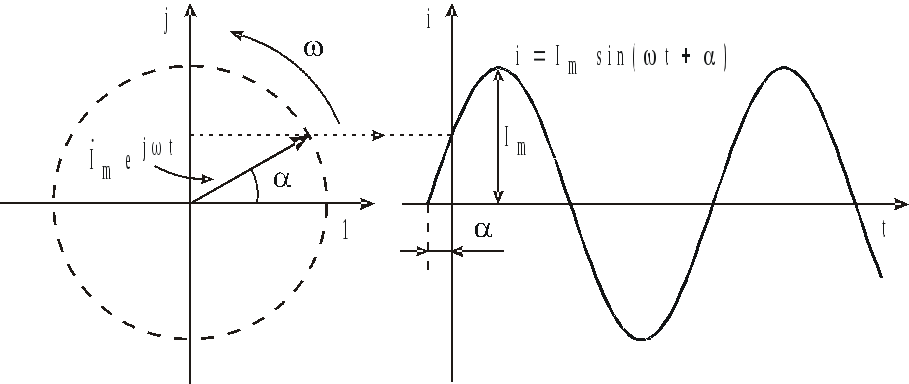
Рис. 3.3

Назовем комплексной амплитудой тока величину

. (3.6)

Если разделить левую и правую части (3.5) на , то получим комплексное действующее значение тока

. (3.7)

3.1. Законы Ома и Кирхгофа в комплексной форме записи

с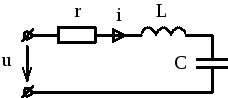

Рис. 3.4

Пусть к цепи рис. 3.4 приложено синусоидальное напряжение

. (3.8)

Требуется определить ток, который будем отыскивать в виде

. (3.9)

Здесь

, – неизвестные пока амплитуда и начальная фаза тока.

Согласно второму закону Кирхгофа

. (3.10)

Отметим, что выражение (3.10) представляет собой интегро-дифферен­ци­аль­ное уравнение, составленное относительно мгновенных значений напряжения и тока.

Перепишем (3.10) с учетом (3.5):

. (3.11)

Здесь комплексные амплитуды напряжения и тока могут быть представлены в показательной форме записи: , .

Операции дифференцирования и интегрирования мнимой части комплексной функции и операция взятия самой мнимой части взаимно переместимы, поэтому перепишем (3.11) в виде

. (3.12)

Полученное уравнение справедливо для любого момента времени, поэтому выражения в квадратных скобках правой и левой частей равны:

. (3.13)

Осуществляя дифференцирование и интегрирование в (3.13), получим

. (3.14)

Разделим левую и правую части (3.14) на оператор вращения :

. (3.15)

Для анализа полученного выражения (3.15) введем обозначения:

а) комплексное сопротивление сопротивления

; (3.16)

б) комплексное сопротивление индуктивности

; (3.17)

в) комплексное сопротивление емкости

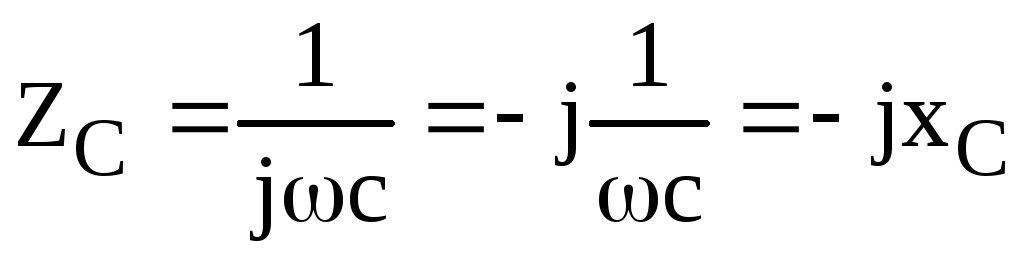; (3.18)

г) комплексная амплитуда напряжения на сопротивлении

; (3.19)

д) комплексная амплитуда напряжения на индуктивности

; (3.20)

е) комплексная амплитуда напряжения на емкости

. (3.21)

Формулы (3.19)–(3.21) представляют собой закон Ома в комплексной форме записи для отдельных пассивных элементов цепи.

Перепишем (3.15) с учетом принятых обозначений:

. (3.22)

Очевидно, что формулы (3.15) и (3.22) представляют собой второй закон Кирхгофа в комплексной форме записи для рассматриваемой цепи (рис. 3.4) Таким образом, использование комплексного метода позволило осуществить переход от интегро-дифференциального уравнения (3.10) к алгебраическому уравнению (3.15), составленному относительно комплексов тока и напряжения.

Для определения комплексной амплитуды искомого тока перепишем (3.15) в виде

. (3.23)

Обозначим входное комплексное сопротивление цепи как

. (3.24)

Перепишем (3.24) в показательной форме записи:

. (3.25)

Тогда

. (3.26)

После определения комплексной амплитуды тока переходим к его мгновенному значению .

Составим в качестве примера уравнения по законам Кирхгофа для цепи рис. 3.5.

с

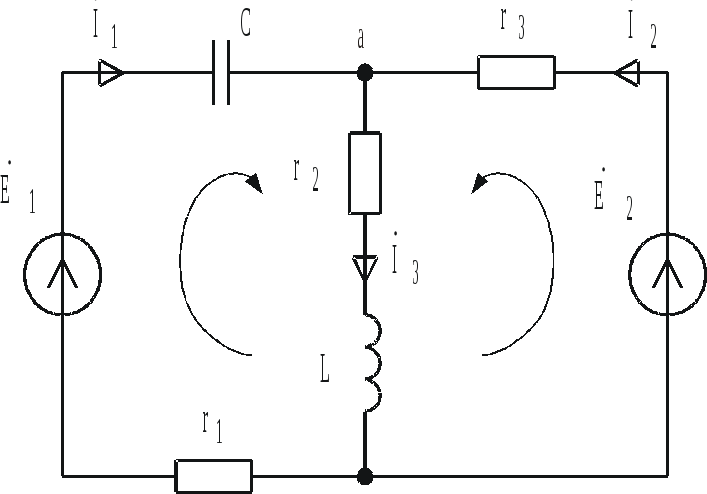
Рис. 3.5

Отметим, что в качестве обозначений в схеме рис. 3.5 использованы комплексные действующие значения ЭДС и токов. Направления последних выбраны произвольно.

Первый закон Кирхгофа для узла а:

.

Для составления уравнений по второму закону Кирхгофа произвольно выбираем независимые контуры и направления их обхода (см. рис. 3.5). Сами уравнения имеют вид

,

.