8.3 Кинематика теории относительности (следствия из преобразований Лоренца)

1. Нарушение одновременности удаленных событий. Пусть в системе (условно неподвижной) в точках с координатами x₁ и x₂ происходят одновременно два события в момент времени t₁ = t₂ = t₀. Тогда для наблюдателя, находящегося в системе , движущейся со скоростью относительно системы , время наступления этих событий будет разным:

; .

То есть из этих соотношений видно, что .

Следовательно, для удаленных точек одновременность нарушается.

Однако если x₁ = x₂, то и , т.е. события, происходящие одновременно в одном и том же месте в системе , будут совпадать в пространстве и времени и в системе .

2. Длительность событий в разных системах. Предположим, что в системе K в точке, координата которой x не изменяется, происходит некоторое событие, длительность которого

,

где t₁ и t₂ – моменты начала и окончания события соответственно.

Длительность этого события для наблюдателя, находящегося в системе ,

;

.

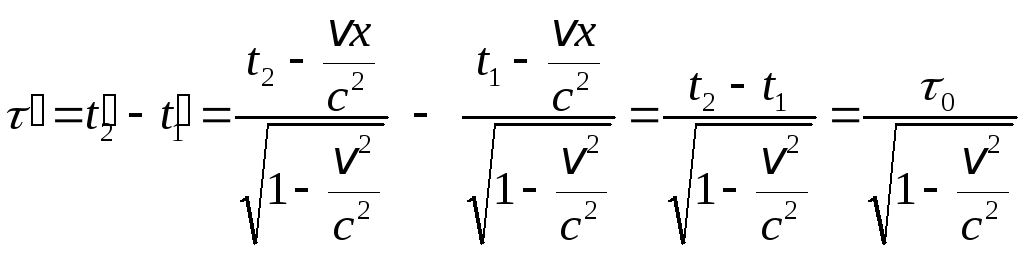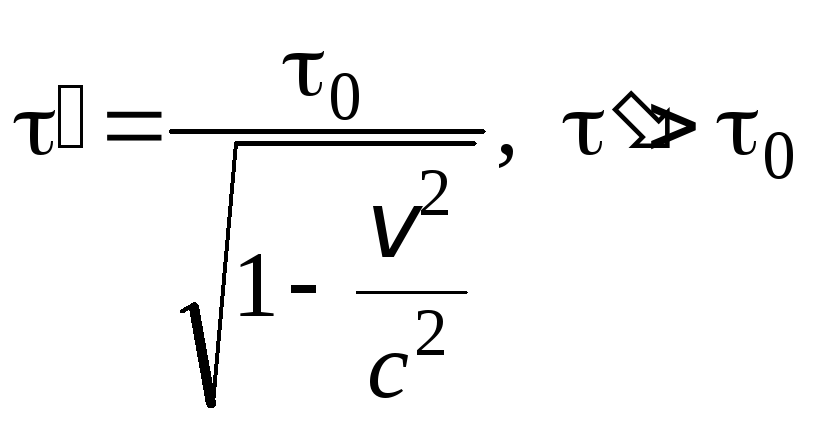Отсюда видно, что длительность события, происходящего в некоторой точке пространства, минимальна в той инерциальной системе отсчета, относительно которой эта точка неподвижна.

Длительность события , отсчитанная по часам, находящимся в той системе, относительно которой точка неподвижна называют собственным временем. Как видно из полученной формулы , и собственное время события всегда меньше, чем время, отсчитанное по часам в движущейся системе отсчета.

Этот релятивистский эффект замедления времени получил непосредственное подтверждение в опытах с m-мезонами, элементарными частицами, входящими в состав космических лучей. Среднее время жизни неподвижного m-мезона равно . Мезоны возникают в атмосфере на высоте 20-30 км и в значительном количестве достигают поверхности Земли. Но исходя из представлений классической механики и времени жизни с мезон, даже двигаясь со скоростью света, мог бы пролететь всего м. Чем же объяснить, что они достигают поверхности Земли? Время жизни неподвижного мезона с. Если он двигается, то в системе отсчета, движущейся вместе с ним, он будет оставаться неподвижным и время его жизни будет тем же самым, т.е. с– это собственное время жизни мезона. Время же по часам экспериментатора, связанного с Землей, оказывается гораздо больше: . Так как скорость мезонов близка к скорости света, то и за это время они успевают достигнуть поверхности Земли.

3. Длина тел в разных системах отсчета . Предположим, что некоторый стержень, находящийся в условно неподвижной системе K, расположен вдоль оси x и имеет в этой системе длину

.

Длина этого стержня в системе , движущейся относительно стержня со скоростью в направлении оси x,

Координаты надо измерять в один и тот же момент времени , определяемый в системе . Для этого выразим x через по преобразованиям Лоренца:

; .

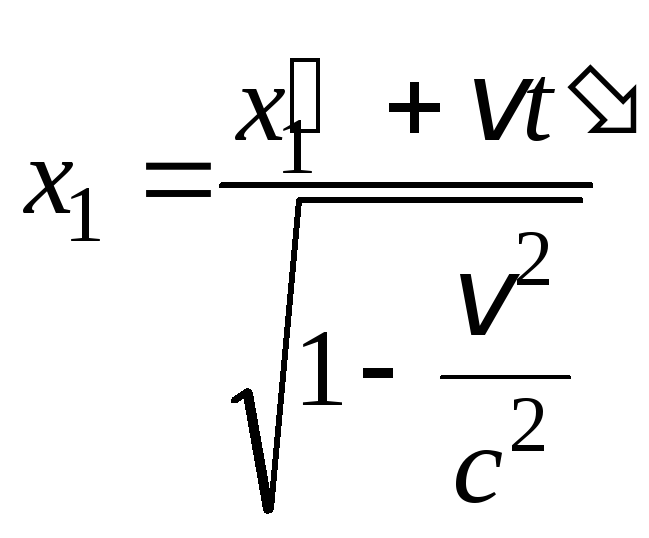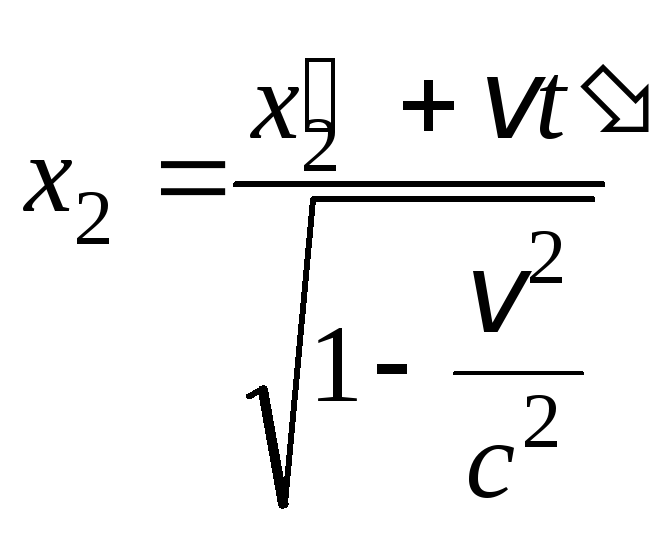Вычитая левые и правые части равенств, получим

но и , поэтому

.

Стержень в координатной системе, движущейся относительно его, короче, чем в системе, где стержень покоится ().

4. Закон сложения скоростей.

В классической механике закон сложения скоростей, получающийся из преобразований Галилея, записывается так:

,

где – скорость некоторого тела относительно условно неподвижной системы отсчета ; –скорость этого же тела в условно движущейся системе отсчета ; – переносная скорость движения системы относительно системы .

Из преобразований Лоренца следует иная связь между перечисленными скоростями:

.

Покажем, что при малых по сравнению со скоростью света скоростях, т.е. если и формула сложения скоростей теории относительности переходит в классическую формулу. Действительно, выражением стоящем в знаменателе, можно пренебречь по сравнению с единицей и в результате получаем классическую формулу сложения скоростей.

Теперь рассмотрим пример, когда .

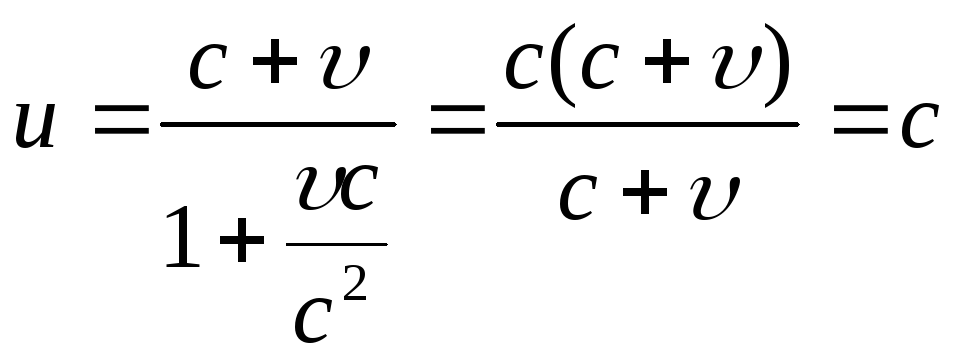
Рассмотрим, наконец, пример, когда и .

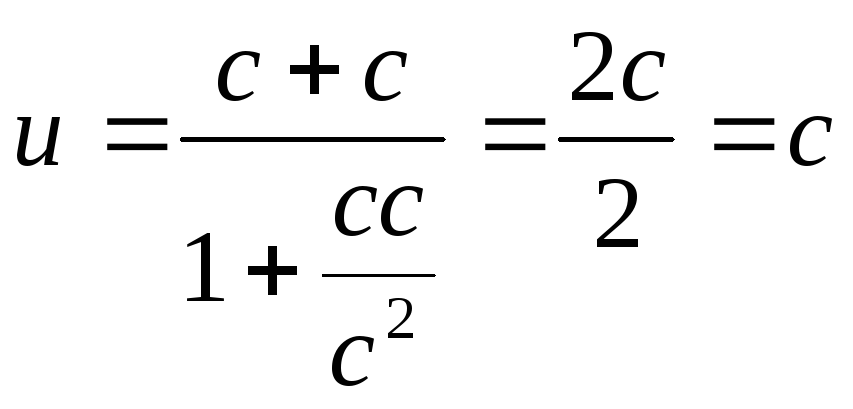
То есть и в этом случае скорость u=c.

Из этих примеров виден предельный характер скорости света, а также то, что скорость света одинакова во всех системах отсчета. Таким образом, постоянство скорости света непосредственно вытекает из преобразований Лоренца.