3.6. Условия равновесия твердых тел

Движение твердого тела определяется двумя уравнениями:

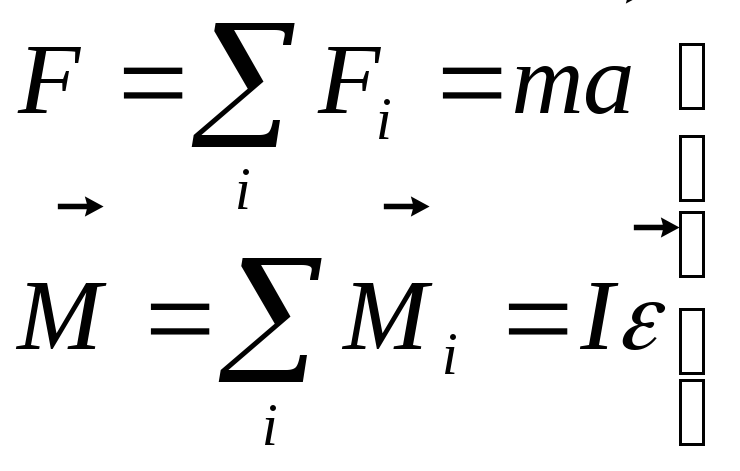, (22)

где – внешние силы; – моменты этих сил, - ускорение центра масс тела, - угловое ускорение. Тело может оставаться в состоянии покоя в том случае, если нет причин, приводящих к возникновению поступательного движения или вращения. В соответствии с (22) для этого необходимо и достаточно, чтобы были выполнены два условия:

1. Сумма всех внешних сил, приложенных к телу, должна быть равна нулю:

.

2. Результирующий момент всех внешних сил относительно любой неподвижной оси должен быть равен нулю:

.

3.7. Работа внешних сил при вращении твердого тела

Рассмотрим твердое тело, которое может вращаться вокруг неподвижной в пространстве оси вращения.

Допустим, что F_i – составляющая внешней силы вызывающая вращение и приложенная к некоторой элементарной массе ∆m_i твердого тела. За малый промежуток времени элементарная масса переместится на и следовательно силой будет совершена работа

,

где – сила касательная к траектории движения массы (именно эта сила вызывает вращение тела), величина перемещения , где - элементарный угол поворота твердого тела.

Следовательно

Легко заметить, что произведение является моментом силы относительно заданной оси вращения z и действующим на элемент тела Dm_i. Следовательно, работа силы будет равна

.

Суммируя работу моментов сил, приложенных ко всем элементам тела, получим для элементарно малой энергии, затрачиваемой на элементарный поворот тела dj:

,

где – проекция на ось z результирующего момента сил, действующих на твердое тело, вращающееся вокруг заданной оси. Заметим, что (где - угловая скорость вращения тела).

И окончательно для работы за конечный промежуток времени t имеем:

.

И, наконец, отметим, что имеется формальная аналогия величин для поступательного и вращательного движений, представленная в таблице:

Поступательное движение	Вращательное движение
– сила т – масса – линейное ускорение – импульс тела – работа силы	– момент силы – момент инерции – угловое ускорение – момент импульса – работа момента силы

3.8. Неинерциальные системы отсчета

Классические законы механики Ньютона справедливы только в инерциальных системах отсчета. Однако встречаются задачи, для которых движение тел задается в системах, жестко связанных с телами, на которые действуют силы, т.е. в неинерциальных системах отсчета. Рассмотрим вначале конкретный пример. Допустим автобус, подходя к остановке, тормозит. Пассажиры автобуса при этом увлекаются по направлению к кабине шофера, хотя их никто не толкает (нет внешней силы, действующей на пассажиров). Таким образом, для того чтобы правильно рассчитывать движение пассажиров по отношению к стенкам автобуса (неинерциальная система отсчета), необходимо во второй закон Ньютона ввести добавочное слагаемое, т.е. добавочную силу, которая будет учитывать ускоренное движение пассажиров по отношению к стенкам автобуса. Это слагаемое называют силой инерции:

,

где – сила инерции; – ускорение системы отсчета (автобуса).

Второй закон Ньютона в ускоренно движущейся системе отсчета тогда будет:

или в развернутом виде

,

где – сила, действующая на тело со стороны других тел; – ускорение тела в неинерциальной системе отсчета; – ускорение системы отсчета. Силу инерции необходимо учитывать, только в том случае, если расчеты производятся в системе отсчета движущейся ускоренно.

Рассмотрим теперь вращающуюся систему отсчета. Допустим, что некоторое тело в этой системе отсчета неподвижно, т.е. вращается вместе с системой отсчета, двигаясь по круговой траектории. Так как тело неподвижно в неинерциальной системе отсчета, то необходимо считать, что сумма всех сил, действующих на это тело в этой системе, равна нулю. Но это означает, что во вращающейся системе отсчета необходимо ввести силу, которая скомпенсирует центростремительную силу. Эту силу называют центробежной. Численно центробежная сила равна центростремительной и направлена в противоположную сторону. Формула для центробежной силы

,

где w – угловая скорость вращения системы отсчета; – радиус вектор, проведенный от оси вращения в точку расположения тела. Подчеркнем еще раз: центробежную силу необходимо учитывать, только в том случае, если расчеты производятся во вращающейся системе отсчета.

Допустим теперь, что тело движется во вращающейся системе отсчета с некоторой постоянной скоростью . Тогда, кроме центробежной силы, необходимо учитывать так называемую силу Кориолиса. Сила Кориолиса равна:

,

где – векторное произведение скорости тела во вращающейся системе координат и угловой скорости вращения этой системы.

Таким образом, в общем случае, когда система отсчета движется ускоренно и кроме этого вращается, а также изучаемое тело в этой системе движется со скоростью , уравнение движения необходимо записать в следующем виде:

или более подробно:

,

где – сила, действующая на изучаемое тело со стороны других тел; – ускорение системы отсчета; – угловая скорость вращения системы отсчета; – скорость тела в неинерциальной системе отсчета; – ускорение тела, измеренное в неинерциальной системе отсчета.