3.5. Основное уравнение динамики вращательного движения твердого тела

O

m_i

O

Рис.16

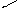
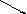
Рассмотрим твердое тело, которое может вращаться вокруг неподвижной в пространстве оси вращения ОО (рис.16). Разобьем все тело на элементарные массы m_i. В общем случае к каждой элементарной массе может быть приложена некоторая внешняя сила . Составляющая силы , вызывающая вращение должна быть направлена по касательной к окружности, по которой движется элементарная масса. Остальные две составляющие внешней силы вызывают либо деформацию фиксированной в пространстве оси вращения, либо определяют нагрузку на опоры оси вращения, но вращения не вызывают. Обозначим равнодействующую всех внешних сил приложенных к некоторой элементарной массе m_i и вызывающих вращение через (рис.16). Внутренние силы, действующие между элементарными массами твердого тела, учитывать не будем, так как при последующем суммировании, как сами силы, так и их моменты взаимно сокращаются (III закон Ньютона!).

По второму закону Ньютона, имеем:

, (18)

где , – линейное ускорение и радиус-вектор элементарной массы;  – угловое ускорение вращения тела, как единого целого ().

Умножим обе части (18) на r_i:

.

Так как F_ir_i = М_i по определению является моментом силы, действующим на элемент массы m_i относительно заданной оси вращения, то следовательно:

.

Суммируя по всем элементарным массам, на которое разбито тело, получим:

.

Величина суммы – это момент инерции тела относительно заданной оси вращения, поэтому последнее выражение можно записать в следующей форме:

, (19)

где – проекция на заданную ось вращения суммарного момента внешних сил, действующих на твердое тело;  – величина углового ускорения.

Напомним, что момент сил относительно заданной оси вращения, является проекцией вектора момента сил на ось вращения. Поэтому, в общем случае, когда ось вращения не фиксирована в пространстве, вращение вызывается не одной проекцией момента сил, а всеми тремя проекциями, т.е. вектором момента сил . Поэтому, уравнение (19) можно записать в следующей форме:

. (20)

Добавочно напомним, что момент инерции твердого тела I в общем случае зависит от пространственного положения оси вращения.

Уравнение (20) является основным уравнением динамики вращательного движения. По форме оно сходно с уравнением II закона Ньютона и его иногда называют вторым законом динамики для вращательного движения.

Основное уравнение вращательного движения может быть дано и в иной математической редакции. Для этого вспомним, что угловое ускорение определяется производной от угловой скорости по времени: . После подстановки в (20) имеем: . Если I-const, то внося величину I под знак производной, получим:

.

Выражение, стоящее в скобках является моментом импульса твердого тела и поэтому основной закон динамики вращательного движения твердого тела можно записать еще в одной математической редакции:

. (21)