
- •Содержание
- •Классическое и геометрическое определение вероятности Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Комбинаторика. Бином Ньютона Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Полная вероятность Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Формула Байеса Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Непрерывные случайные величины Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Статистические методы обработки данных Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Оценка параметров генеральной совокупности Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Ключи к тестовым заданиям
Тестовые задания для самостоятельного решения
-
Легкое. Пусть (3, 0, 4, 3, 6, 0, 3, 1) - наблюдавшиеся значения выборки. Значение эмпирической функции распределения F(3) равно ...
а) 2/8
б) 3/8
в) 5/8
г) 2
д) 5
-
Средней трудности. Эмпирическая функция распределения, построенная по 100 наблюдениям, имеет вид

Тогда мода выборочного распределения равна…
а) 2,8
б) 2
в) 1,1
г) 4
д) 1
-
Трудное. По результатам распределения 100 рабочих по тарифным разрядам найдена эмпирическая функция распределения:
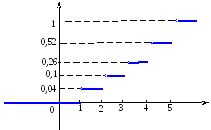
Количество рабочих, имеющих пятый тарифный разряд, равно…
а) 54
б) 48
в) 52
г) 4
д) 46
-
Повышенной трудности. Произведена выборка 100 роликов. По данным отклонений x от номинального размера их диаметров построена гистограмма частот.
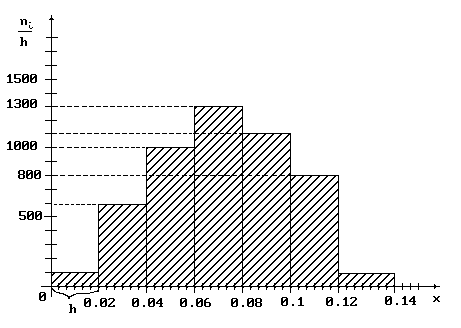
Тогда число роликов, удовлетворяющее
неравенству
![]() ,
равно…
,
равно…
а) 74
б) 34
в) 26
г) 68
д) 46
-
Легкое. Пусть X1, X2, …, Xn – выборка из распределения Пуассона с неизвестным параметром . Какая из перечисленных ниже функций НЕ ЯВЛЯЕТСЯ статистикой?
а)
![]()
б)
![]()
в)
![]()
г)
![]()
д)
![]()
-
Оценка параметров генеральной совокупности Основные определения
-
Несмещенная оценка
 для параметра
для параметра
 – оценка обладающая свойством
– оценка обладающая свойством
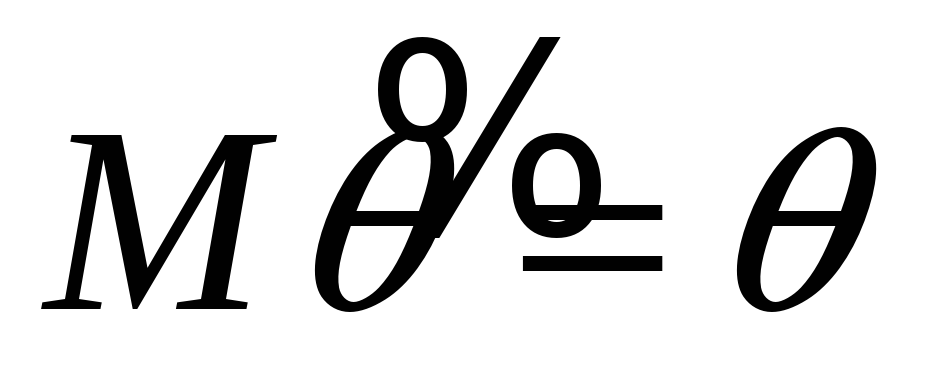 .
. -
Состоятельная оценка
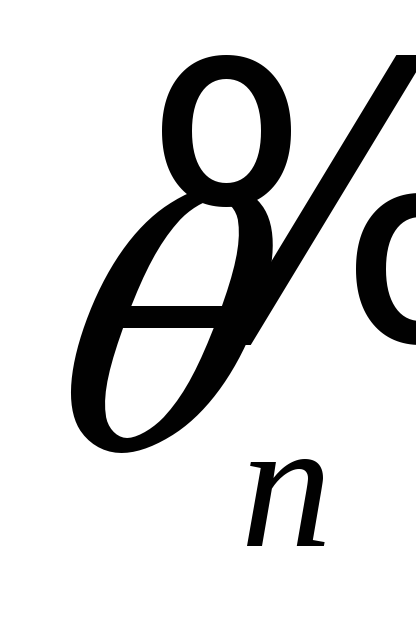 для параметра
для параметра
 – оценка обладающая свойством
– оценка обладающая свойством
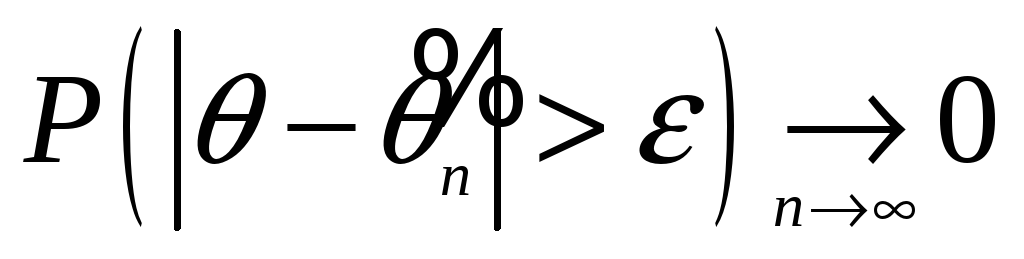 .
. -
Эффективная оценка – оценка обладающая наименьшей дисперсией среди всех возможных оценок параметра
 .
. -
Несмещенная и состоятельная оценка математического ожидания: выборочное среднее
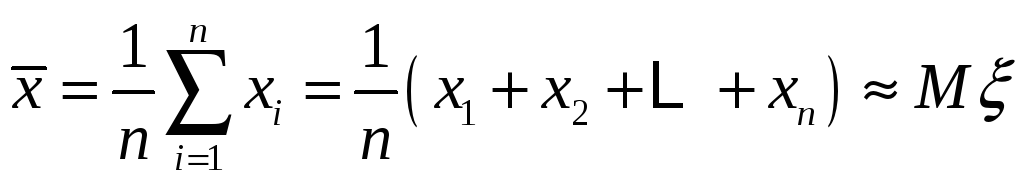 .
Если ξ распределена нормально, то
.
Если ξ распределена нормально, то
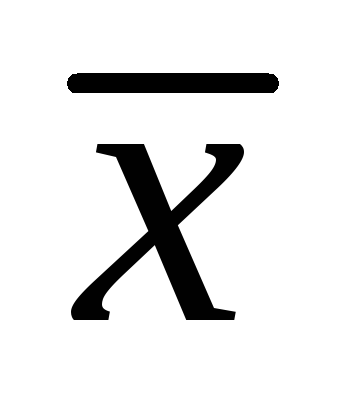 является также эффективной оценкой.
является также эффективной оценкой. -
Несмещенная и состоятельная оценка дисперсии: исправленная выборочная дисперсия
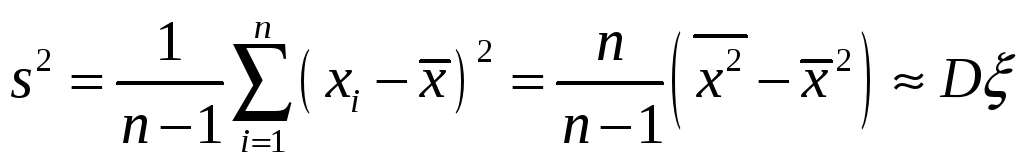 .
. -
Метод моментов – это способ оценивания параметров распределений, при котором теоретические моменты приравниваются к эмпирическим. Например:
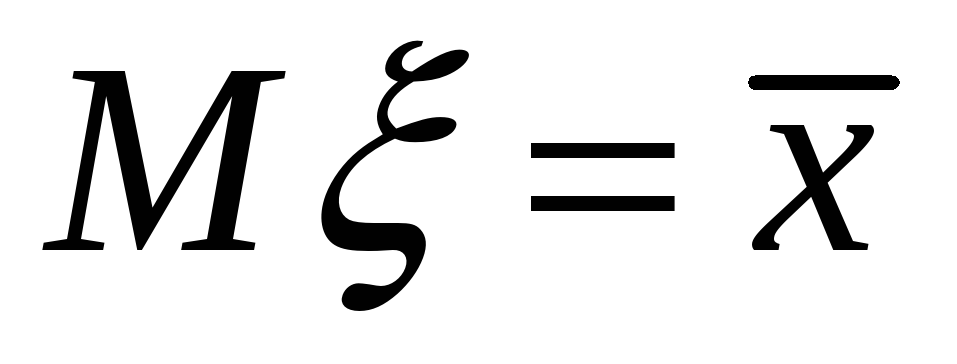 или
или
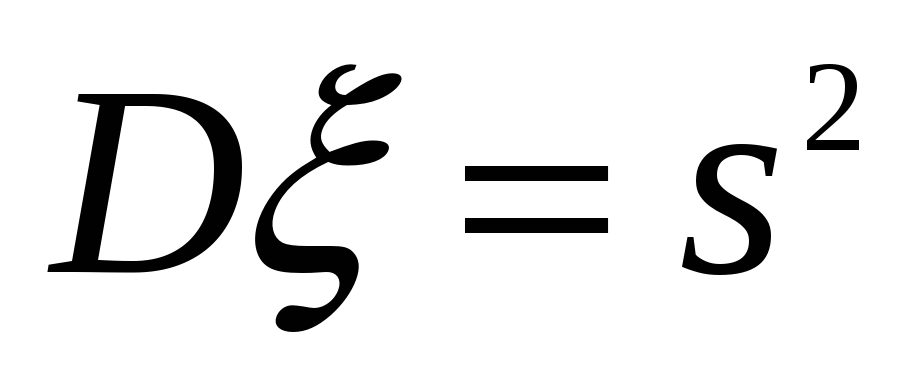 .
.
Примеры решения тестовых заданий
-
После 5 заездов автомобиля были получены значения его скорости (в м/сек): 23; 53; 73; 83; 14. Оценка математического ожидания скорости автомобиля равна…
-
Наилучшей из оценок математического ожидания (при условии, что тип распределения не известен) является величина
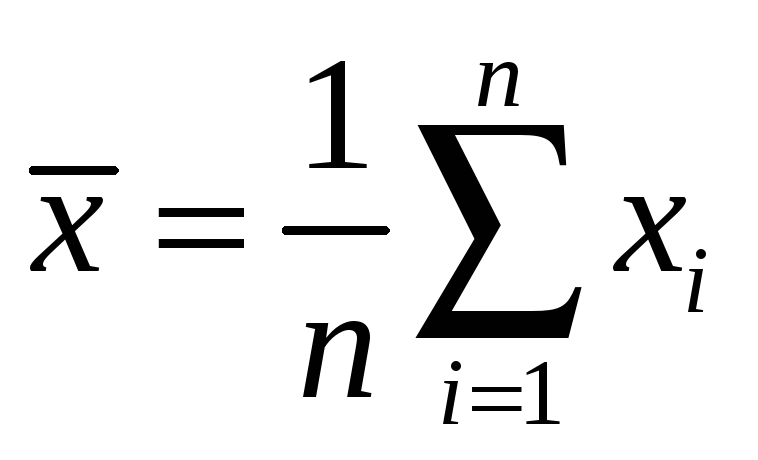 (Определение 8.4.). Вычислим ее значение:
(Определение 8.4.). Вычислим ее значение:
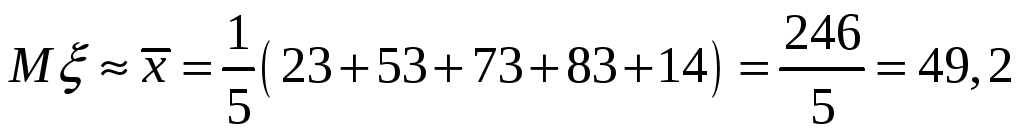 .
.
-
Случайная величина распределена по закону Пуассона. По результатам наблюдаемых значений 3; 4; 6; 4; 2; 3; 3; 4; 4; 1 оценка параметра этого распределения, равна...
-
Так как
 в случае распределения Пуассона,
воспользуемся методом моментов (Определение 8.6.)
для оценки параметра
в случае распределения Пуассона,
воспользуемся методом моментов (Определение 8.6.)
для оценки параметра
 .
Оценкой для
.
Оценкой для
 является величина
является величина
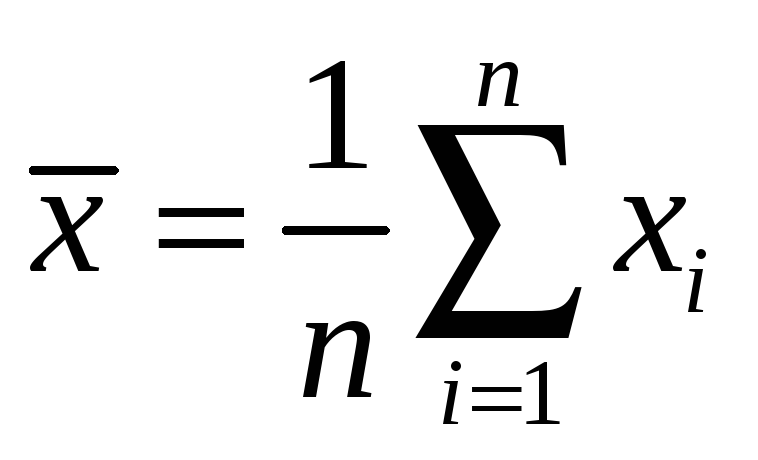 .
Вычислим ее значение:
.
Вычислим ее значение:
![]() .
.
-
Случайная величина распределена равномерно на интервале [a, 8], где a – неизвестный параметр. По результатам наблюдений значений величины 8, 5, 7, 6, 5, 5, 6 несмещенная оценка параметра a равна…
-
В случае равномерного распределения
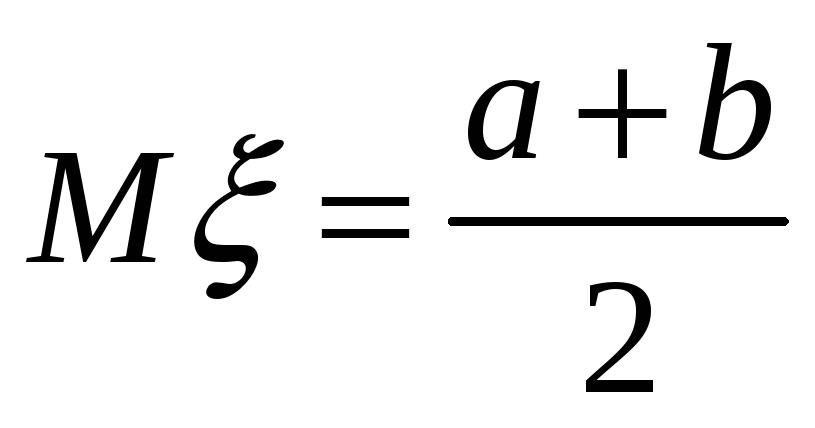 (Определение 6.5.). Оценим параметр a,
воспользовавшись методом моментов
(Определение 8.6.).
(Определение 6.5.). Оценим параметр a,
воспользовавшись методом моментов
(Определение 8.6.).
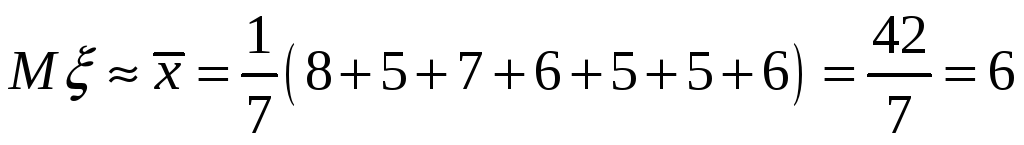 .
Отсюда
.
Отсюда
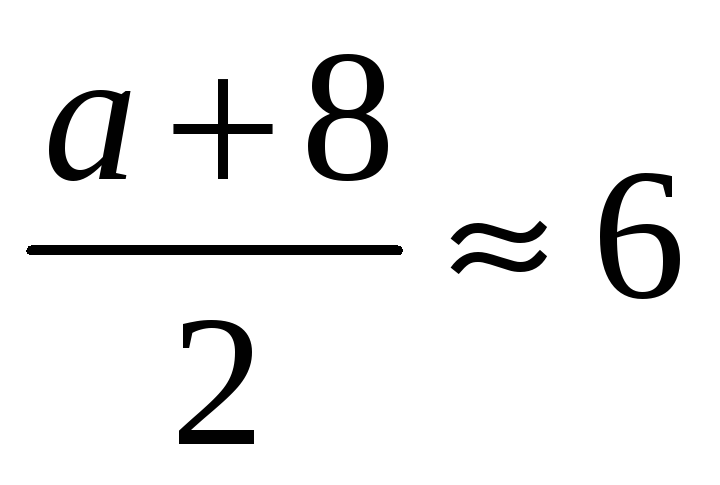 и
и
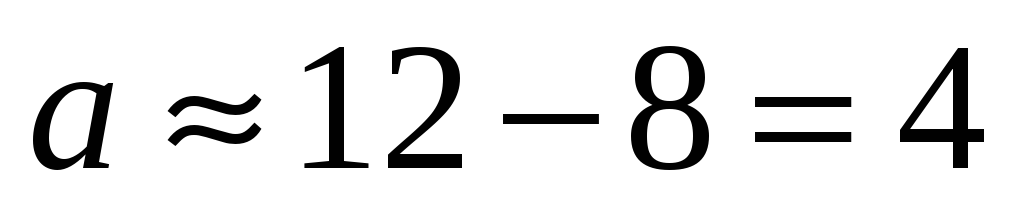 .
.
-
При контрольных измерениях количество одноногих кур на 1000 особей составило 0, 1, 0, 2, 0, 1, 1, 1. Тогда оценка количества окороков при забое 20 000 кур составляет…
-
Количество одноногих кур
 подчиняется биномиальному распределению.
Математическое ожидание биномиального
распределения (Определение 5.4.)
подчиняется биномиальному распределению.
Математическое ожидание биномиального
распределения (Определение 5.4.)
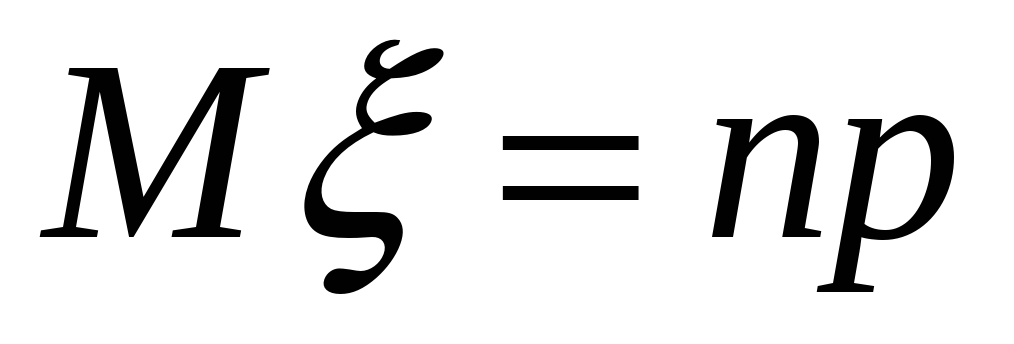 .
Оценим параметр p,
воспользовавшись методом моментов.
.
Оценим параметр p,
воспользовавшись методом моментов.
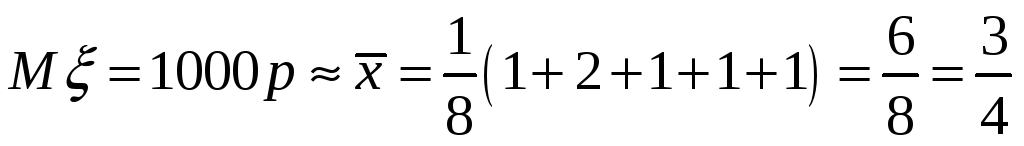 .
Отсюда
.
Отсюда
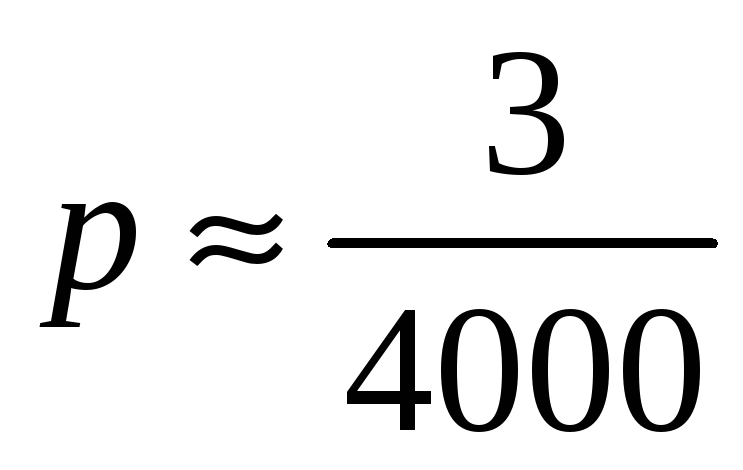 .
Поскольку параметр p
постоянный в каждом опыте, оценим
количество одноногих кур при забое 20
000 штук.
.
Поскольку параметр p
постоянный в каждом опыте, оценим
количество одноногих кур при забое 20
000 штук.
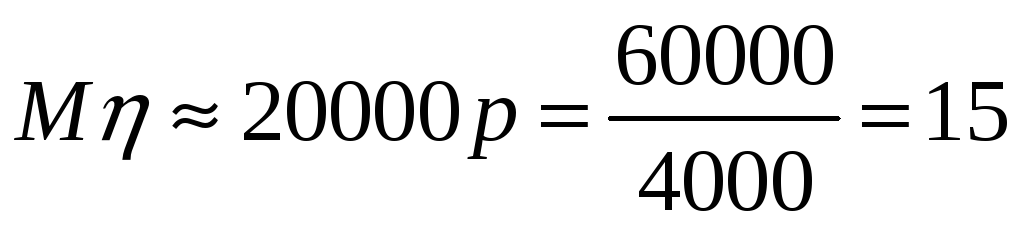 .
Таким образом, оценка количества
окороков составит:
.
Таким образом, оценка количества
окороков составит:
 .
.
