
- •Содержание
- •Классическое и геометрическое определение вероятности Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Комбинаторика. Бином Ньютона Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Полная вероятность Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Формула Байеса Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Непрерывные случайные величины Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Статистические методы обработки данных Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Оценка параметров генеральной совокупности Основные определения
- •Примеры решения тестовых заданий
- •Тестовые задания для самостоятельного решения
- •Ключи к тестовым заданиям
Примеры решения тестовых заданий
-
Игральная кость бросается один раз. Вероятность того, что появится НЕ МЕНЕЕ 4 очков, равна…
-
В классической схеме определения вероятностей (Определение 1.10.) сначала следует определить пространство элементарных исходов эксперимента . В данном случае элементарный исход – это выпавшее количество очков, поэтому = {1, 2, 3, 4, 5, 6}. Следующее действие состоит в том, чтобы подсчитать количество элементарных исходов, при реализации которых наступает интересующее нас событие. Событие А = {выпало НЕ МЕНЕЕ 4 очков} наступает тогда, когда на игральной кости выпадет 4, 5 или 6 очков. Всего три элементарных исхода, благоприятствующих событию А. Делим количество благоприятствующих исходов на общее число возможных исходов
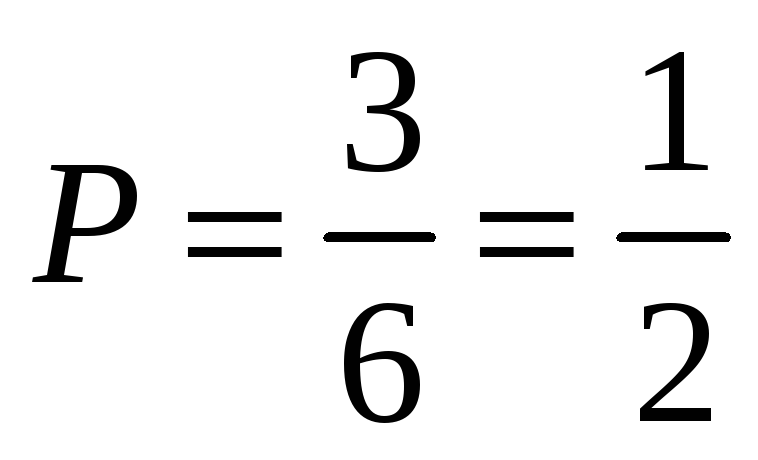 .
.
-
В стопке 12 тетрадей. Из них 7 в клетку, остальные в линию. Из стопки наугад выбирают сразу две тетради. Вероятность того, что они обе в клетку, равна …
-
В таких задачах удобно представлять себе одинаковые объекты разными. Например, тетради в клетку имеют разноцветные обложки или на них написаны инвентарные номера и т.п. Посчитаем количество способов выбора двух тетрадей в клетку. Будем выбирать тетради по очереди. Первая тетрадь в клетку может быть одного из 7 цветов. Значит, есть 7 вариантов выбора первой тетради. После того, как выбрана первая тетрадь, осталось еще 6 в клетку. Из них будем выбирать вторую. Значит, есть 6 вариантов выбора второй тетради. На каждую, выбранную первой тетрадь в клетку, приходится по 6 вариантов выбора второй тетради в клетку. Поэтому общее число вариантов выбора двух тетрадей в клетку из семи, находящихся в стопке, равно
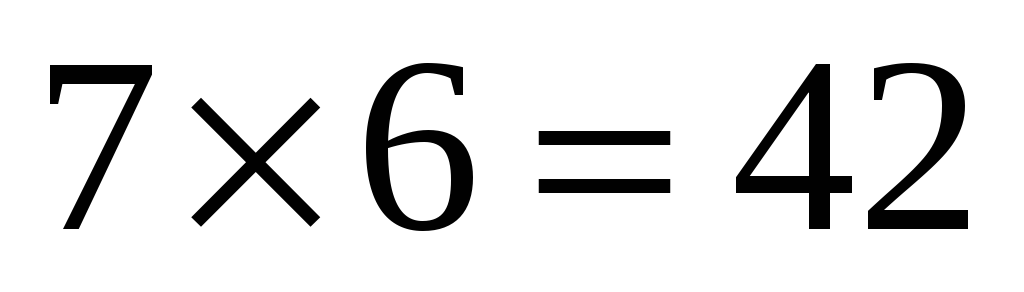 .
Но следует учесть, что при таком способе
подсчета, все возможные варианты будут
посчитаны дважды. Например, если первой
была выбрана тетрадь синего цвета, а
потом красного, то, в следующий раз
может получиться так, что первой окажется
красная тетрадь, а потом синяя. Таким
образом, чтобы получить количество
способов выбора без учета порядка,
следует поделить общее число вариантов
на количество способов упорядочивания,
т.е. в данном случае на 2. Благоприятных
исходов
.
Но следует учесть, что при таком способе
подсчета, все возможные варианты будут
посчитаны дважды. Например, если первой
была выбрана тетрадь синего цвета, а
потом красного, то, в следующий раз
может получиться так, что первой окажется
красная тетрадь, а потом синяя. Таким
образом, чтобы получить количество
способов выбора без учета порядка,
следует поделить общее число вариантов
на количество способов упорядочивания,
т.е. в данном случае на 2. Благоприятных
исходов
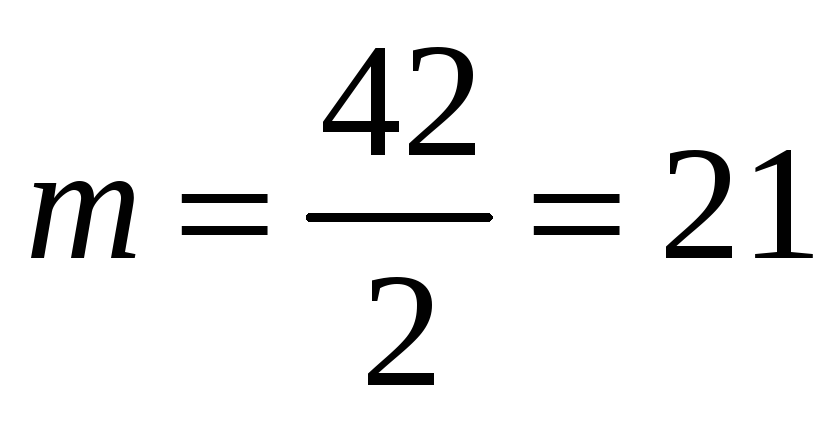 (Определение 1.11.). Действуя по аналогичной
схеме, можем посчитать общее количество
способов выбора двух тетрадей из
имеющихся двенадцати
(Определение 1.11.). Действуя по аналогичной
схеме, можем посчитать общее количество
способов выбора двух тетрадей из
имеющихся двенадцати
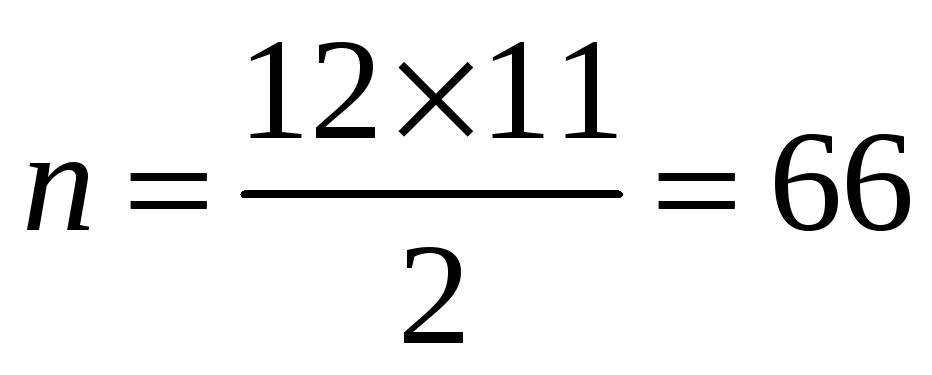 (Определение 1.11.). Искомая вероятность
(Определение 1.10.)
(Определение 1.11.). Искомая вероятность
(Определение 1.10.)
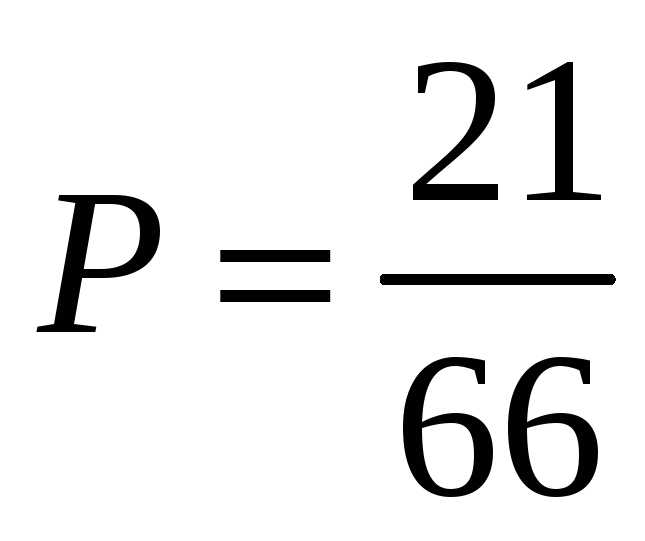 .
.
-
Бросаются три игральные кости один раз. Вероятность того, что сумма очков составит 17, равна…
-
Чтобы в сумме выпало 17, на двух костях из трех должны выпасть шестерки, а на одной пятерка. Раскрасим одинаковые игральные кости в разные цвета. Например, красный, зеленый и синий. Пятерка может выпасть либо на красной, либо на зеленой, либо на синей игральной кости. Получаем три благоприятные комбинации: {К-5, З-6, C – 6}, {К-6, З-5, C–6}, {К-6, З-6, C–5}. Всего же комбинаций
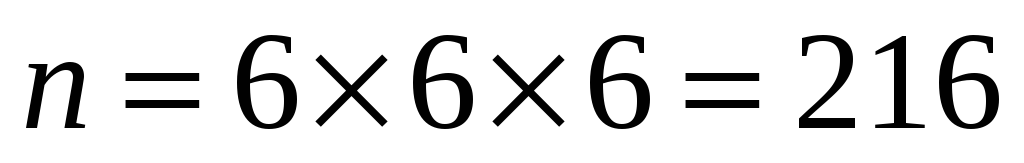 ,
значит, искомая вероятность (Определение 1.10.)
равна
,
значит, искомая вероятность (Определение 1.10.)
равна
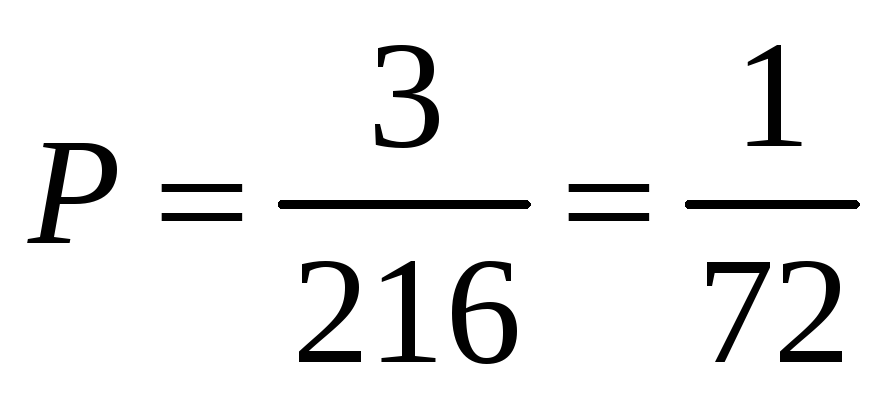 .
.
-
Двое договариваются о встрече в определенном месте, которая должна произойти в промежутке времени от 12 часов до 12 часов и 20 минут. Каждый из договаривающихся приходит к месту встречи в любой наугад взятый момент времени из этого промежутка времени и ждет другого 5 минут (в пределах указанного промежутка времени). Вероятность, что встреча состоится равна ...
-
Это классический пример задачи на геометрическое определение вероятности (Определение 1.12.). Чтобы решить задачу следует сначала определить, а затем геометрически изобразить пространство элементарных исходов. Элементарным исходом в данном эксперименте будет являться пара вида (t1, t2), где числа t1 и t2 заключены в интервале от 12 часов до 12 часов 20 минут. Поскольку начало отсчета нас мало интересует (суть задачи от этого не изменится) можно считать, что t1 и t2 лежат на отрезке [0, 20]. Немаловажным фактором в этой задаче является независимость выбора момента времени двумя игроками, поэтому здесь имеется две степени свободы и геометрически пространство элементарных исходов представляет собой квадрат со стороной 20 (см. рисунок 1). Встреча состоится лишь тогда, когда
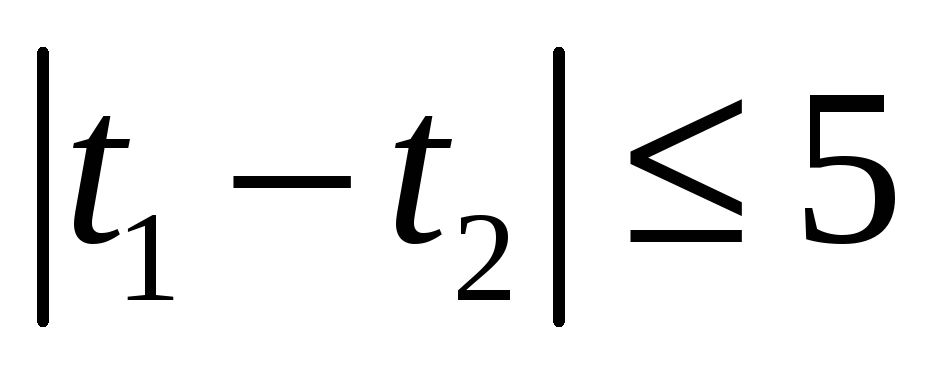 .
Данное условие определяет множество
благоприятствующих встрече исходов.
Геометрически оно представляет собой
полосу шириной 52,
проходящую симметрично вдоль диагонали
квадрата .
.
Данное условие определяет множество
благоприятствующих встрече исходов.
Геометрически оно представляет собой
полосу шириной 52,
проходящую симметрично вдоль диагонали
квадрата .
t1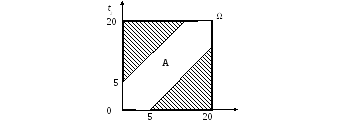
Рис. 1. Геометрическое изображение множества исходов
Отсюда легко определить, что
![]() ,
,
![]() ,
и искомая вероятность
,
и искомая вероятность
![]() .
.
