18. Интерполяционный многочлен Ньютона.
Часто интерполирование
ведется для функций, заданных таблицами
с равноотстоящими значениями аргумента.
В этом случае шаг таблицы
(i=0,1,2,…)
является величиной постоянной. Для
таких таблиц построение интерполяционных
формул заметно упрощается.
Первая интерполяционная формула Ньютона
Пусть для функции,
заданной таблицей с постоянным шагом,
составлена таблица конечных разностей:
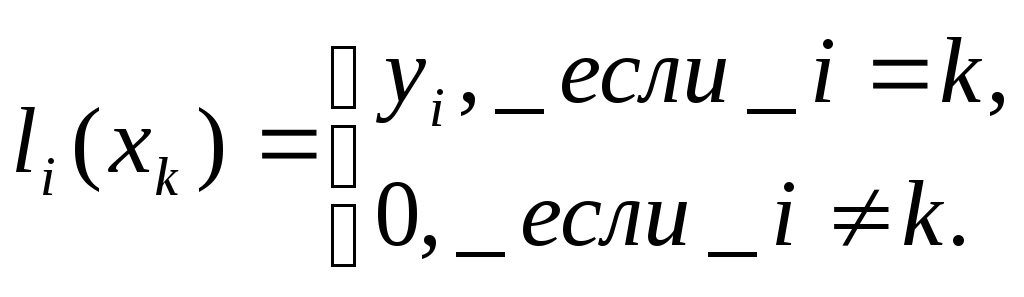Будем искать интерполяционный многочлен
в виде:
(1)
Это многочлен n-й
степени. Значения коэффициентов
найдём из условия совпадения значений
исходной функции и многочлена в узлах.
Полагая
,
из (1) находим
,
откуда
.
Далее, придавая x
значения
и
,
последовательно получаем:
откуда
т. е.
или
откуда
.
Далее, проведя аналогичные выкладки,
можно получить:
;
в общем случае выражение для
будет иметь вид:
.
(2) Подставим
теперь (2) в выражение для многочлена
(1):
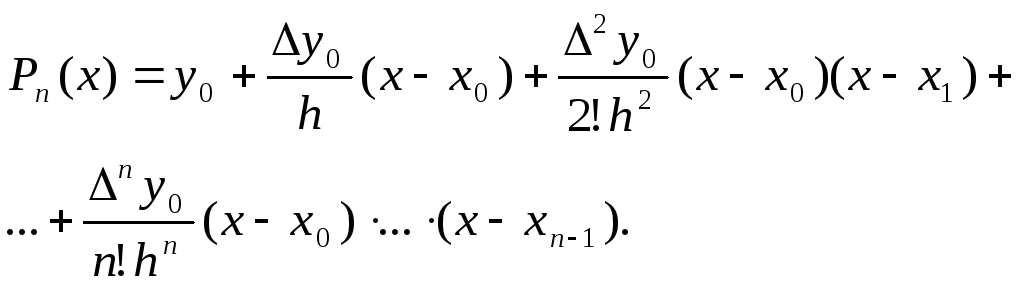(3)
Практически эта формула применяется в
несколько ином виде. Положим
,
т.е.
.
Тогда:
,
и т. д. Окончательно имеем:
.
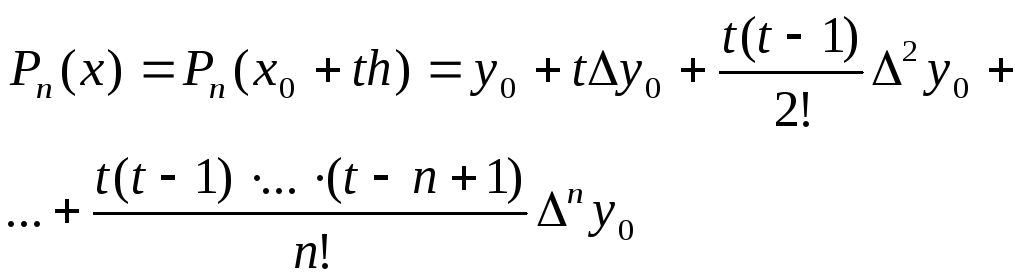(4)
Формула (4) называется первой
интерполяционной формулой Ньютона. Эта
формула применяется для интерполирования
в начале отрезка интерполяции, когда t
мало по абсолютной величине.
Вторая интерполяционная формула Ньютона
Когда значение
аргумента находится ближе к концу
отрезка интерполяции, применять первую
интерполяционную формулу становится
невыгодно. В этом случае применяется
формула для интерполирования назад –
вторая
интерполяционная формула Ньютона,
которая отыскивается в виде:
(5)
Как и для первой формулы Ньютона,
коэффициенты
находятся из условия совпадения значений
функции и интерполяционного многочлена
в узлах:
.
(6)
Подставляя (6) в (5) и переходя к переменной
,
получим окончательный вид второй
интерполяционной формулы Ньютона:
.
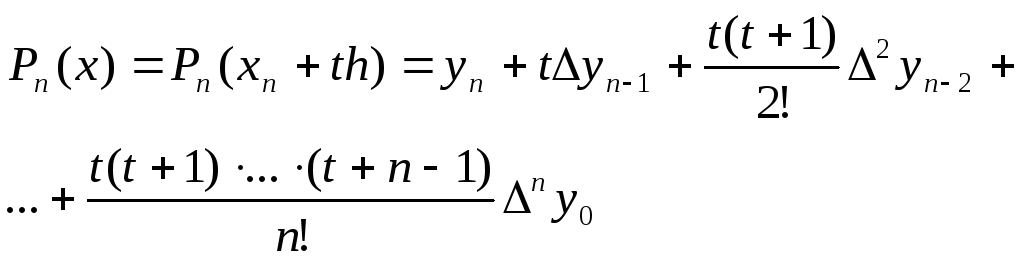(7)
19. Оценки погрешности интерполирования.
Если известно
аналитическое выражение интерполируемой
функции f,
можно применять формулы для оценки
погрешности интерполирования (погрешности
метода). Остаточный член интерполяционного
многочлена
имеет вид:
.
В силу единственности интерполяционного
многочлена для фиксированного отрезка
интерполирования изложение вопроса о
погрешности метода одинаково годится
как для многочлена Лагранжа, так и для
многочлена Ньютона.
Предположим, что
имеет все производные до (n+1)-го
порядка включительно. Введём вспомогательную
функцию
(1)
где k
– постоянный множитель. Как видно,
функция u(x)
имеет n+1
корень (узлы интерполяции
).
Подберём коэффициент k
так, чтобы u(x)
имела (n+2)-й
корень в любой точке
(i=0,1,…n).
Действительно, чтобы было
,
т.е.
достаточно принять
.
(2)
При этом значении k
функция u(x)
будет иметь n+2
корня на отрезке интерполирования и
будет обращаться в нуль на концах каждого
из (n+1)-го
отрезков:
Применяя теорему Роля к каждому из
отрезков, убеждаемся в том, что
имеет не менее (n+1)-го
корня;
имеет не менее n
корней; ………,
имеет не менее одного корня. Пусть
- та самая точка, в которой
.
Продифференцируем (1) n+1
раз:
,
откуда
,
а при
.
(3)
Сравнивая (2) и (3), имеем:
.
Но точка
- произвольная (правда,
от
зависит!), поэтому можно написать:
.
Если принять
,
то
.
(4)
Оценочная формула (4) непосредственно
применима для подсчёта погрешности
метода интерполирования по формуле
Лагранжа. Используя подстановки
и
и заменяя соответствующим образом
выражение для
,
можно получить из (4) формулы оценки
погрешностей интерполирования по
формулам Ньютона:
,(5)
и
,
(6)
Метод Эйлера
Program Eiler; Uses Crt;
Var k:integer; x0,y0,xn,h,y,x:real;
Function f(x,y:real):real;
Begin f:=y; End; Begin ClrScr; Writeln(‘Введите x0:’); Readln(x0);
Writeln('Введите y0:');
Readln(y0);Writeln
('Введите xn:');
Readln(xn);Writeln('Введите k:');Readln(k);h:=(xn-x0)/k;ClrScr;Writeln(' xk ',' yk '); x:=x0;y:=y0;
While x<=xn doBegin Writeln(' ',x:1:2,' ',y:1:5); y:=y+h*f(x,y); x:=x+h; End; Readln; End.
Метод Рунге-Кутта
Program Runge_Kutta;
Uses Crt; Var q,z,q1,q2,
w1,w2,w3,x,y,x0,xn,y0,h,k1,k2,k3,k4,dy:real;
k,i:integer;
Function f(x,y:real):real;
Begin f:=x+y; End;
Begin ClrScr;
Writeln('Введите x0:');
Readln(x0);
Writeln(' Введите y0:');
Readln(y0);
Writeln(' Введите xn:');
Readln(xn);
Writeln(' Введите k:');
Readln(k);h:=(xn-x0)/k;
ClrScr; Writeln(' xk ',' yk ');x:=x0;y:=y0;
Writeln(' ',x:1:2,' ',y:1:6);
For i:=1 to k do Begin
q:=x0; z:=y0; 1:=h*f(x,y);
x:=x+h/2; y:=y+k1/2; k2:=h*f(x,y);
y:=z+k2/2; k3:=h*f(x,y);
x:=q+h; y:=z+k3; k4:=h*f(x,y);
dy:=1/6*(k1+2*k2+2*k3+k4);y:=z+dy; y0:=y; x0:=x;
Writeln(' ',x:1:2,' ',y:1:6);
x:=q+h;End;Readln;End.
Многочлен Лагранжа
Program Lagrange_Interpolation;
Uses Crt; Type mas=array[1..50] of real;
Var N,i,j:integer; A,B,C,
D:mas; i,yi,Z,K,S,x:real;
Begin ClrScr;
Writeln('Введите коли-
чество элементов N:');
Readln(N);
Writeln(' Введите значения xi:');For i:=1 to N do Readln(A[i]);
Writeln(' Введите зна-чения yi:'); For j:=1 to N do Readln(B[j]);ClrScr;
j:=1;Writeln(' xi ',' yi ');
For i:=1 to N do
Begin Write(A[i]:1:3,' ');
Writeln(B[j]:1:3); j:=j+1;
End;Writeln;Z:=1;For i:=1 to N do Begin For j:=1 to N do Begin If i<>j then
Z:=(A[i]-A[j])*Z End;
C[i]:=B[i]/Z;Writeln('A',i,'=',C[i]:6:3); Z:=1;End;
Writeln('Введите произ-вольное значение x:');
Readln(x);K:=1; For i:=1 to N do Begin For j:=1 to N do Begin If i<>j then
K:=(x-A[j])*K End;
D[i]:=C[i]*K; K:=1; End;
S:=0; For i:=1 to N do
S:=S+D[i];Write('Pn(',x:2:3,')=',S:2:3);Readln;End.
Многочлен Ньютона
Program Newton_Interpolation;
Uses Crt; Type mas=array[1..10] of real;
Var i,j,k,m,q,N,s:integer;
Pn,x,hh:real; A,B,C,D,
E:mas;Function Fact(f:integer):integer;
Var i,k:integer; Begin
s:=1; For i:=1 to f do
s:=s*i; Fact:=s; End;
Begin ClrScr; N:=8;
Writeln('Введите значения xi:'); For i:=1
to N do Begin Read(A[i]);
End; Writeln(' Введите значения yi:'); For j:=1
to N do Begin Read(B[j]);
End; ClrScr; j:=1;
Writeln(' xi ',' yi '); For i:=1 to N do Begin
Write(A[i]:2:3,' ');
Writeln(B[j]:2:3); j:=j+1;
End;E[1]:=B[1]; j:=1;
q:=1; For k:=N-1 downto 1 do Begin For i:=1 to N-1 do Begin C[i]:=B[j+1]-B[j]; j:=j+1; End; D[q]:=C[1];
Writeln('D',q,'=',D[q]:2:3);
For m:=1 to N-1 do
B[m]:=C[m];j:=1;q:=q+1;
End;ClrScr;hh:=A[2]-A[1];
Writeln(' Введите значения x:'); Readln(x);
Pn:=E[1]+D[1]*(x-A[1])/(Fact(1)*hh)+D[2]*(x-A[1])*(x-A[2])/(Fact(2)*
exp(2*ln(hh)))+D[3]*(x-A[1])*(x-A[2])*(x-A[3])/(Fact(3)*exp(3*ln(hh)))+D[4]*(x-A[1])*(x-A[2])*(x-A[3])*(x-A[4])/(Fact(4)*exp(4*ln(hh)))+D[5]*(x-A[1])*(x-A[2])*(x-A[3])*(x-A[4])*(x-A[5])/(Fact(5)*
exp(5*ln(hh)))+D[6]*(x-A[1])*(x-A[2])*(x-A[3])*(x-A[4])*(x-A[5])*
(x-A[6])/(Fact(6)*exp(6*ln(hh)))+D[7]*(x-A[1])*(x-A[2])*(x-A[3])*(x-A[4])*(x-A[5])*(x-A[6])*(x-A[7])/(Fact(7)*exp(7*ln(hh)))+D[8]*(x-A[1])*(x-A[2])*(x-A[3])*(x-A[4])*(x-A[5])*(x-A[6])*
(x-A[7])*(x-A[8])/(Fact(8)*exp(8*ln(hh)));Write('P(',x:2:4,')=',Pn:2:4); Readln; End.
Метод Симпсона
Program Simpson;
Uses Crt;Var n,a,b,k:integer;
x,x0,xn,h,y,y0,s1,s2,yn,Int,R,M:real;
Function f(x:real):real; Begin
f:=1/(1+sqr(x)); End;
Begin ClrScr; Writeln('Введите количество разбиений n:'); Readln(n);
Writeln('Введите пределы интегрирования a и b:');
Readln(a,b);h:=(b-a)/n;x0:=a; y0:=f(x0);xn:=a+n*h; yn:=f(xn);For k:=1 to n-1 do Begin x:=a+k*h; y:=f(x);
If k mod 2<>0 then s1:=s1+y else s2:=s2+y;
End; Int:=h/3*(y0+4*s1+2*s2+yn); Write('Int=',Int:2:6); Readln; End.
Метод трапеций
Program Trapetsia;
Uses Crt; Var n,k,a,b:integer;
x,x0,xn,h,y,y0,yn,Int,R,M:real;
Function f(x:real):real; Begin
f:=1/(1+sqr(x)); End;Begin
ClrScr; Writeln('Введите количество разбиений n:');
Readln(n);
Writeln('Введите пределы интегрирования a и b:');
Readln(a,b); h:=(b-a)/n; y:=0; For k:=1 to n-1 do
Begin x:=a+k*h; y:=y+f(x); End; x0:=a; y0:=f(x0);
xn:=a+n*h; yn:=f(xn); Int:=h*(y0/2+y+yn/2);
Write('Int=',Int:2:6); M:=abs(f(2)); Readln; End.
Моделирование движения тела в вязкой среде
Program XXX; Uses Graph,Crt;
Var k,m,a,b,t,dt,v,x,x0:Real; gd,gm,i:Integer;
Begin ClrScr; m:=20; k:=100/3e-2; x0:=5e-2;
a:=1e2; b:=1e4; dt:=1e-4; gd:=0;
Initgraph (gd,gm,'E:\pascal\bgi');
v:=0; x:=0.1;SetColor(15);Line(0,225,600,225);
Line(0,305,0,115);Repeat
v:=v-(k*x+a*v+b*v*v*v)*dt/m; x:=x+v*dt;
t:=t+dt;
PutPixel(Round(t*300),225-Round(x*1e3),15);
Until t>=2; Readln; CloseGraph; End.