10 Метод Фридмена
Пусть дан алгебраический многочлен n-ой степени. Для того чтобы из него выделить квадратный трехчлен можно воспользоваться методом Фридмана.
В качестве начального
приближения квадратного трехчлена
берется три последних слагаемых, деленных
на коэффициент при
.
Метод Фридмана:
1 Выделяем квадратный трехчлен.
2 Располагаем
по
убывающим степеням и делим на
.
3 Записываем
в
порядке возрастания степеней и делим
на частное от первого деления.
Результат делиться
на коэффициент при
и получается следующее приближение
.
Далее все повторяется начиная с пункта
2.
12 Метод исключений Гаусса с выбором главного элемента.
Для уменьшения погрешности метод Гаусса модифицируется в метод Гаусса с выбором главного элемента.
Путем перестановок строк или столбцов добиваются того, чтобы на главной диагонали матрицы системы стояли max элементы.
Для практических применений метода Гаусса решение выполняют в виде таблицы.
|
X1 |
X2 |
X3 |
… |
xn |
b |
Σ |
К.с. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Совпадение суммы и контрольной суммы свидетельствует о правильности выполненных действий, если наблюдается расхождение, то где-то допущена вычислительная ошибка.
25. Численное интегрирование. Формулы трапеций Оценка точности
При вычислениях по формулам прямоугольников результаты будут, вообще говоря, тем точнее, чем больше число n отрезков разбиения промежутка интегрирования. Однако увеличение числа n ведёт к усложнению расчётов. Поэтому значительный интерес представляют формулы, дающие более точные результаты при том же числе разбиений.
,
(1)
где
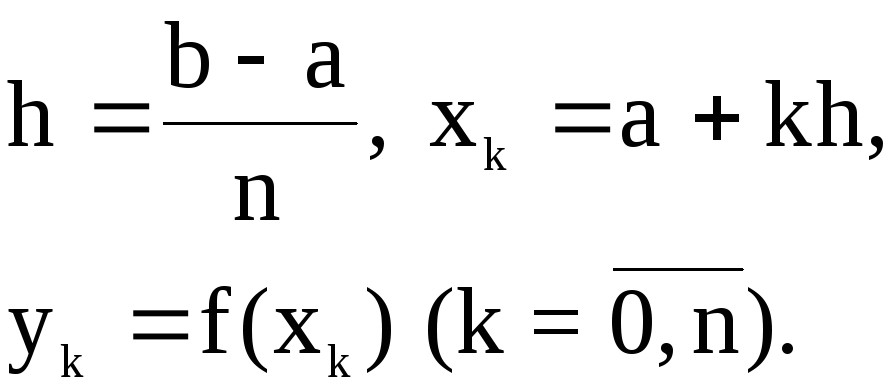(2)
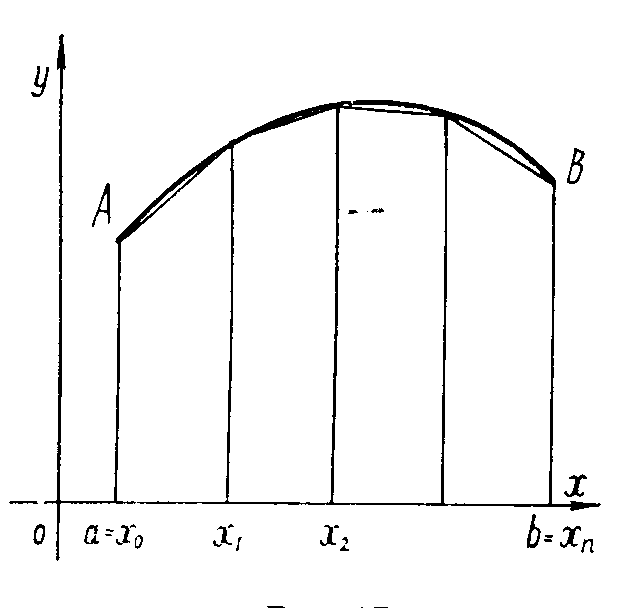
Формула (1) называется
формулой
трапеций;
правая часть её выражает площадь фигуры,
состоящей из трапеций, высота каждой
из которых равна h,
основания –
(рис.1).
Если
– остаточный член приближённой формулы
(1), т.е.
(3)
то
(4)
где
(5)
13 Метод lu-разложения для систем уравнений.
Ax=b, где A – квадратная матрица (n*n). detA≠0
A=LU (представляем в виде произведения нескольких матриц)
L – нижняя треугольная матрица, на главной диагонали которой располагаются единицы.
U – верхняя треугольная матрица.
LUx=b x –? Введем обозначение
Ux=y
Ly= b
Y – неизвестный пока вектор-столбец.
Способ определения элементов матрицы L и U.
Рассмотрим матрицу 3x3.
Пусть имеем матрицу:
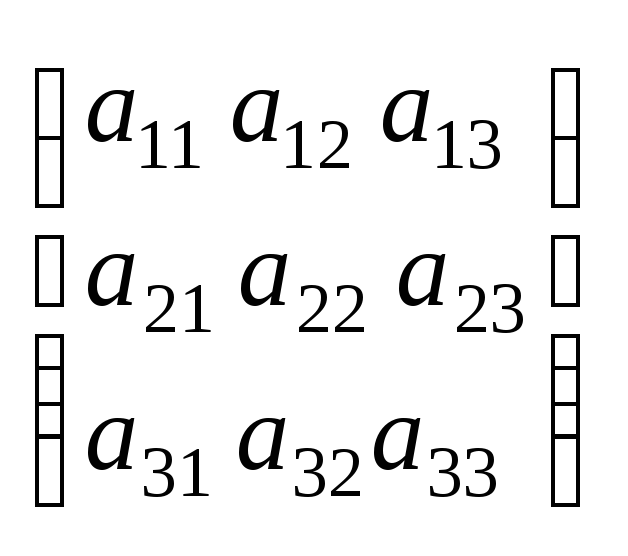
И она имеет вид:
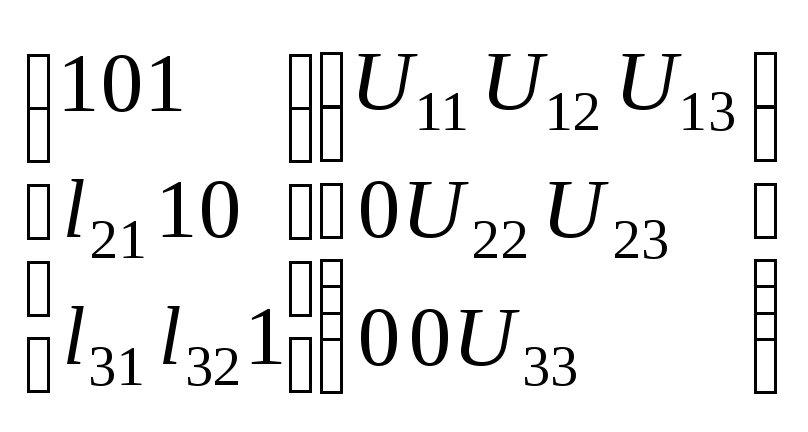
Далее:
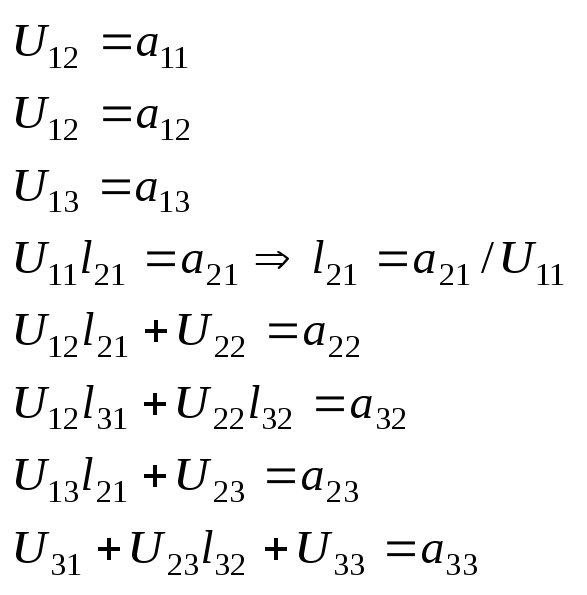
Если матрица А является Эрмитовой, то метод разложения приводится к методу квадратного корня.
Эрмитова матрица – матрица, если она совпадает со своей транспонированной комплексно-сопряженной.
Если матрица А вещественная, то Эрмитова матрица является симметричной. Для сим. матрицы этот метод преобразуется к методу квадратного корня т.е.
D – матрица с элементами диагонали ±1.
S – треугольная матрица.