22.Определение параметров эмпирической формулы методом наименьших квадратов
Идея метода состоит в нахождении приближающей функции
Р(х)=b0+b1х+…+bnхn (1)
из условия минимальности суммы квадратов значений отклонения этой функции в данных точках от табличных значений. Другими словами, необходимо найти коэффициенты выражения (1) из заданного условия.
Сумма равна следующему выражению:
S(b0,b1,….,bn)= (P(xi)-yi)2 (2)
Необходимым условием минимума функции S является равенство нулю ее частных производных. Следовательно, для нахождения коэффициентов получим систему линейных алгебраических уравнений.
S(b0,b1,….,bn)/b0=0
S(b0,b1,….,bn)/b1=0 (3)
S(b0,b1,….,bn)/bn=0
Решив систему (3), найдем искомые коэффициенты.
Затем, необходимо вычислить ошибки приближения по следующим формулам:
O0= P(x0)-y0
O1= P(x1)-y1
…………….
On= P(xn)-yn
8 Итерационные методы решения уравнений с одной переменной (метод хорд).
Пусть f(a)f(b)<0.
Проведем через точки M(a,
f(a))
и N(b,
f(b))
прямую линию(хорду), уравнение которой
записывается в виде
.
Найдем точку пересечения хорды осью
абсцисс:
(*)
За приближенное
значение корня уравнения
примем х1.
Второе приближение х2 вычисляем по формуле (*) относительно того из отрезков [a; x1] и [x1; b], на концах которого функция f(x) принимает значения разных знаков. Аналогично вычисляются и следующие приближения.
Кроме того,
предположим, что вторая производная f
``(x)
на интервале (a;
b)
сохраняет знак. Тогда на (a;
b)
график функции y=
f(x)
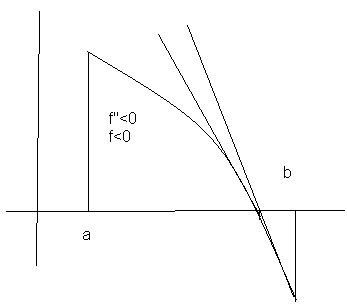
выпуклый, если f//(x)<0,
и лежит выше любой своей хорды. В этом
случае точка пересечения хорды с осью
абсцисс находится между корнем уравнения
и тем концом отрезка [a;
b],
в котором значение функции f(x)
положительно(рис. 1.3.,1.4 ).
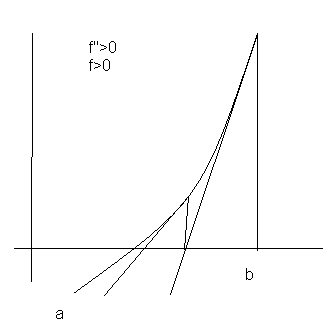
Если же f"(x)>0
,
,
то график функции y=f(x)
на интервале (a;b)
вогнутый и лежит ниже любой своей хорды.
В этом случае точка пересечения хорды
с осью абсцисс находится между корнем
уравнения
и
тем концом отрезка [a;b],
в котором значение f(x)
отрицательно (рис. 1.5, 1.6).
Следовательно, во всех случаях приближенное значение корня лежит между точным его значением и тем концом отрезка, в котором знаки f(x) и f"(x) противоположны.
Поэтому, если известно (n-1)-е приближение корня, то его n-е приближение можно вычислить по формуле
xn=[bf(xn-1)-xn-1f(b)]/[f(xn-1)-f(b)],
для случая f(a)f"(x)<0
или по формуле
xn=[af(xn-1)-xn-1f(a)]/[f(xn-1)-f(a)],
для случая f(b)f"(x)<0.
На практике вычисление приближенных значений продолжают до тех пор, пока два последовательных приближения xn и хn-1 не будут удовлетворять условию
|xn-xn-1|<ε. (1.3)
Но из выполнения неравенства (1.3) не следует , что |x*-xn|<ε,
где х*- искомый корень уравнения.
Более надежным практическим критерием окончания счета является выполнение неравенства
(xn-xn-1)2/|2xn-1-xn-xn-2|<ε. (1.4)
9 Итерационные методы решения уравнений с одной переменной (метод касательных)
Рассмотрим первый вариант:
Для более точной оценки приращения расчётов используется формула:
Пусть функция
.
Пусть
–
некоторое приближение к заданному
корню, тогда
Если пренебречь более высокими порядками, то получим:
