17. Интерполяционный многочлен Ньютона.

Пусть функция f задана таблицей. Построим интерполяционный многочлен , степень которого не больше n и для которого выполнены условия: (1) Будем искать в виде: (2) где - многочлен степени n, причём 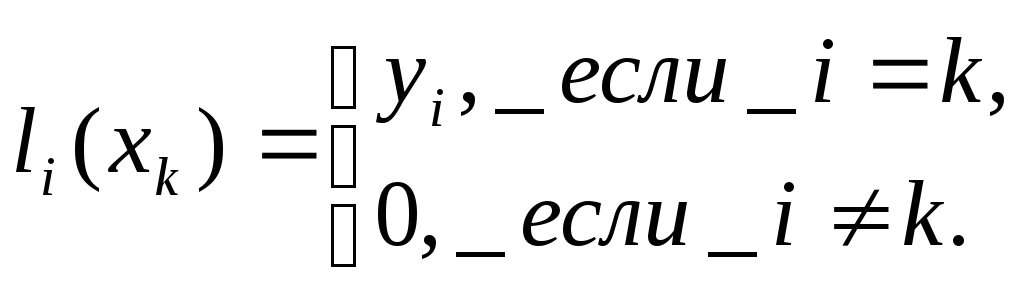(3)

Очевидно, что требование (3) с учётом (2) вполне обеспечивает выполнение условий (1). Многочлены составим следующим способом: (4) где - постоянный коэффициент, значение которого найдём из первой части условия (3): (замечаем, что ни один множитель в знаменателе не равен нулю). Подставим в (4) и далее с учётом (2) окончательно имеем: (5). Это и есть интерполяционный многочлен Лагранжа. По таблице исходной функции f формула (5) позволяет весьма просто составить «внешний вид» многочлена.

15 Итерационные методы (метод Зейделя).

В отличие от метода простой итерации приближение полученные из предыдущих уравнений используется в последующих на каждом шаге итерации.

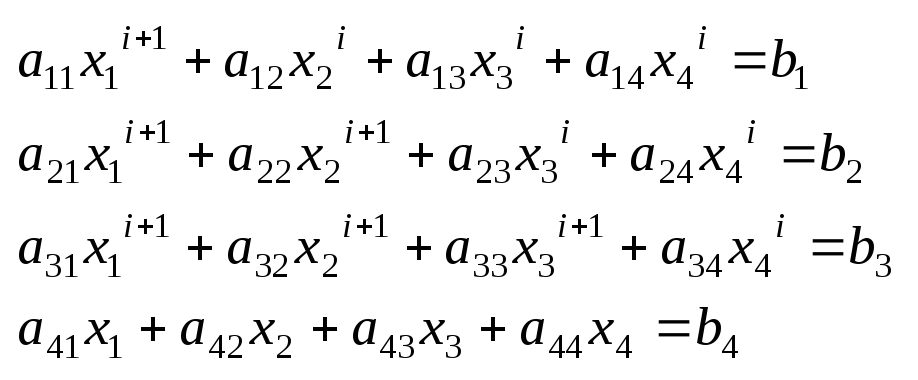В качестве нач. приближения выбирается свободные члены.

Предположим

и т.д.

Получим

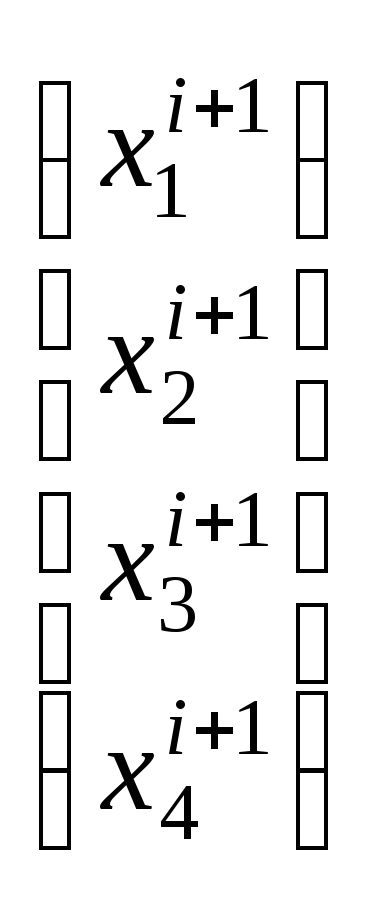
Метод Зейделя обладает более высокой скоростью сходимости по сравнению с методом итерации.

Алгоритм для системы (4.1) можно записать в виде:

(5.1)

где

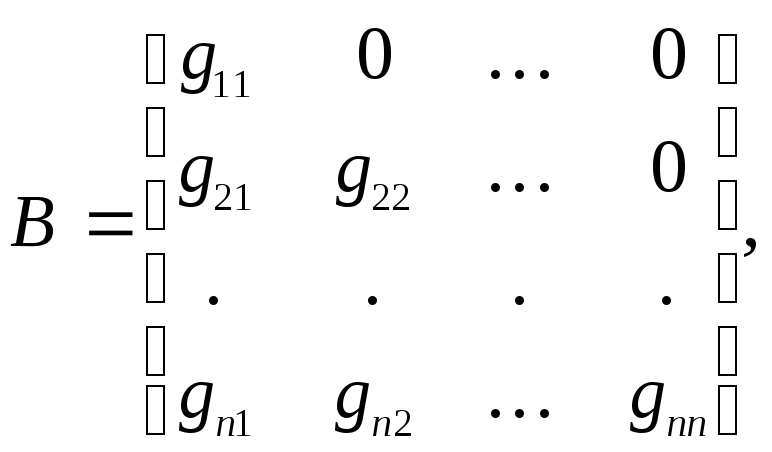
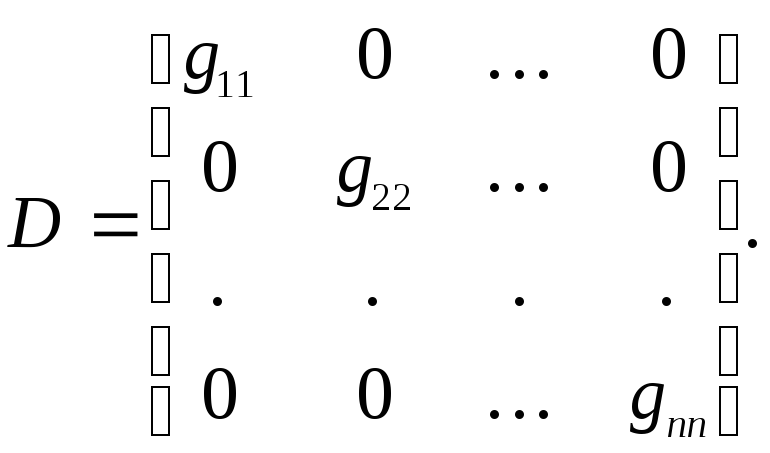
Метод Зейделя можно трактовать как разновидность общего итерационного процесса:

где , . Теперь для сходимости (5.1) необходимо и достаточно выполнение условия и достаточно, чтобы или

Если для одной и той же системы методы итерации и Зейделя сходятся, то метод Зейделя предпочтительнее. Однако области сходимости этих двух методов, вообще говоря, различны. Можно привести примеры, для которых метод итераций сходится, а метод Зейделя не сходится, а наоборот.

20. Понятие о сплайн-интерполировании.

При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для вычислений. Высокой степени многочлена можно избежать, разбив отрезок интерполяции на несколько частей с построением на каждой части самостоятельного интерполяционного многочлена. Однако такое интерполирование приобретает существенный недостаток: в точках стыка разных интерполяционных многочленов будет разрывной их первая производная.

В этом случае удобно пользоваться особым видом кусочно-полиноминальной интерполяции — интерполяции сплайнами (от англ. spline— рейка).

Сплайн — это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными. Рассмотрим способ построения сплайнов третьей степени (так называемых кубических сплайнов), наиболее широко распространенных на практике.

Для каждого отрезка

Получили 4 неизвестных. Для определения коэф-тов используют условия сливания :

при ()

при ()

Должны сливаться 1-е, 2-е, 3-и производные в узлах. Решая систему 4n уравнений опр. Коэф-нты сплайнов. Конечная формула:

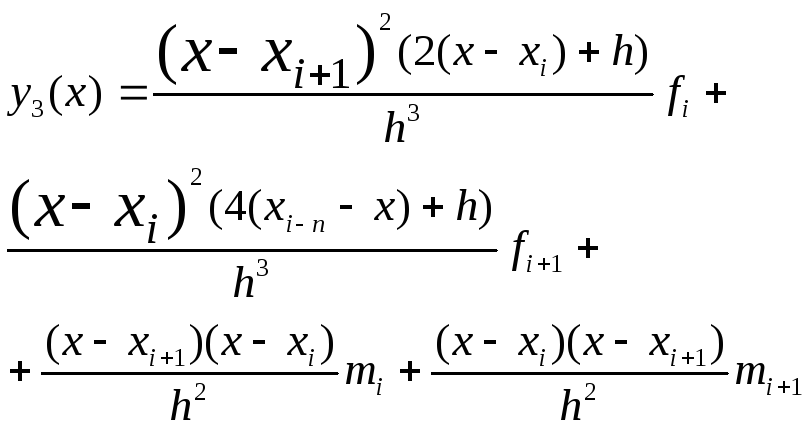
Для случая =отстоящих узлов - значение функции в -м узле.

4. Структура полной погрешности решения задач.

Систематический учёт погрешностей.

Метод предусматривает поэтапный подсчёт границ погрешностей всех промежуточных и окончательного результатов по правилам вычисления погрешностей, рассмотренных выше. Промежуточные результаты, также как и их погрешности, заносятся в специальную расчётную таблицу, состоящую из двух параллельно заполняемых частей – для результатов и их погрешностей

Метод границ.

В случае, когда не столь важно получить наиболее близкое к точному значению вычисляемой величины, сколь важно иметь абсолютно-гарантированные границы её возможных значений применяют метод границ, суть которого в следующем. Для функции из аргументов X и Y необходимо вычислить, где a и b – приближённые значения аргументов, причём совершенно точно известно, что , , где и – соответственно обозначения нижней и верхней границы значений, и тогда

если f возрастает по X иY, и

,

если f возрастает по X и убывает по Y.

В частности, если

, то ;

, то ;

, то ;

, то Расчётная граница метода имеет две строки для вычисления НГ и ВГ выражения.

Правило подсчёта цифр.

При вычислении этим методом составляется обычная расчётная таблица, явный учёт погрешностей не ведётся, округления результатов промежуточных действий проводятся по следующим правилам:

0. при сложении и вычитании приближённых чисел следует округлить число с меньшей абсолютной погрешностью (для десятичных дробей с большим количеством знаков после запятой) так, чтобы в нём осталось на один-два разряда больше, чем в точном числе. В результате считать верными столько десятичных знаков после запятой, сколько их в приближённом данном с наименьшим числом десятичных знаков после запятой;

1. при умножении и делении двух приближённых чисел нужно округлить число с большим количеством значащих цифр так, чтобы в нём было лишь на одну значащую цифру больше, чем в другом числе. В результате считать верными столько значащих цифр, сколько их в приближённом данном с наименьшим числом значащих цифр;

2. в значениях элементарных функций от приближённых значений аргумента (включая возведение в степень, извлечение и т.д.) в результате можно считать верными столько значащих цифр, сколько верных значащих цифр имеет значение аргумента;

3. при записи промежуточных результатов следует сохранять на одну цифру больше, чем рекомендуют правила 1-3. В окончательном результате эта запасная цифра округляется.

16. Задача приближения функций. Постановка задачи интерполирования.

Пусть известные значения некоторой функции f образуют таблицу. При этом требуется получить значение функции f для такого значения аргумента x, которое входит в отрезок [], но не совпадает ни с одним из значений (i=0,1,…,n). Очевидный приём решения этой задачи - вычислить значение , воспользовавшись аналитическим выражением функции f . Этот приём, однако, можно применить лишь в случае, когда аналитическое выражение f пригодно для вычислений. Более того, часто аналитическое выражение функции f вовсе неизвестно. В этих случаях применяется особый приём – построение по исходной информации (см. таблицу) приближающей функции F, которая в некотором смысле близка к функции f и аналитическим выражением которой можно воспользоваться для вычислений, считая приближённо, что (1)

Классический подход к решению задачи построения приближающей функции основывается на требовании строгого совпадения значений и в точках, т.е. (2) В этом случае нахождение приближённой функции называют интерполяцией (или интерполированием), а точки - узлами интерполяции. Будем искать интерполирующую функцию в виде многочлена степени n: . (3) Этот многочлен имеет n+1 коэффициент. Естественно предполагать, что n+1 условия (2), наложенные на многочлен, позволят однозначно определить его коэффициенты. Действительно, требуя для выполнения условий (2), получаем систему n+1 уравнений с n+1 неизвестными: (4) Решая эту систему относительно неизвестных , мы и получим аналитическое выражение полинома (3). Система (4) всегда имеет единственное решение, т.к. её определитель 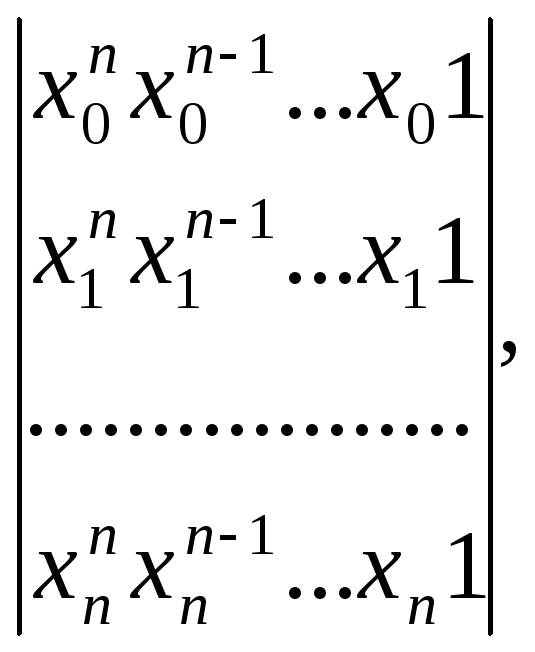известный в алгебре как определитель Вандермонда, отличен от нуля. Отсюда следует, что интерполяционный многочлен для функции , заданной таблицей, существует и единствен (может случиться, что какие-то коэффициенты в , в том числе и , равны нулю; поэтому интерполяционный полином при рассмотренных условиях в общем случае имеет степень, не большую, чем n) . Описанный приём в принципе можно было бы использовать и для практического решения задачи интерполирования многочленом, однако на практике используются другие, более удобные и менее трудоёмкие способы.