
- •Глава 3. Вступ до математичного аналізу
- •§3.1 Числова послідовність. Границя послідовності
- •§3.2 Функція. Границя функції. Теореми про границі. Неперервність функції.
- •3.2.1 Функція. Найпростіші властивості функції
- •3.2.2 Границя функції. Обчислення границь
- •3.2.3 Неперервність функції
- •Глава 4. Диференціальне числення функції однієї змінної
- •§4.1 Означення похідної. Рівняння дотичної. Рівняння нормалі
- •1. Знайдіть похідну функції в точці X, використовуючи означення похідної.
- •4.1.2 Геометричне застосування похідної
- •§4.2 Правило обчислення похідних. Похідна показникової, логарифмічної, тригонометричної, складеної функцій.
- •Знайдіть похідні наступних функції:
- •II. Знайдіть похідну функції в т. :
- •§4.3 Монотонність функції. Локальний екстремум функції. Найбільше і найменше значення функції.
- •4.3.1 Монотонність і екстремум функції
- •4.3.2 Найбільше і найменше значення функції
- •§4.4 Опуклість і вгнутість кривих. Точки перегину. Асимптоти кривої. Дослідження функції та побудова її графіка
- •4.4.1 Опуклість і вгнутість кривих
- •4.4.2 Асимптоти кривої
- •4.4.3 Схема дослідження функції та побудова її графіка
- •Глава 5. Інтегральне числення функції однієї змінної
- •§5.1 Невизначений інтеграл. Основні методи інтегрування невизначеного інтеграла
- •Метод безпосереднього інтегрування
- •5.1.2 Метод підстановки (заміни змінної)
- •5.1.3 Метод інтегрування частинами
- •§5.2 Визначений інтеграл. Методи обчислення визначених інтегралів
- •5.2.1 Визначений інтеграл як границя інтегральної суми
- •5.2.2 Властивості визначеного інтеграла
- •5.2.3 Формула Ньютона-Лейбніца
- •5.2.4 Заміна змінної у визначеному інтегралі (метод підстановки)
- •5.2.5 Метод інтегрування частинами
- •§5.3 Деякі застосування визначеного інтеграла: обчислення площ плоских фігур
- •Глава 6. Диференціальне числення функції багатьох змінних
- •§ 6.1 Означення функцій багатьох змінних. Частинні похідні функції багатьох змінних
- •6.1.1 Функція багатьох змінних. Область визначення. Лінії та поверхні рівня
- •6.1.2 Границя та неперервність функції
- •6.1.3 Частинні похідні першого порядку
- •6.1.4 Похідні та диференціали вищих порядків
- •§ 6.2 Повний диференціал функції багатьох змінних та його застосування
- •6.2.1 Повний диференціал функції та його застосування до обчислення значень функцій та похибок
- •Vі. Обчислити наближено:
- •Глава 7. Диференціальні рівняння
- •§ 7.1 Диференціальні рівняння першого порядку. Задача Коші. Загальний і частинний розв’язок диференціального рівняння першого порядку
- •7.1.1 Загальні поняття та означення. Геометричний зміст диференціального рівняння
- •§ 7.2 Диференціальні рівняння першого порядку з відокремлюваними змінними. Однорідні диференціальні рівняння першого порядку
- •7.2.1 Диференціальні рівняння першого порядку з відокремлюваними змінними
- •7.2.2 Однорідні диференціальні рівняння
- •§ 7.3 Лінійні диференціальні рівняння першого порядку. Диференціальні рівняння вищих порядків
- •7.3.1 Лінійні диференціальні рівняння першого порядку
- •7.3.2 Диференціальні рівняння вищих порядків
- •§7.4 Лінійні однорідні диференціальні рівняння другого порядку з постійними коефіцієнтами
- •Глава 8. Ряди
- •§ 8.1 Числові ряди. Найпростіші властивості числових рядів
- •8.1.1 Основні поняття. Необхідна умова збіжності ряду
- •§ 8.2 Знакододатні ряди. Достатні ознаки збіжності
- •§ 8.3Степеневі ряди Теорема Абеля. Інтеграл та радіус збіжності степеневого ряду
- •8.3.1 Поняття степеневого ряду. Теорема Абеля
- •§ 8.4 Ряд Тейлора. Розкладання елементарних функцій у ряд Маклорена
- •8.4.1 Розвинення елементарних функцій у ряди Тейлора і Маклорена. Наближені обчислення
- •§8. 5 Ряди Фур’є
- •8.5.1Тригонометричні ряди
- •8.5.2 Ортогональність системи функцій
- •Відповіді
- •Глава 5.
- •Глава 6.
- •Глава 7
- •Список рекомендованої літератури
- •Вища математика Збірник задач іі частина
Глава 7. Диференціальні рівняння
§ 7.1 Диференціальні рівняння першого порядку. Задача Коші. Загальний і частинний розв’язок диференціального рівняння першого порядку
7.1.1 Загальні поняття та означення. Геометричний зміст диференціального рівняння
Диференціальним рівнянням першого порядку називається рівняння виду
![]() ,
(1)
,
(1)
яке
пов’язує незалежну змінну
![]() ,
невідому функцію
,
невідому функцію
![]() та її похідну.
та її похідну.
Розв’язком диференціального рівняння (1) на деякому
інтервалі
![]() називається диференційована на цьому
інтервалі функція
називається диференційована на цьому
інтервалі функція
![]() ,
яка при підстановці в рівняння (1)
,
яка при підстановці в рівняння (1)
перетворює
його в тотожність по
![]() на
на
![]() .
.
Функція
![]() ,
яка залежить від аргументу і довільної
сталої
,
яка залежить від аргументу і довільної
сталої
![]() ,
називається загальним
розв’язком рівняння(1)
в області
,
називається загальним
розв’язком рівняння(1)
в області
![]() ,
якщо вона задовольняє дві умови:
,
якщо вона задовольняє дві умови:
1) функція
![]() є розв’язком
рівняння при будь-якому значенні сталої
є розв’язком
рівняння при будь-якому значенні сталої
![]() з деякої множини;
з деякої множини;
2) для
довільної точки
![]() можна знайти таке значення
можна знайти таке значення
![]() ,
що функція
,
що функція
![]() задовольняє початкову умову:
задовольняє початкову умову:
![]() .
.
Частинним розв’язком рівняння (1) називається функція
![]() ,
яка утворюється із загального розв’язку
,
яка утворюється із загального розв’язку
![]() при певному значенні сталої
при певному значенні сталої
![]() .
.
Якщо
загальний розв’язок диференціального
рівняння знайдено в неявному вигляді,
тобто у вигляді рівняння
![]() ,
то такий розв’язок називають загальним
інтегралом диференціального рівняння
(1).
Рівність
,
то такий розв’язок називають загальним
інтегралом диференціального рівняння
(1).
Рівність
![]() називають частинним
інтегралом рівняння.
називають частинним
інтегралом рівняння.
І.
Перевірити, чи є розв’язками
даних диференціальних рівнянь указані
функції.
![]() :
:
-
 ,
,
 ;
; -
 ,
,
 ;
; -
 ,
,
 ;
; -
 ,
,
 ;
; -
 ,
,
 ;
; -
 ,
,
 .
.
ІІ.
Довести, що для даних диференціальних
рівнянь указані функції є розв’язком
при будь-якому значенні
![]() ,
і знайти частинні розв’язки, що
задовольняють початковим умовам:
,
і знайти частинні розв’язки, що
задовольняють початковим умовам:
-
 ,
,
 ,
,
 .
. -
 ,
,
 ,
,
 .
.
ІІІ. Чи є слідуючі функції
а)![]() ;
a)
;
a)
![]() ;
;
1. b)
![]() ;
2.
b)
;
2.
b)
![]() ;
;
c)
![]() ;
c)
;
c)
![]() .
.
розв’зком рівнянь:
-
 . 2.
. 2.
 .
.
ІV.
Знайти значення
![]() , при яких задана функція є розв’язком
рівняння:
, при яких задана функція є розв’язком
рівняння:
1.
![]() ,
,
![]() ;
;
2.
![]() ,
,
![]() .
.
§ 7.2 Диференціальні рівняння першого порядку з відокремлюваними змінними. Однорідні диференціальні рівняння першого порядку
7.2.1 Диференціальні рівняння першого порядку з відокремлюваними змінними
Рівняння виду
![]() ,
(1)
,
(1)
де
![]() і
і
![]() - задані і неперервні на деякому інтервалі
функції, називається диференціальним
рівнянням з відокремлюваними змінними.
- задані і неперервні на деякому інтервалі
функції, називається диференціальним
рівнянням з відокремлюваними змінними.
Рівняння виду
![]()
![]() (2)
(2)
називається диференціальним рівнянням з відокремленими змінними.
Загальний інтеграл диференціального рівняння (2) має вигляд
![]() .
.
Диференціальне рівняння (1) є окремим випадком рівняння виду
![]() .
.
Для
відокремлення змінних у цьому рівнянні
досить обидві його частини поділити на
функцію
![]() .
При цьому втрачаємо розв’язки
.
При цьому втрачаємо розв’язки
![]() ,
,
![]() .
.
7.2.2 Однорідні диференціальні рівняння
Функція
![]() називається однорідною функцією
називається однорідною функцією
![]() -го
виміру відносно змінних
-го
виміру відносно змінних
![]() та
та
![]() ,
якщо для довільного
,
якщо для довільного
![]() виконується тотожність
виконується тотожність
![]() . (1)
. (1)
Диференціальне рівняння
![]() (2)
(2)
називається однорідним, якщо функція * є однорідною функцією нульового виміру.
Підстановкою
![]() ,
,
![]() ,
,
![]() ,
,
де
![]() - невідома функція, рівняння (2) зводиться
до рівняння з відокремленими змінними
- невідома функція, рівняння (2) зводиться
до рівняння з відокремленими змінними
![]() .
.
Рівняння виду
![]() ,
,
де
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() - задані сталі, зводиться до однорідного
рівняння
- задані сталі, зводиться до однорідного
рівняння
змінною
![]() ,
,
![]() ,
якщо
,
якщо
![]() .
Числа
.
Числа
![]() і
і
![]() знаходяться із систем рівнянь
знаходяться із систем рівнянь

І. Знайти загальний розв’язок рівняння:
-
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 .
.
ІІ. Знайти частинні розв’язки рівнянь:
-
 ,
якщо
,
якщо
 ,
при
,
при
 ;
; -
 ,
якщо
,
якщо
 ,
при
,
при
 ;
; -
 ,
якщо
,
якщо
 ,
при
,
при
 ;
; -
 ,
якщо
,
якщо
 ,
при
,
при
 ;
;
-
 ,
якщо
,
якщо
 ,
при
,
при
 .
.
ІІІ. Розв’язати рівняння:
-
 ;
; -
 ;
; -
 ;
; -
 ;
; -
 ;
;
ІV. Знайти частинні розв’язки рівнянь:
-
 ,
якщо
,
якщо
 ,
при
,
при
 ;
; -
 ,
якщо
,
якщо
 ,
при
,
при
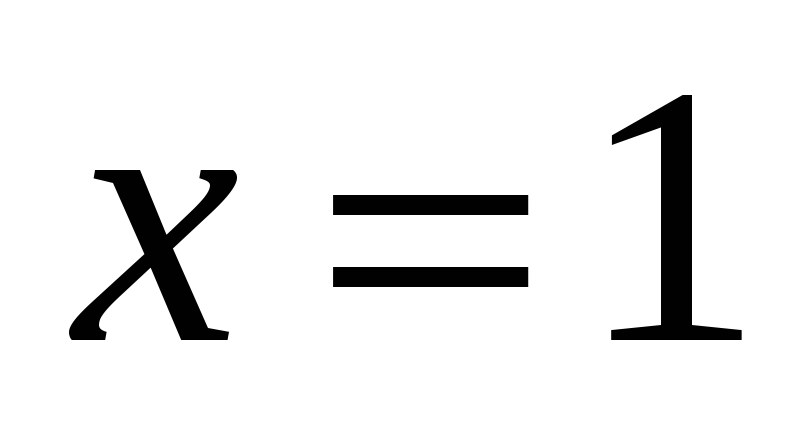 ;
; -
 ,
якщо
,
якщо
 ,
при
,
при
 ;
; -
 ,
якщо
,
якщо
 ,
при
,
при
 ;
; -
 ,
якщо
,
якщо
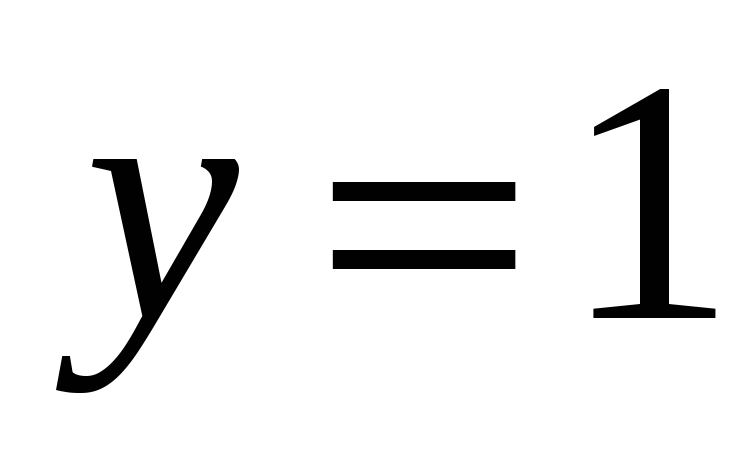 ,
при
,
при
 .
.
