6.1.3 Частинні похідні першого порядку

Якщо існує границя

,

то вона називається частинною похідною функції в точці по змінній і позначається одним із таких символів:

, , , .

Зазначена вище границя обчислюється при умові, що змінна вважається сталою. Аналогічно означається частинна похідна по змінній :

.

Щоб знайти частинну похідну функції змінних , досить обчислити звичайну похідну функції по змінній , вважаючи решту змінних сталими.

6.1.4 Похідні та диференціали вищих порядків

Частинними похідними другого порядку функції називаються їх частинні похідні від частинних похідних першого порядку.

Позначення частинних похідних другого порядку:

; ;

; .

Аналогічно означають і позначаються похідні вищих порядків, наприклад:

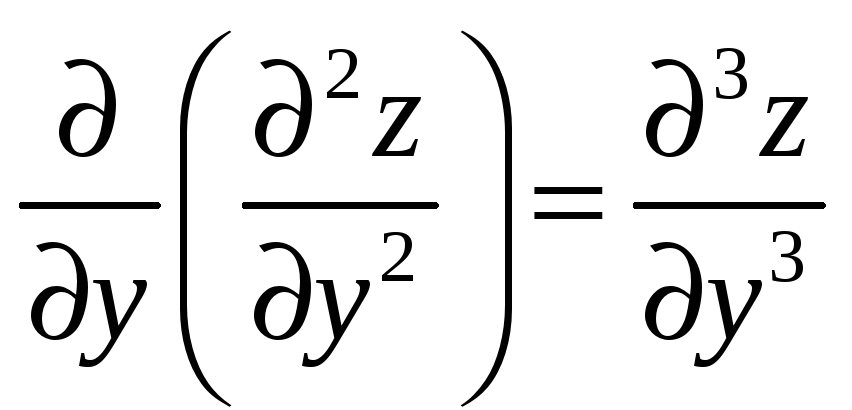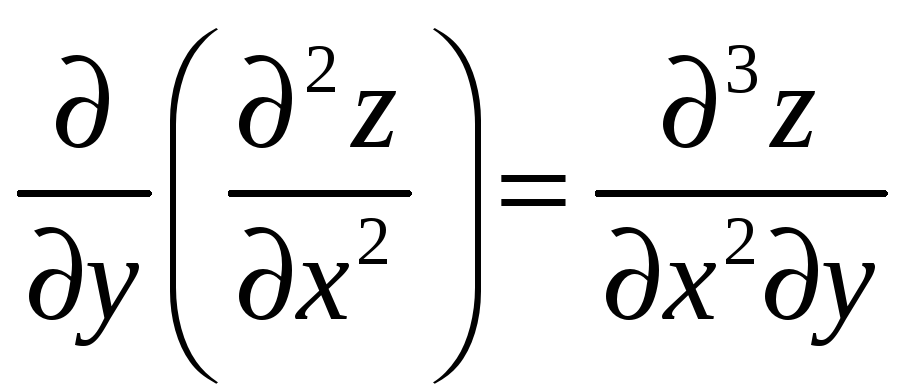; і т. д.

Частинні похідні, які відмінні одна від одної лише порядком диференціювання, називаються мішаними похідними; вони є рівними між собою при умові, що вони неперервні в деякому околі точки . Наприклад,

.

Якщо є функцією незалежних змінних і , то диференціал -го порядку функції означається згідно з формулою

.

Наприклад,

.

Зручно користуватися символічною формулою

.

І. Знайти частинні похідні першого порядку для функцій:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. .

ІІ. Знайти частинні похідні другого порядку для функції:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. .

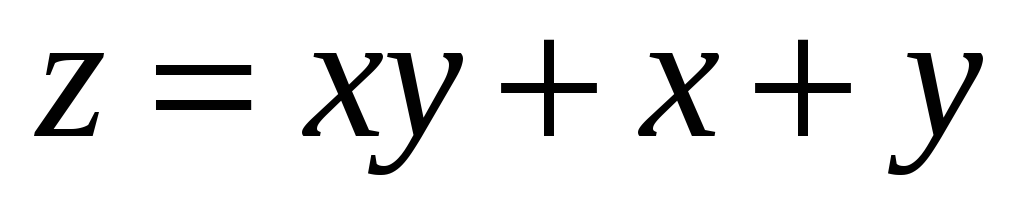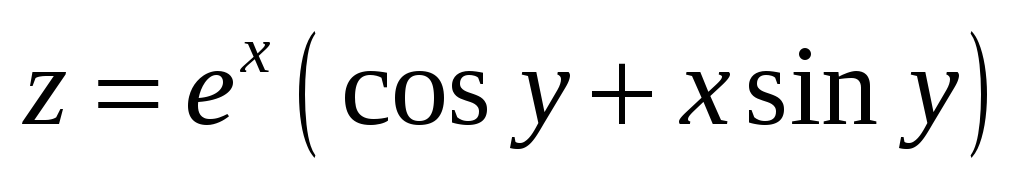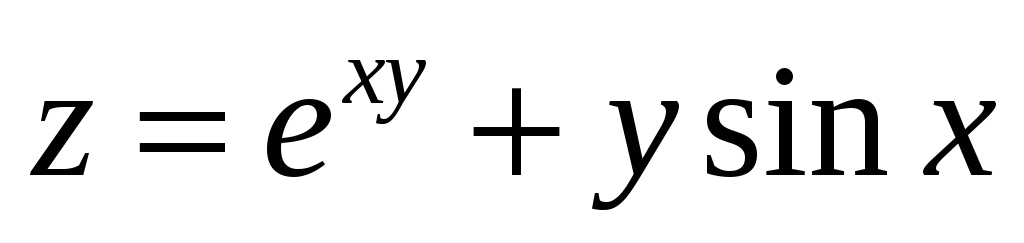ІІІ. Обчислити частинні похідні третього порядку для функції:

1. .

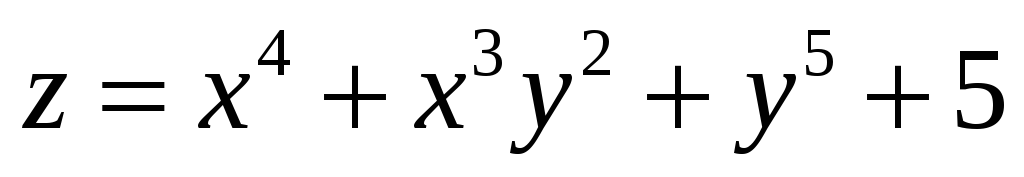ІV. Знайти частинні похідні і в т. :

1. , в ;

2. , в .

§ 6.2 Повний диференціал функції багатьох змінних та його застосування

6.2.1 Повний диференціал функції та його застосування до обчислення значень функцій та похибок

Функція називається диференційованою в точці , якщо її повний приріст можна подати у вигляді

,

де та – дійсні числа, що не залежать від та , і - нескінченно малі при і функції. Повним диференціалом функції називається головна лінійна частина приросту функції, яка обчислюється за формулою

,

де , .

Аналогічна формула вірна для диференційованої функції трьох змінних :

.

Для наближеного обчислення значення функції, наприклад, двох змінних користуються наближеною рівністю

.

Максимальна абсолютна похибка змінної обчислюється за формулою

,

де - максимальна абсолютна похибка змінної .

Максимальну відносну похибку зручно оцінювати

за формулою .

І. Знайти повний диференціал функцій:

1. ; 2. ;

3. ; 4. ;

5. ; 6. ;

7. ; 8. ;

9. ; 10.

11. ; 12. .

13. . 14. .

15. . 16. .

17. . 18..

ІІ. Знайти значення повного диференціала функції:

, при , , , .

ІІІ. Знайти повний диференціал функції , обчислити його значення при , , , , , . Знайти абсолютну і відносну похибку наближення: і .

Vі. Обчислити наближено:

1. .

2. .

3. .

4. .

5. .

6. .

7. .
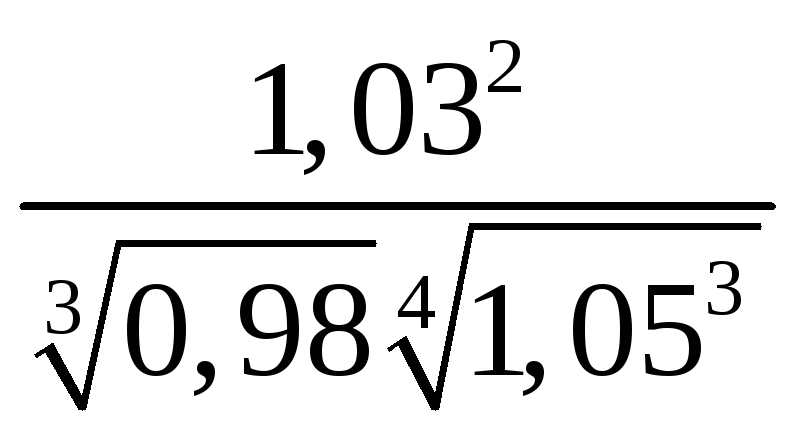