
- •Глава 3. Вступ до математичного аналізу
- •§3.1 Числова послідовність. Границя послідовності
- •§3.2 Функція. Границя функції. Теореми про границі. Неперервність функції.
- •3.2.1 Функція. Найпростіші властивості функції
- •3.2.2 Границя функції. Обчислення границь
- •3.2.3 Неперервність функції
- •Глава 4. Диференціальне числення функції однієї змінної
- •§4.1 Означення похідної. Рівняння дотичної. Рівняння нормалі
- •1. Знайдіть похідну функції в точці X, використовуючи означення похідної.
- •4.1.2 Геометричне застосування похідної
- •§4.2 Правило обчислення похідних. Похідна показникової, логарифмічної, тригонометричної, складеної функцій.
- •Знайдіть похідні наступних функції:
- •II. Знайдіть похідну функції в т. :
- •§4.3 Монотонність функції. Локальний екстремум функції. Найбільше і найменше значення функції.
- •4.3.1 Монотонність і екстремум функції
- •4.3.2 Найбільше і найменше значення функції
- •§4.4 Опуклість і вгнутість кривих. Точки перегину. Асимптоти кривої. Дослідження функції та побудова її графіка
- •4.4.1 Опуклість і вгнутість кривих
- •4.4.2 Асимптоти кривої
- •4.4.3 Схема дослідження функції та побудова її графіка
- •Глава 5. Інтегральне числення функції однієї змінної
- •§5.1 Невизначений інтеграл. Основні методи інтегрування невизначеного інтеграла
- •Метод безпосереднього інтегрування
- •5.1.2 Метод підстановки (заміни змінної)
- •5.1.3 Метод інтегрування частинами
- •§5.2 Визначений інтеграл. Методи обчислення визначених інтегралів
- •5.2.1 Визначений інтеграл як границя інтегральної суми
- •5.2.2 Властивості визначеного інтеграла
- •5.2.3 Формула Ньютона-Лейбніца
- •5.2.4 Заміна змінної у визначеному інтегралі (метод підстановки)
- •5.2.5 Метод інтегрування частинами
- •§5.3 Деякі застосування визначеного інтеграла: обчислення площ плоских фігур
- •Глава 6. Диференціальне числення функції багатьох змінних
- •§ 6.1 Означення функцій багатьох змінних. Частинні похідні функції багатьох змінних
- •6.1.1 Функція багатьох змінних. Область визначення. Лінії та поверхні рівня
- •6.1.2 Границя та неперервність функції
- •6.1.3 Частинні похідні першого порядку
- •6.1.4 Похідні та диференціали вищих порядків
- •§ 6.2 Повний диференціал функції багатьох змінних та його застосування
- •6.2.1 Повний диференціал функції та його застосування до обчислення значень функцій та похибок
- •Vі. Обчислити наближено:
- •Глава 7. Диференціальні рівняння
- •§ 7.1 Диференціальні рівняння першого порядку. Задача Коші. Загальний і частинний розв’язок диференціального рівняння першого порядку
- •7.1.1 Загальні поняття та означення. Геометричний зміст диференціального рівняння
- •§ 7.2 Диференціальні рівняння першого порядку з відокремлюваними змінними. Однорідні диференціальні рівняння першого порядку
- •7.2.1 Диференціальні рівняння першого порядку з відокремлюваними змінними
- •7.2.2 Однорідні диференціальні рівняння
- •§ 7.3 Лінійні диференціальні рівняння першого порядку. Диференціальні рівняння вищих порядків
- •7.3.1 Лінійні диференціальні рівняння першого порядку
- •7.3.2 Диференціальні рівняння вищих порядків
- •§7.4 Лінійні однорідні диференціальні рівняння другого порядку з постійними коефіцієнтами
- •Глава 8. Ряди
- •§ 8.1 Числові ряди. Найпростіші властивості числових рядів
- •8.1.1 Основні поняття. Необхідна умова збіжності ряду
- •§ 8.2 Знакододатні ряди. Достатні ознаки збіжності
- •§ 8.3Степеневі ряди Теорема Абеля. Інтеграл та радіус збіжності степеневого ряду
- •8.3.1 Поняття степеневого ряду. Теорема Абеля
- •§ 8.4 Ряд Тейлора. Розкладання елементарних функцій у ряд Маклорена
- •8.4.1 Розвинення елементарних функцій у ряди Тейлора і Маклорена. Наближені обчислення
- •§8. 5 Ряди Фур’є
- •8.5.1Тригонометричні ряди
- •8.5.2 Ортогональність системи функцій
- •Відповіді
- •Глава 5.
- •Глава 6.
- •Глава 7
- •Список рекомендованої літератури
- •Вища математика Збірник задач іі частина
Глава 4. Диференціальне числення функції однієї змінної
§4.1 Означення похідної. Рівняння дотичної. Рівняння нормалі
4.1.1 Похідна
Похідною
функції
![]() у точці
у точці
![]() називається границя
називається границя
![]() ,
,
де
![]() - приріст аргументу, а
- приріст аргументу, а
![]() - приріст функції.
- приріст функції.
Позначається
похідна через
![]() ,
або
,
або
![]() ,
або
,
або
![]() .
Отже,
.
Отже,
![]() ,
або
,
або
![]() .
.
Значення
похідної функції
![]() при
при
![]() дорівнює кутовому коефіцієнту дотичної,
проведеної до графіка функції у точці
з абсцисою
дорівнює кутовому коефіцієнту дотичної,
проведеної до графіка функції у точці
з абсцисою
![]() ,
тобто
,
тобто
![]() .
.
З погляду фізики похідна має таке тлумачення:
а)
швидкість руху
![]() ,
де
,
де
![]() - шлях,
- шлях,
![]() - час;
- час;
б)
лінійна густина
![]() ,
де
,
де
![]() - маса стержня,
- маса стержня,
![]() - довжина;
- довжина;
в) сила
струму
![]() ,
де
,
де
![]() – кількість електрики, що проходить
через провідник,
– кількість електрики, що проходить
через провідник,
![]() - час;
- час;
г)
теплоємність
![]() ,
де
,
де
![]() – кількість теплоти;
– кількість теплоти;
![]() -температура.
-температура.
Односторонні похідні позначаються відповідно так:
Ліва
похідна
![]() ;
;
Права
похідна
![]() .
.
Якщо обидві ці границі існують і рівні між собою, то тільки в цьому випадку кажуть, що в цій точці існує похідна:
![]() .
.
1. Знайдіть похідну функції в точці X, використовуючи означення похідної.
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
2. Скласти
рівняння дотичної і нормалі до кривої
![]() в т. А(2;8). Знайти довжини відрізків
дотичної
і нормалі в цій точці.
в т. А(2;8). Знайти довжини відрізків
дотичної
і нормалі в цій точці.
3. Скласти
рівняння дотичної і нормалі до параболи
![]() в т. (2;4). Знайти довжини піддотичної і
піднормалі в цій точці.
в т. (2;4). Знайти довжини піддотичної і
піднормалі в цій точці.
4. Написати
рівняння дотичної і нормалі до функції
![]() в точці
в точці
![]() :
:
а)
![]() ;
т.
;
т.
![]() ;
;
б)
![]() ;
т.
;
т.
![]() .
.
5.
У
якій точці дотична до кривої
![]() нахилена до осі Ох під кутом, величина
якого дорівнює
нахилена до осі Ох під кутом, величина
якого дорівнює
![]() ?
?
6. Під яким
кутом дотична до кривої
![]() в точці (0;1) перетинає вісь Ох?
в точці (0;1) перетинає вісь Ох?
7. У параболи
![]() проведена дотична в точці:
проведена дотична в точці:
а) (0;0);
б) (2;1);
в) (4;0).
Знайти величину кута нахилу до дотичної до осі Ох.
4.1.2 Геометричне застосування похідної
Рівняння
дотичної до графіка функції
![]() у
точці
у
точці
![]() має вигляд
має вигляд
![]() ,
,
а рівняння нормалі
![]() .
.
Довжина дотичної
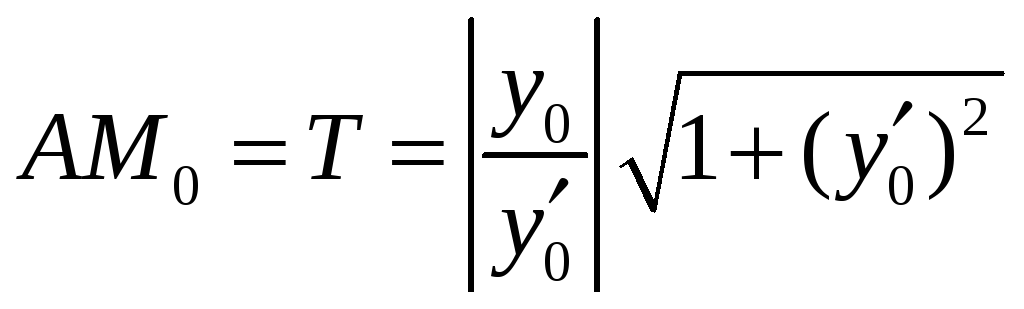 ;
;
довжина нормалі
![]() ;
;
довжина піддотичної
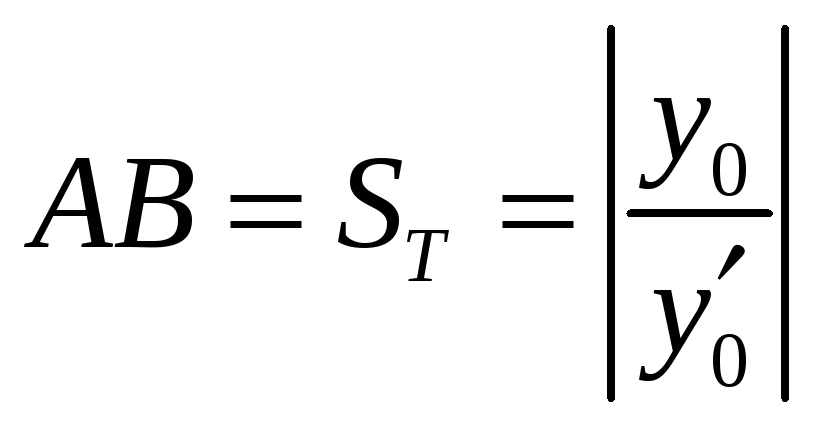 ;
;
довжина піднормалі
![]() .
.
§4.2 Правило обчислення похідних. Похідна показникової, логарифмічної, тригонометричної, складеної функцій.
Основні
правила диференціонування. Вважаємо,
що
![]() - стала величина, а
- стала величина, а
![]() і
і
![]() - деякі диференційовні функції від
- деякі диференційовні функції від
![]() .
.
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
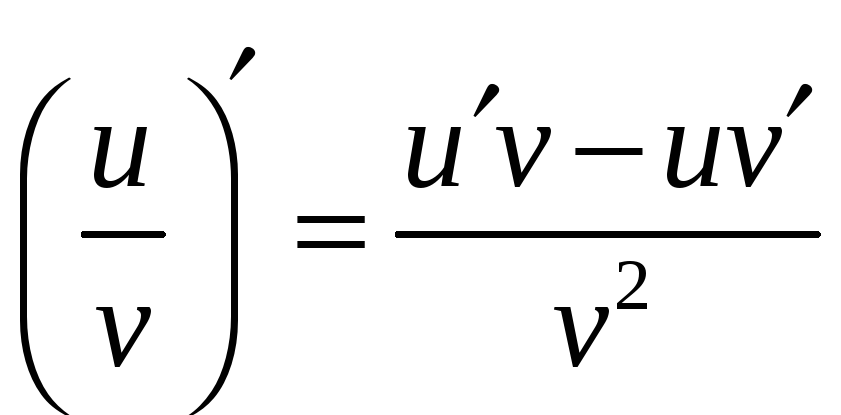 .
.
5. Якщо
![]() ,
де
,
де
![]() ,
то
,
то
![]() ,
або
,
або
![]() .
.
6.
Якщо
![]() ,
а
,
а
![]() ,
то
,
то
![]() .
.
7.
Якщо
![]() ,
то
,
то
![]() .
.
Таблиця похідних.
1.
![]() . 2.
. 2.
![]() .
.
3.
![]() . 4.
. 4.
![]() .
.
5.
![]() . 6.
. 6.
![]() .
.
7.
![]() . 8.
. 8.
![]() . 9.
. 9.
![]() .
.
10.![]() . 11.
. 11.
![]() . 12.
. 12.![]() . 13.
. 13.
![]() . 14.
. 14.
![]() . 15.
. 15.
![]() . 16.
. 16.
![]() . 17.
. 17.
![]() .
.
18.
![]() .
.
-
Знайдіть похідні наступних функції:
1.
![]() ; 2.
; 2.
![]() ;
;
3.
![]() ; 4.
; 4.
![]() ;
;
5.
![]() ; 6.
; 6.
![]() ;
;
7.
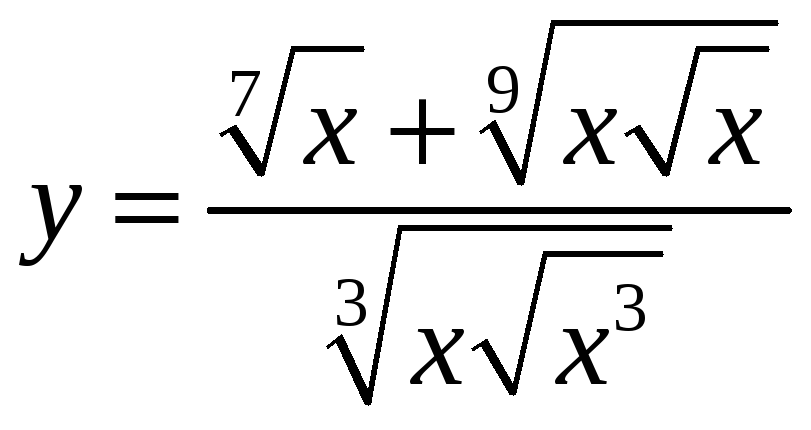 ; 8.
; 8.
![]() ;
;
9.
![]() ;
10.
;
10.
![]() ;
;
11.
![]() ;
12.
;
12.
![]() ;
;
13.
![]() ;
14.
;
14.
![]() ;
;
15.
![]() .
.
II. Знайдіть похідну функції в т. :
-
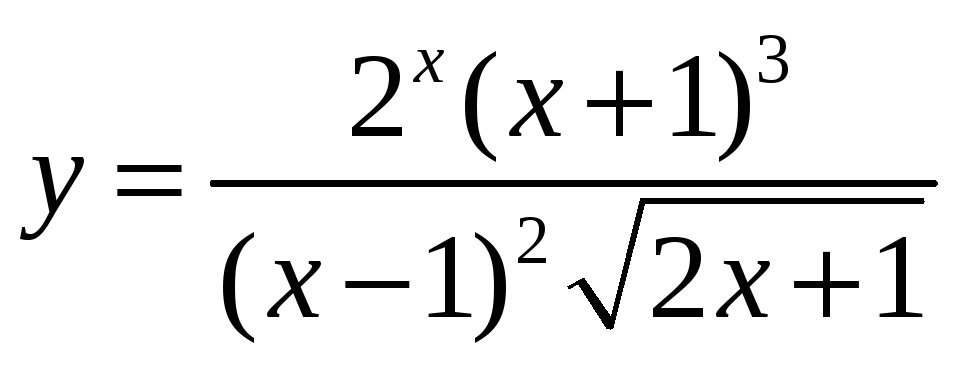 ,
,
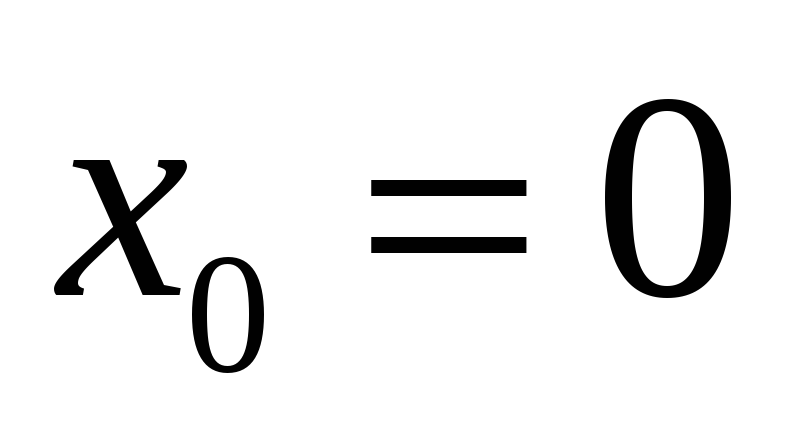 ;
; -
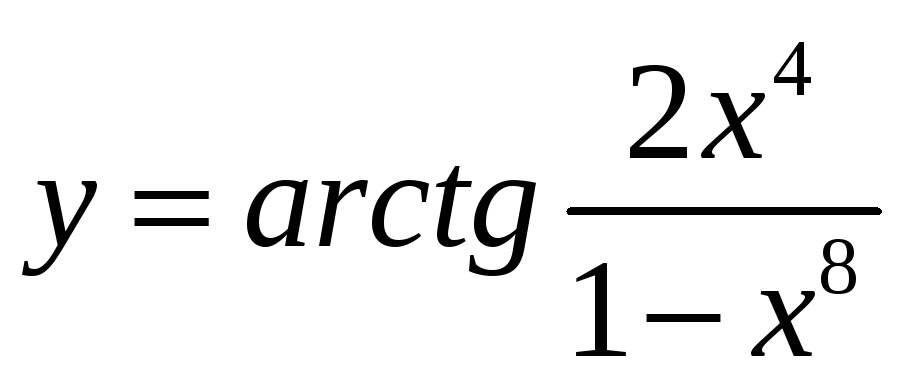 ,
,
 ;
;
-
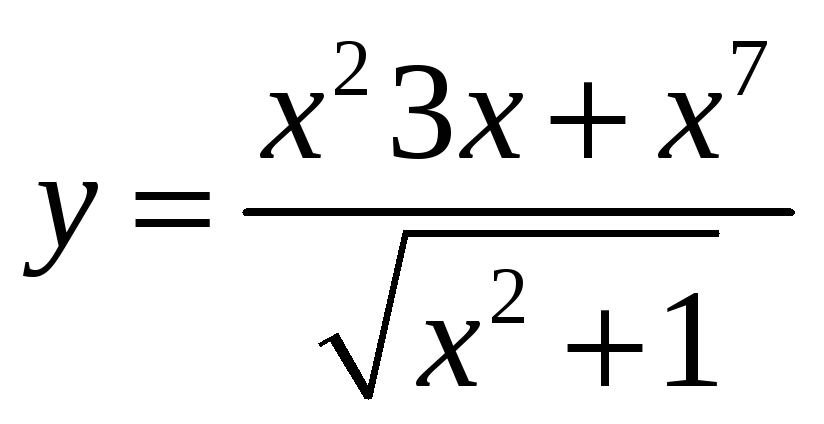 ,
,
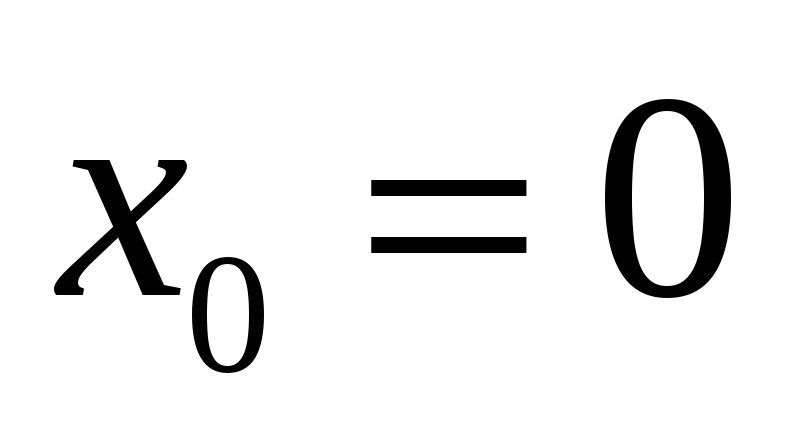 ;
; -
 ,
,
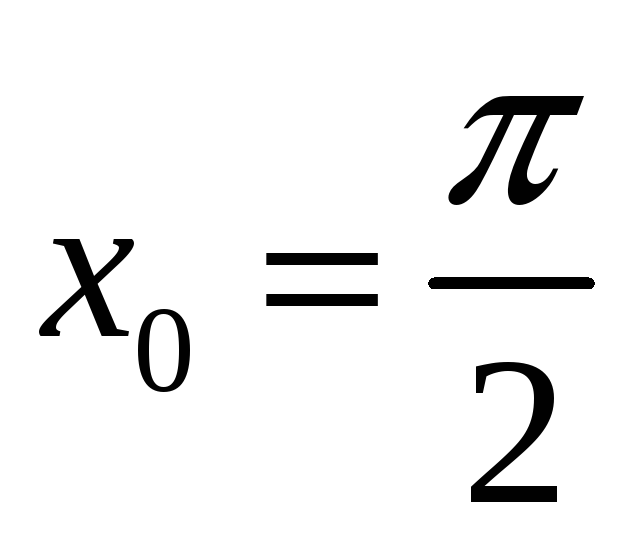 ;
; -
 ,
,
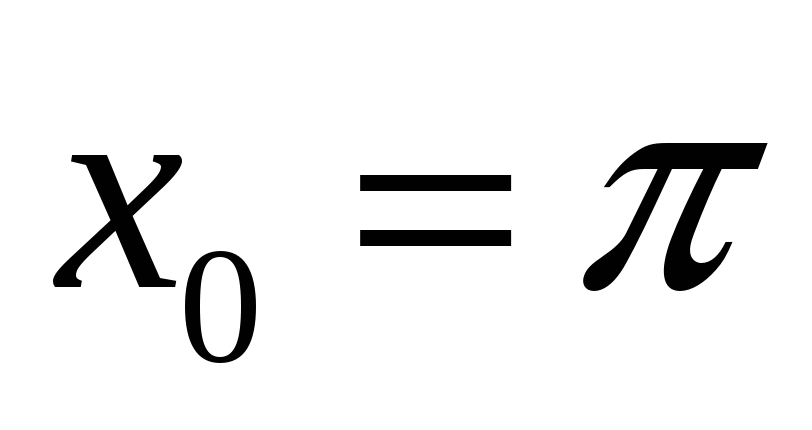 ;
; -
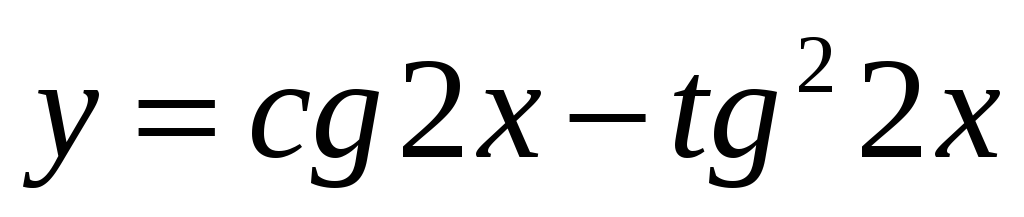 ,
,
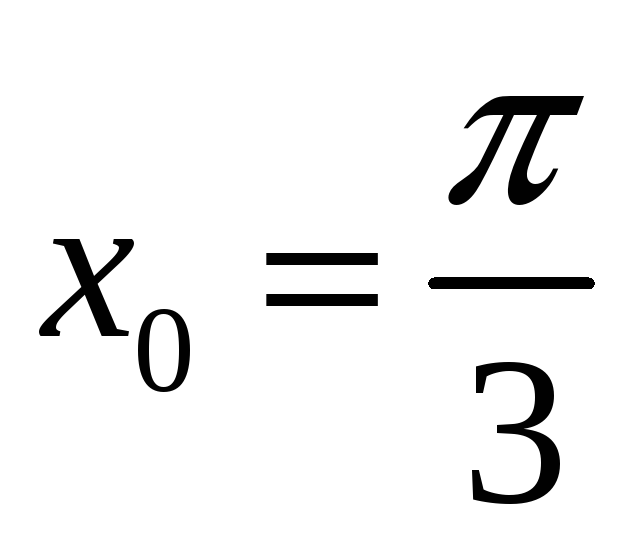 ;
; -
 ,
,
 ;
; -
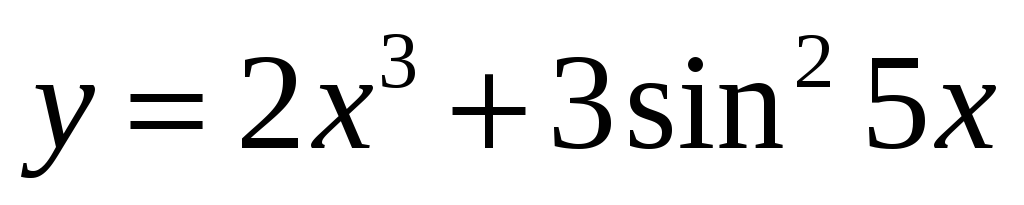 ,
,
 ;
; -
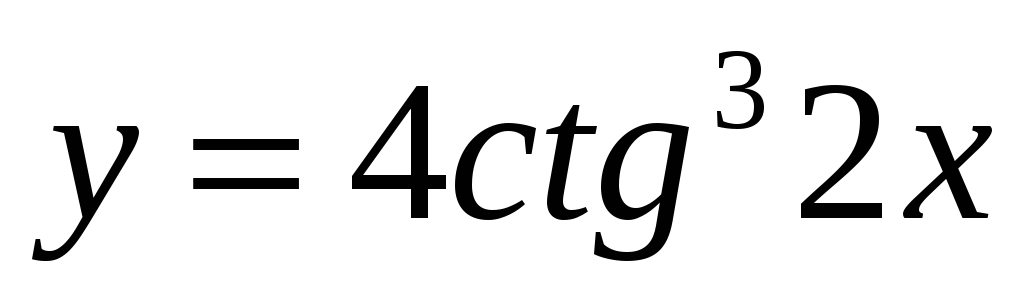 ,
,
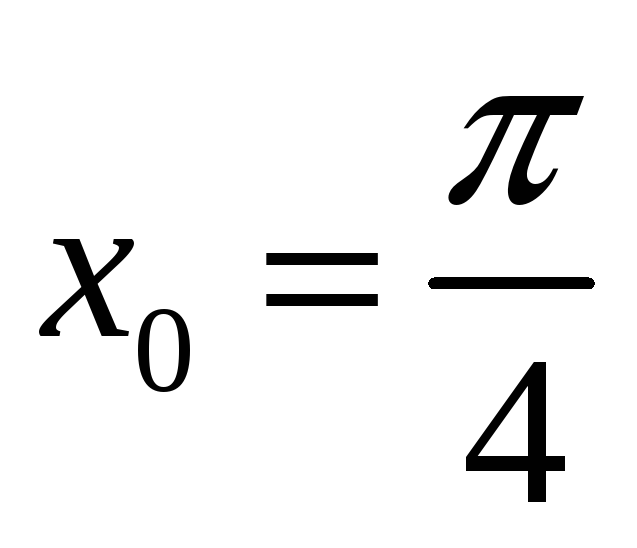 .
.
§4.3 Монотонність функції. Локальний екстремум функції. Найбільше і найменше значення функції.
4.3.1 Монотонність і екстремум функції
Якщо
![]() для
для
![]() ,
то функція
,
то функція
![]() на цьому інтервалі зростає (спадає).
на цьому інтервалі зростає (спадає).
Якщо
функція
![]() в точці
в точці
![]() має екстремум, то її похідна в цій точці
обертається на нуль або не існує і,
проходячи через цю точку, похідна змінює
знак.
має екстремум, то її похідна в цій точці
обертається на нуль або не існує і,
проходячи через цю точку, похідна змінює
знак.
У випадку мінімуму похідна, проходячи через цю точку зліва направо, змінює знак з «-» на «+», у випадку максимуму – з «+» на «-».
Функція
![]() в точці
в точці
![]() має максимум (мінімум), якщо в цій точці
має максимум (мінімум), якщо в цій точці
![]() і
і
![]() .
.
Якщо в
точці
![]() перша похідна від функції обертається
на нуль, а перша відмінна від нуля похідна
буде парного
перша похідна від функції обертається
на нуль, а перша відмінна від нуля похідна
буде парного
порядку, то в цій точці функція має екстремум, при чому мінімум, якщо ця похідна додатна, і максимум, якщо від’ємна.
