3.2.2 Границя функції. Обчислення границь

Нехай функція визначена в деякому околі Х точки , крім, можливо, самої точки . Число А є границею функції в точці , якщо для довільного числа існує число таке, що для всіх , які задовольняють нерівність

,

виконується нерівність

.

Позначення:

.

Функція при є нескінченно великою (має границю ), якщо вона визначена в деякому околі точки, крім, можливо, самої точки , і для довільного числа існує таке , що для всіх , які задовольняють нерівність

,

виконується нерівність

.

Позначення:

.

Функція при є нескінченно великою (має границю ), якщо вона визначена в деякому околі точки , крім, можливо, самої точки , і для довільного числа існує таке , що для всіх , які задовольняють нерівність , виконується нерівність

.

При функція є нескінченно великою, якщо для довільного числа можна знайти таке число , що для всіх , які задовольняють нерівність , виконується нерівність .

Функція є нескінченно великою при (), якщо .

Деякі властивості нескінченно малих величин:

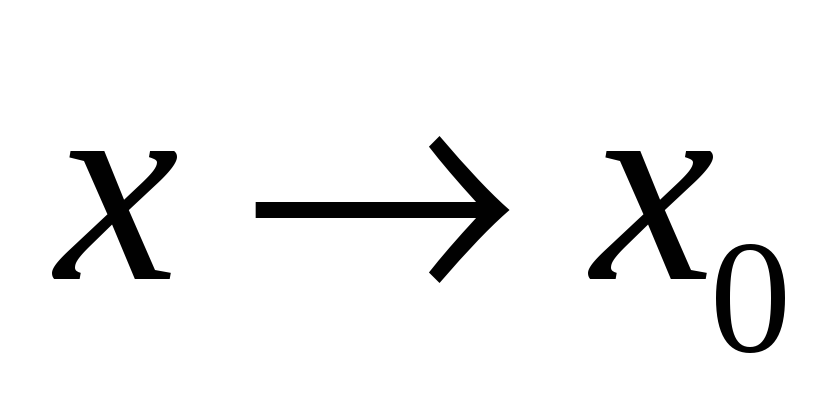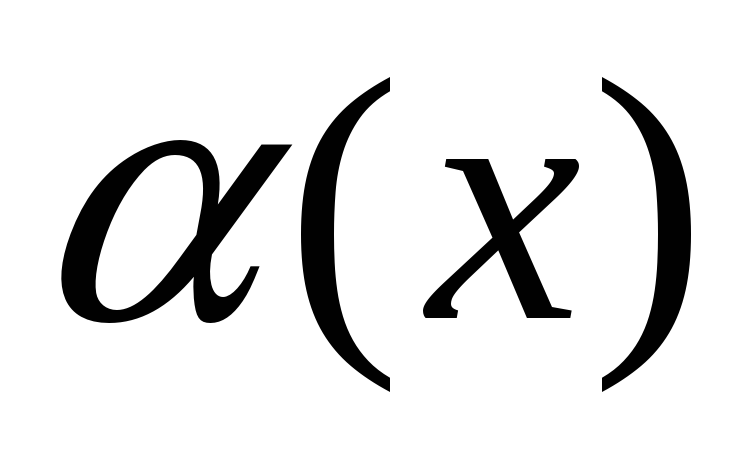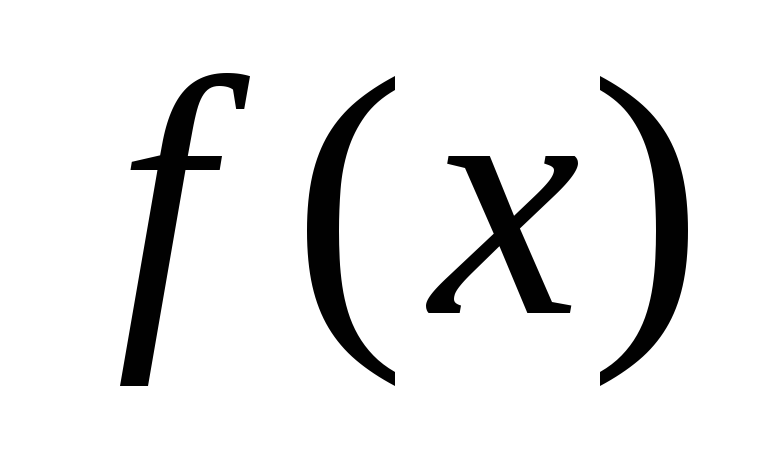1. якщо при () - нескінченно мала, а - нескінченно велика величина, то при 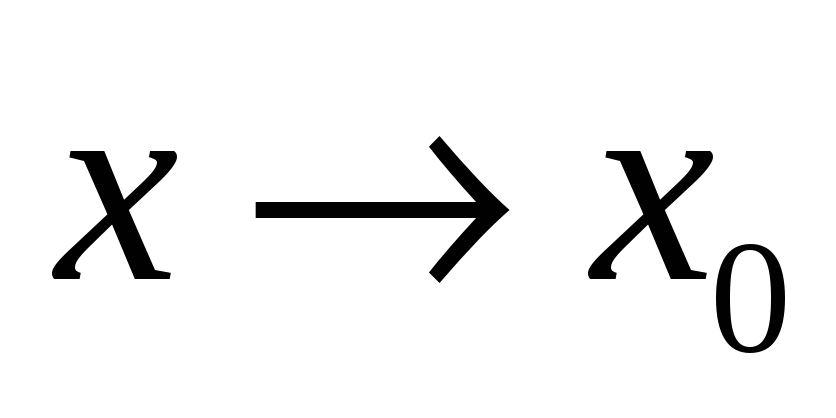() 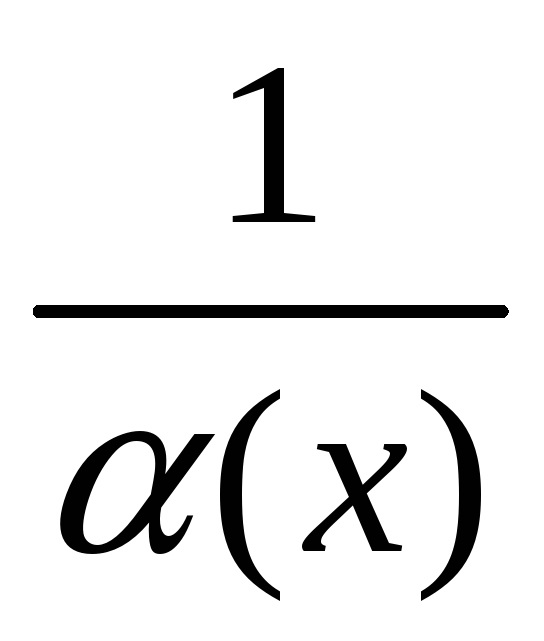і 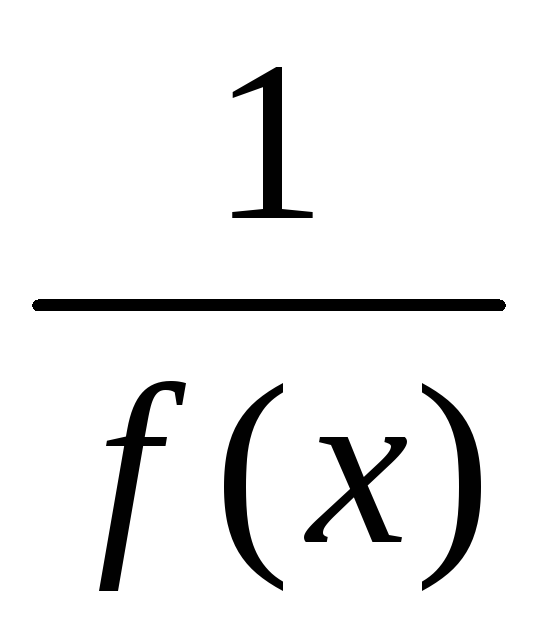- відповідно нескінченно велика і нескінченно мала велечини;

2. сума скінченого числа нескінченно малих величин є нескінченно малою величиною;

3. добуток обмеженої функції на нескінчену малу є нескінченно малою величиною;

4. частка від ділення нескінченно малої величини на функцію, яка має відміну від нуля границю, є нескінченно малою величиною.

Якщо кожна з функцій та має скінчену границю при (), то справедливі формули:

1)

2)

3)

4)

При обчисленні границь часто використовують такі границі:

- перша важлива границя;

- друга важлива границя.

Число є границею функції зліва(лівою границею) в точці

Число є границею функції справа(правою границею) в точці , якщо для будь-якого числа існує таке, що при виконується нерівність

Ліва і права границі функції називаються односторонніми границями.

3.2.3 Неперервність функції

Функція є неперервною в точці , якщо виконуються такі умови:

1. функція визначена в точці 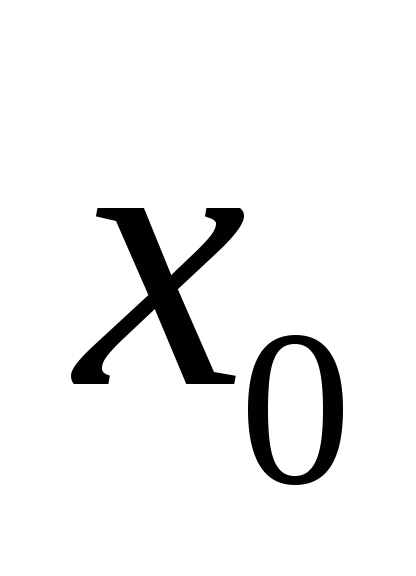і в деякому околі цієї точки;

2. існують скінчені односторонні границі функції 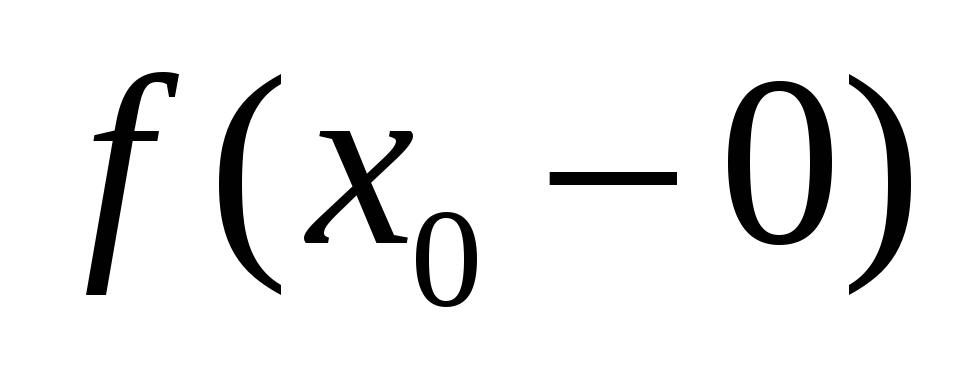і ;

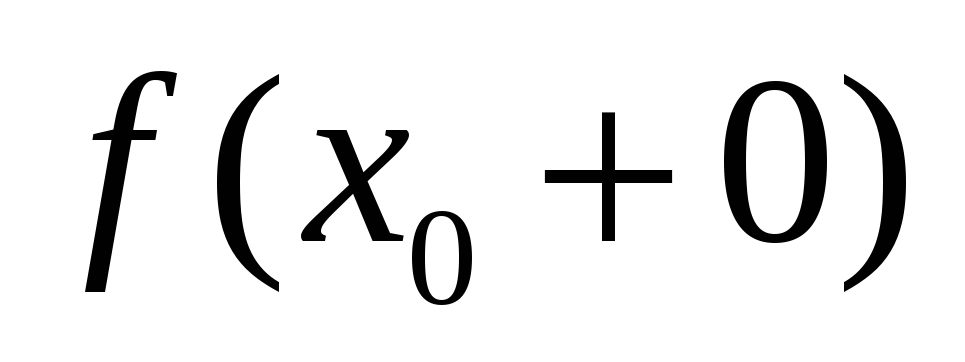3. односторонні границі рівні між собою і дорівнюють значенню функції в точці 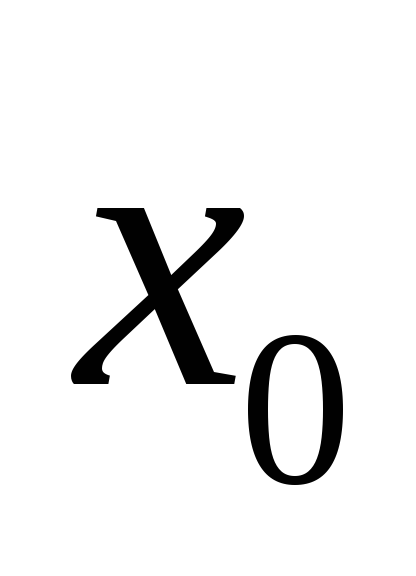, тобто .

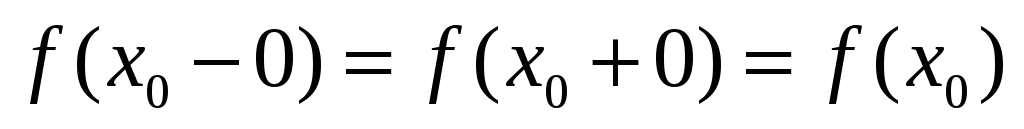Якщо не виконується хоча б одна з цих умов, то функція є розривною в точці , а сама точка - точкою

розриву функції.

Якщо функція визначена в точці й існують скінченні односторонні границі, але не всі числа рівні між собою, то розрив функції в точці є розривом першого роду, а точка

- точкою розриву першого роду. Величина є стрибком функції. Зокрема, якщо , то розрив у точці є усувним, а точка - точкою усувного розриву. Довизначивши функцію в точці рівністю , дістанемо непервну функцію.

Якщо хоча б одна із односторонніх границь не існує або дорівнює нескінченності, то розрив функції в точці є

розривом другого роду, а точка - точкою розриву другого роду.

Функція неперервна на відрізку , якщо вона непервна в кожній внутрішній точці цього вірізка, а також у точці справа і в точці зліва.

Всі елементарні функції неперевні в області свого визначення.

Якщо функція неперервна на відрізку , то:

1. вона обмежена на цьому відрізку і досягає на ньому принаймні один раз свого найбільшого і найменшого значення;

2. набуває всіх проміжних значень між найменшим і найбільшим значеннями;

2. при зміні знаку функції на відрізку знайдеться принаймні одна точка 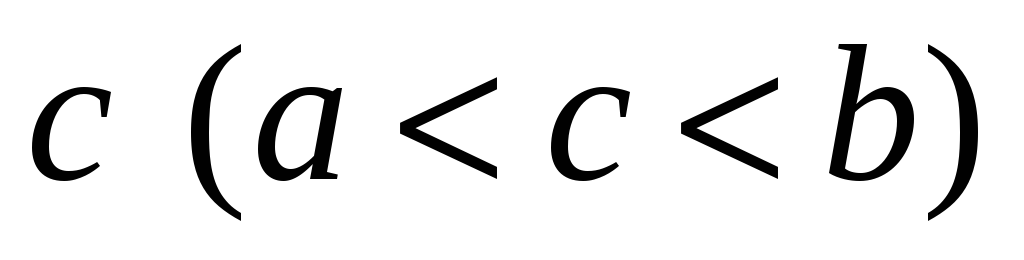, в якій .

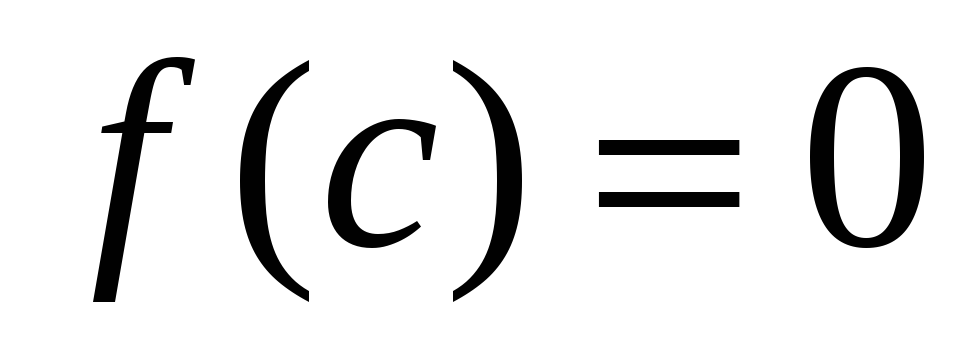I.Довести, що функція неперервна на всій числовій прямій

1. ;

2. ;

3. ;

4.

II. Дослідіть на неперервність наступні функції в точці :

1. в т. ;

2. в т. ;

3. в т. ;

4. в т. ;

5. в т. ;

6. в т. ;

7. в т. ;

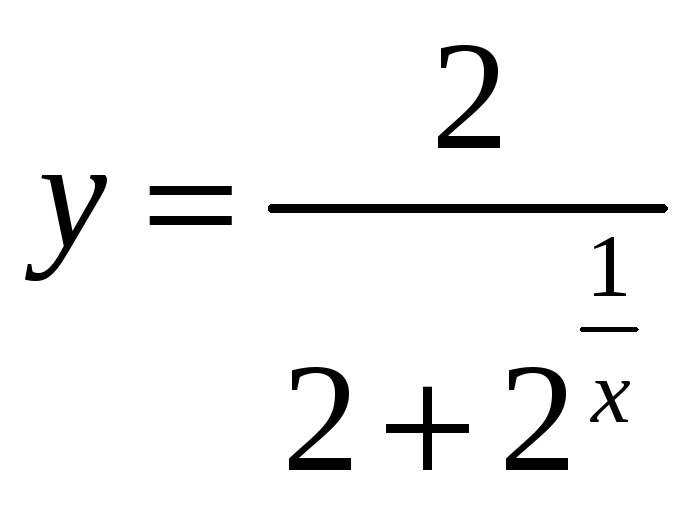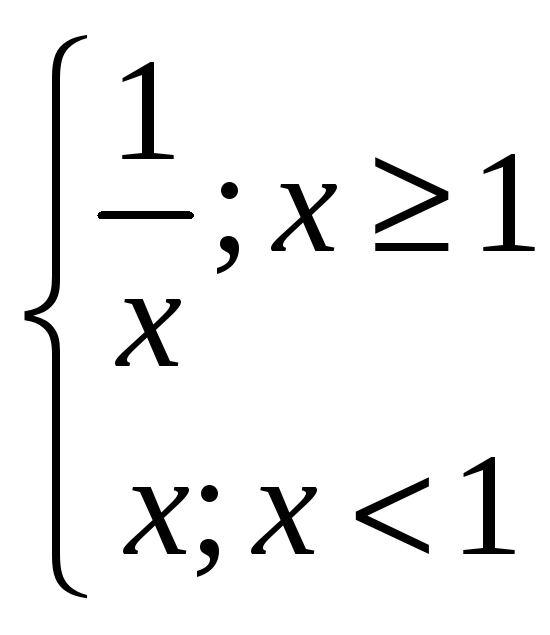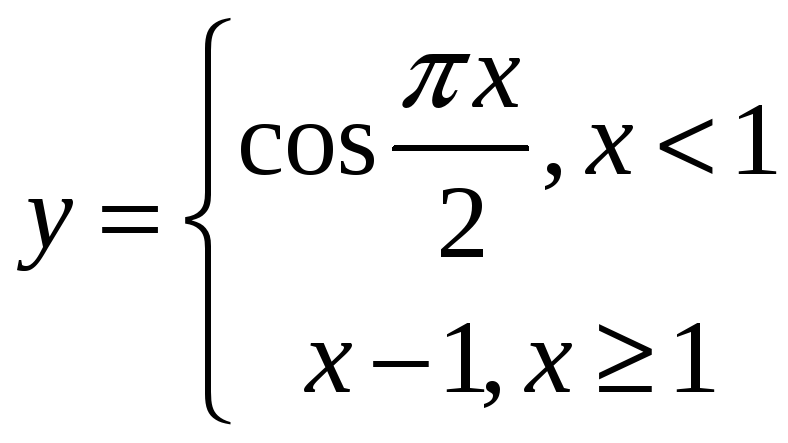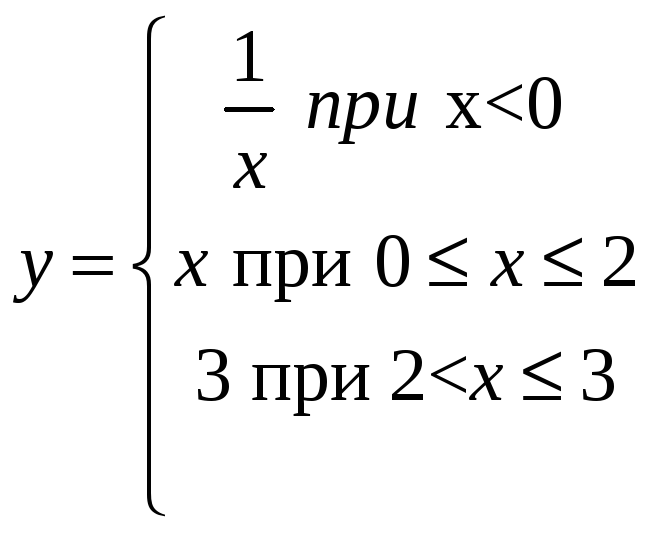8. в т. .

III. Обчислити границю:

1. ; 2. ;

3. ; 4. .

IV. Знайти область визначення функції:

1. ; 2. ;

3. ; 4. ;

5. ; 6. ;

7. ; 8. .

V. Які із функцій є парними, які непарними:

1. ; 2. .

VI. Обчислити границю:

1. ; 2. ;

3. ; 4. ;

5. ; 6. ;

7. ; 8. ;

9. ; 10. ;

11. ; 12. ;

13. ; 14. ;

15. ; 16. ;

17. ; 18. ;

19. ; 20. ;

21. ; 22.;

23. ; 24. .