
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§2. Предикаты.
Рассмотрим следующие высказывания.
-
… больше
 .
. -
∘∘∘∘
 ‒
‒ ‒ ‒
‒
‒ ‒ ‒
-
*** есть отец ~~~~
-
∙∙∙∙∙∙∙ + ‒‒‒‒‒<*****
Это предикаты, своего рода заготовки для предложений.
Определение.
Предикатом называется высказывание, содержащее одно или несколько пустых мест и обращающиеся в предложение всякий раз, когда пустые места (переменные) замещены конкретными предметами, принадлежащими некоторым определённым классам объектов.
Пустые места будем обозначать буквами x, y, z, …, а сами предикаты буквами P, Q, R, … .
P(x) – предикат, содержащий одно переменное.
Q(x, y) – предикат, содержащий две переменные (два пустых места).
Примеры предикатов.
-
x>

-
x

-
z отец υ
-
x+y<ω
Над предикатами можно производить такие же действия, как и над предложениями.
В то же время в отличи от предложений предикаты не могут быть ни истинными, ни ложными.
§3. Кванторы.
Замещение пустых мест в предикате не единственный способ получения предложений.
Пусть
P(x) x – певец мужского хора МИФИ.
x – певец мужского хора МИФИ.
Условимся замещать x – всеми мальчиками, присутствующими в аудитории на лекции.
Символ
 условимся читать как „каждый” или
„любой”, или „все”, а символ
условимся читать как „каждый” или
„любой”, или „все”, а символ
 - как „существует”, „найдётся” или
„есть хоть один”.
- как „существует”, „найдётся” или
„есть хоть один”.
Тогда
 P(x)
– все присутствующие поют в хоре МИФИ.
P(x)
– все присутствующие поют в хоре МИФИ.
 x:
P(x)
– среди присутствующих есть хоть один,
поющий в хоре МИФИ.
x:
P(x)
– среди присутствующих есть хоть один,
поющий в хоре МИФИ.
Определение.
Символы
 называются квантором
общности и
квантором
существования
соответственно.
называются квантором
общности и
квантором
существования
соответственно.
Q(x,
y)
 x прочитал y.
x прочитал y.
{y} – произведения де Сент-Экзюпери.
x – присутствующие в аудитории.
 x
x
 :
Q(x,
y)
(v)
:
Q(x,
y)
(v)

 :
Q(x,
y)
(vv)
:
Q(x,
y)
(vv)
В
математике в тех случаях, когда А
 В истинно, то говорят, что В является
необходимым
условием для А, а А – достаточным
условием для В.
В истинно, то говорят, что В является
необходимым
условием для А, а А – достаточным
условием для В.
При
построении отрицания предложения,
полученного воздействием кванторов на
предикат все
объекты остаются на своих местах,
каждый квантор
общности
 яется
на квантор существования
яется
на квантор существования
 ,
а каждый квантор
существования
,
а каждый квантор
существования
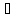 заменяется на квантор общности
заменяется на квантор общности
 и над предикатом ставится черта.
и над предикатом ставится черта.
Примеры.
-
(А)
 ({xn}
ограничена)
({xn}
ограничена)
 ({xn}
ограничена сверху)
({xn}
ограничена сверху) (
{xn}
ограничена снизу)
(
{xn}
ограничена снизу)
 (
( В
В
 n:
xn
n:
xn В)
В) (
( А
А
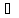 n:
А
n:
А xn)
xn)
( )
)
 ({xn}
неограниченна)
({xn}
неограниченна)
 ({xn}
неограниченна сверху)
({xn}
неограниченна сверху) ({xn}
неограниченно снизу)
({xn}
неограниченно снизу)
 (
( В
В
 n:
xn>В)
n:
xn>В) (
( А
А
 n:
А>xn)
n:
А>xn)
-
(В)
 ({xn}
монотонна)
({xn}
монотонна)
 ({xn}
убывает)
({xn}
убывает) ({xn}
возрастает)
({xn}
возрастает)
 (
( :
xn
:
xn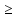 xn+1)
xn+1) (
( :
xn
:
xn xn+1)
xn+1)
( )
)
 ({xn}
не является монотонной)
({xn}
не является монотонной)
 ({xn}
неубывающая)
({xn}
неубывающая) ({xn}
невозрастающая)
({xn}
невозрастающая)
 (
( :
xń<xń+1)
:
xń<xń+1) (
( ň:
xň>xň+1)
ň:
xň>xň+1)
-
(С)
 ({xn}
сходится)
({xn}
сходится)
 (
(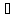 а:
а=
а:
а= xn)
xn)
 (
( а
а
 >0
>0
 N
N
 n>N:
│xn
- а│<
n>N:
│xn
- а│< )
)
( )
)
 ({xn}
расходится)
({xn}
расходится)
 (
( а
а
 >0
>0
 N
N
 n:
│xn
- а│
n:
│xn
- а│ )++++++++
)++++++++
-
(D)
 ({xn}
б.м.)
({xn}
б.м.)
 (0=
(0= xn)
xn)
 (
( >0
>0
 N
N
 :
│xn│<
:
│xn│< )
)
( )
)
 ({xn}
не является б.м.)
({xn}
не является б.м.)
 (
( >0
>0
 N
N
 :
│xn│
:
│xn│ )
)
§4. Предельный переход в неравенствах. (Глава 2)
Теорема 1. (Для одной последовательности).
Пусть {xn}
сходится и
 xn=а,
и пусть
xn=а,
и пусть
 В
такое, что
В
такое, что
 n,
n=1, 2, … : xn
n,
n=1, 2, … : xn В
(
В
( А
А
 :
xn
:
xn А).
А).
Тогда
а В
(соответственно, А
В
(соответственно, А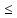 а).
а).
Доказательство.
-
Рассмотрим произвольную последовательность {xn}, а=
 xn
и пусть
xn
и пусть
 В
В
 n,
n=1, 2, … : xn
n,
n=1, 2, … : xn В.
В.
Предположим противное: а>В.
Так как
 xn=а
xn=а

 >0,
а значит и для
>0,
а значит и для
 =а-В>0,
=а-В>0,
 N
N
 n>N:
│xn
- а│<а-В
n>N:
│xn
- а│<а-В
 -а+В+а<xn<а-В+а
-а+В+а<xn<а-В+а
 В<xn<2а-В
В<xn<2а-В
Мы
пришли к противоречию с тем, что
 :
xn
:
xn В.
В.
-
Рассмотрим произвольную последовательность {xn}, а=
 xn,
для которой существует А такое, что
xn,
для которой существует А такое, что
 :
xn
:
xn А
А
 -xn
-xn -А
-А
Тогда для
последовательности {-xn}
выполняется
 (-xn)=
-а и для каждого n, n=1, 2, … : -xn
(-xn)=
-а и для каждого n, n=1, 2, … : -xn -А.
Согласно п. I
-а
-А.
Согласно п. I
-а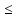 -А
-А

 .
.
Замечание.
Если
в условиях теоремы 1 неравенство строгое,
то в утверждении теоремы 1 следует
сохранить
нестрогие неравенства а В
(соответственно, а
В
(соответственно, а А).
А).
Пример.
{xn}={ }.
}.
 n:
n:
 >0
>0
Но
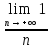 =0.
=0.
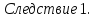
Пусть {xn}
такова, что
 :
А
:
А xn
xn В
и
В
и
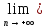 xn=а.
xn=а.
Тогда А а
а В.
В.
Указанное свойство отрезка [А, В] называется свойством замкнутости, то есть если на отрезке располагается сходящаяся последовательность, то отрезок не выпустит за свои границы предел этой последовательности.
Интервал (А, В) таким свойством не обладает.
Следствие 2.
Если
последовательности {xn}
и {yn}
сходятся, причём
 xn=а,
xn=а,
 yn=b
и
yn=b
и
 ,
n=1, 2, …: xn
,
n=1, 2, …: xn yn,
то а
yn,
то а b.
b.
Доказательство.
Рассмотрим
{yn-xn}.
 :
yn-xn
:
yn-xn 0.
Согласно теореме 3 §2
0.
Согласно теореме 3 §2
 (yn-xn)=b-а,
а согласно теореме 1 §4 b-а
(yn-xn)=b-а,
а согласно теореме 1 §4 b-а 0
0
 а
а b.
b.
Теорема 2. (о трёх последовательностях)
Пусть
{xn},
{yn}
и {zn}
таковы, что: 1)
 :
xn
:
xn zn
zn yn
yn
2)
 xn=
xn= yn=а
yn=а
Тогда {zn}
сходится и
 zn=а.
zn=а.
Доказательство.
 xn=а
xn=а

 0
0
 N1
N1
 >N1:
│xn
- а│<
>N1:
│xn
- а│<
 а-
а- <xn<а+
<xn<а+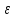
 yn=а
yn=а

 >0
>0
 N2
N2
 >N2:
│yn
- а│<
>N2:
│yn
- а│<
 а-
а- yn<а+
yn<а+
Возьмём
произвольной
 0
и положим N=max{N1,
N2}.
0
и положим N=max{N1,
N2}.
Тогда
 >N:
>N:


 >N:
а-
>N:
а-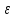 <xn
<xn zn
zn yn<а+
yn<а+
 а-
а- <
zn<а+
<
zn<а+
Следовательно,


 >N:
│zn
- а│<
>N:
│zn
- а│<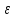

 zn
=а.
zn
=а.
