
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§3. Свойства сходящихся последовательностей.
Теорема 1.
Любая сходящаяся последовательность имеет единственный предел.
Доказательство. (от противного)
Пусть существует {xn}, такая сходящаяся последовательность, для которой существуют два числа а и b, а<b , такие что
а=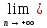 xn,
b=
xn,
b= xn,
b>a.
xn,
b>a.
так как a<b, то существуют непересекающиеся окрестности точек а и b.

Возьмём
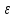 =
=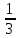 (b-а)>0.
(b-а)>0.
а= xn
xn
 для каждого
для каждого
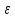 >0,
а значит и для
>0,
а значит и для
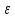 =
= (b-а)>0
существует номер N1
такой, что для любого n> N1:
│ xn-а│<
(b-а)>0
существует номер N1
такой, что для любого n> N1:
│ xn-а│< (b-а).
(b-а).
b= xn
xn
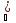 для каждого
для каждого
 >0,
а значит и для
>0,
а значит и для
 =
= (b-а)>0
существует номер N2
такой, что для любого номера n>N2:
│xn-b│<
(b-а)>0
существует номер N2
такой, что для любого номера n>N2:
│xn-b│<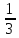 (b-а).
(b-а).
Тогда для любого n>N=max{N1, N2} выполняются оба неравенства:





 b-
b- xn<a+
xn<a+
 b-
b- a+
a+
 b-a<2
b-a<2 =
= (b-а),
что невозможно.
(b-а),
что невозможно.
Мы пришли к противоречию.
Теорема 2.
Любая сходящаяся последовательность ограничена. Обратное неверно.
Доказательство.
I. Пусть {xn} сходится. Докажем, что она ограничена.
{xn}
сходится
 существует число а
существует число а такое, что для каждого
такое, что для каждого
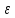 >0,
а значит и для
>0,
а значит и для
 =1>0
существует номер N=N(1) такой, что для
любого номера n>N:
=1>0
существует номер N=N(1) такой, что для
любого номера n>N:
│ xn-а│< =1
=1
 а-1< xn<а+1
а-1< xn<а+1
 xn
xn (а-1,
а+1)
(а-1,
а+1)

Положим А=min{x1, x2, …, xN, a-1}
B=max{ x1, x2, …, xN, a+1}
Тогда для
любого n, n=1, 2, …: А В.
В.
II. Обратное неверно.
Рассмотрим последовательность 0, 1, 0, 1, …
Она ограничена числами 0 и 1.
Докажем,
что она расходится.
Для этого заметим, что если {xn}
сходится, то
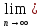 (xn+1-
xn)=0.
Действительно, возьмём произвольное
(xn+1-
xn)=0.
Действительно, возьмём произвольное
 >0
и зафиксируем его.
>0
и зафиксируем его.
{xn}
сходится
 существует а такое, что для каждого
существует а такое, что для каждого
 >0,
а значит и для нашего фиксированного
>0,
а значит и для нашего фиксированного
 >0
существует номер N такой, что для любого
номера
>0
существует номер N такой, что для любого
номера
n>N: │xn-а│<
 а-
а- <
xn<а+
<
xn<а+
n+1>N:
│xn+1-а│<
 а-
а- <
xn+1<а+
<
xn+1<а+
Тогда │xn+1-
xn│=│xn+1-а-
xn+а│< =
=

 (xn+1-
xn)=0.
(xn+1-
xn)=0.
Вернёмся теперь к последовательности 0, 1, 0, 1, …
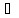 n, n=1, 2, …: │xn+1-
xn│=1
n, n=1, 2, …: │xn+1-
xn│=1
 0, следовательно {xn}
расходится.
0, следовательно {xn}
расходится.
Арифметические свойства сходящихся последовательностей.
Теорема 3.
Пусть {xn} и {yn} две сходящиеся последовательности.
 xn=а,
xn=а,
 yn=b.
yn=b.
Тогда {xn+ yn } сходится и её предел равен а+b.
Доказательство.
 xn=а
xn=а
 для любого n: xn=а+
для любого n: xn=а+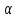 n,
где {
n,
где {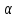 n}
- б.м.
n}
- б.м.
 yn=b
yn=b
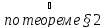 для любого n: yn=b+
для любого n: yn=b+ n,
где {
n,
где {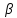 n}
– б.м.
n}
– б.м.
Тогда {xn+yn
} сходится, т.к.
 n, n=1, 2, …:
xn+yn=(а+
n, n=1, 2, …:
xn+yn=(а+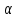 n)+(b+
n)+(b+ n)=а+b+(
n)=а+b+( n+
n+ n),
n),
{ n+
n+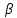 n
} – б.м., как сумма двух бесконечно малых
последовательностей {
n
} – б.м., как сумма двух бесконечно малых
последовательностей { n}
и{
n}
и{ n}.
n}.
Согласно
лемме 2 §2
 (xn+yn)=а+b
(xn+yn)=а+b
Теорема 4.
Пусть {xn}
и {yn}
две сходящиеся последовательности,
 xn=а,
xn=а,
 yn=b.
yn=b.
Тогда {xnyn} сходится и её предел равен а∙b.
Доказательство.
 xn=а
xn=а
 для каждого n: xn=а+
для каждого n: xn=а+ n,
где {
n,
где { n}
– б.м.
n}
– б.м.
 yn=b
yn=b
 для любого n: yn=b+
для любого n: yn=b+ n,
где {
n,
где { n}
– б.м.
n}
– б.м.
Тогда для любого n:
xn
yn=(а+ n)∙(b+
n)∙(b+ n)=аb+а
n)=аb+а n+b
n+b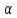 n+
n+ n
n n
n
Последовательности
{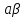 n}
и {
n}
и { n}
бесконечно малые по лемме 1 §2, {
n}
бесконечно малые по лемме 1 §2, { n
n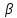 n}
– б.м., как произведение ограниченной
на бесконечно малую
n}
– б.м., как произведение ограниченной
на бесконечно малую
 по теореме 1§2
по теореме 1§2
 xnyn=а∙b.
xnyn=а∙b.
Теорема 5.
Пусть {xn}
и {yn}
две сходящиеся последовательности,
 xn=а,
xn=а,
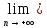 yn=b,
b
yn=b,
b 0.
0.
Тогда { }
сходится и её предел равен
}
сходится и её предел равен
 .
.
Доказательство.
I.
Пусть
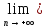 yn=b,
b
yn=b,
b .
.
Тогда
последовательность { }:
1) имеет смысл
}:
1) имеет смысл
2) сходится
3) её предел равен

1) {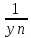 }
имеет смысл, то есть существует
номер nо такой, что для любого n
}
имеет смысл, то есть существует
номер nо такой, что для любого n о:
yn
о:
yn ,
то есть {
,
то есть { }
} определена.
определена.
В самом деле,
т.к.
 yn=b
yn=b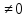
 для каждого
для каждого
 0,
а значит и для
0,
а значит и для
 >0,
существует номер N такой, что для любого
номера n>N
>0,
существует номер N такой, что для любого
номера n>N
│yn-b│<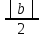
 b-
b- <yn<b+
<yn<b+
Пусть
b>0.
 │b│=b.
│b│=b.
Тогда
0<b-
 ∙b=
∙b= <yn<
<yn< ∙b
(*)
∙b
(*)
Пусть
b<0.
 │b│= - b.
│b│= - b.
Тогда
 ∙b<
yn<
∙b<
yn< ∙b<0
(**).
∙b<0
(**).
Тогда для
любого n N+1:
yn
N+1:
yn и {
и { }
} опеределена.
опеределена.
2) Покажем,
что { }
ограничена.
}
ограничена.
Для любого
n>N: либо 0< <yn
<yn
 │
│ │<
│< ,
,
либо yn<
 <0
<0
 │
│ │<
│<
 {
{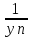 }
} ограничена.
ограничена.
3) Докажем,
что {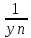 }
сходится и её предел равен
}
сходится и её предел равен
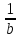 .
.
Так как
 yn=b
yn=b
 для любого n: yn=b+
для любого n: yn=b+ n,
где {
n,
где {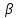 n}
– б.м.
n}
– б.м.
Пусть n о:
о:
 =
=
 =
=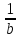 (b - yn)
=
(b - yn)
=
 n
.
n
.
{ n
} по лемме 3 §2 б.м., ибо {b-
yn
}={-
n
} по лемме 3 §2 б.м., ибо {b-
yn
}={- n
} – б.м.
n
} – б.м.
А тогда
 =
=
 +
+ -
-
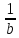 =
=
 +
+ n
, {
n
, { n
} б.м. и согласно теореме 1§2,
n
} б.м. и согласно теореме 1§2,
 =
=
 .
.
II.
Докажем теперь, что{xn∙ }=
{
}=
{ }
сходится.
}
сходится.
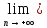 xn=а,
xn=а,
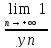 =
=
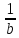 .
.
Тогда
по теореме 3 { }
сходится и её предел равен
}
сходится и её предел равен
 .
.
Теорема 6.
Пусть {xn}
сходится и
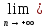 xn=а.
xn=а.
Тогда {│xn│}
сходится и
 │xn│=│а│.
│xn│=│а│.
Доказательство.
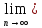 xn=а
xn=а
 для каждого
для каждого
 >0
существует номер N такой, что для любого
номера n>N: │xn
- а│<
>0
существует номер N такой, что для любого
номера n>N: │xn
- а│< .
.
Возьмём
произвольное
 >0,
фиксируем его. Тогда
>0,
фиксируем его. Тогда
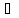 n>N: ││xn│
- │а││
n>N: ││xn│
- │а││ │xn
- а│<
│xn
- а│<

 │xn│=│а│.
│xn│=│а│.
