
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
Глава 6. Дифференцируемая функция. Дифференциал.
§1. Понятие дифференцируемой функции в точке и дифференциала.
Определение.
Пусть f(x) имеет стандартную область определения X, xо – внутренняя точка одного из промежутков, образующих X.
Функция f(x)
называется дифференцируемой в точке
xо, если её приращение в точке
xо ∆f(xо; ∆x), вызванное
смещением ∆x, может быть представлено
в виде ∆f(xо; ∆x)=A·∆x+ (∆x),
где A –число, а
(∆x),
где A –число, а
 (∆x)=
(∆x)= .
.
Определение.
Пусть f(x) дифференцируема в точке xо. Главная линейная часть приращения функции называется дифференциалом функции f(x) в точке xо.
Обозначение:


∆f(xо;
∆x)=A·∆x+ (∆x)=df+
(∆x)=df+ ,
то есть
,
то есть
 =0
=0
Примеры.
-
f(x)=
 ,
X=(
,
X=( ,
+
,
+ )
)
xо=2
∆f(2; ∆x)= =
=4+4∆x+
=4∆x+
A=4,
 (∆x)=
(∆x)= =
=
df=4∆x
-
f(x)=
 ,
X=(
,
X=( ,
+
,
+ )
)
а) xо=8
 ∆f=∆f(8; ∆x)=f(8+∆x)
∆f=∆f(8; ∆x)=f(8+∆x) f(8)=
f(8)= =
=
 1
1 ∆x
∆x
Главная линейная часть
 в точке xо =8.
в точке xо =8.
∆f(8; ∆x)= ∆x+
∆x+
б) xо =7. ∆f(7; ∆x)= ∆f(7;
∆x) f(7)=
f(7)= =
= .
.
Главной частью приращения функции
∆f является
 ,
A=0,
,
A=0,
 0.
0.
Функция f(x)= не является дифференцируемой в точке
xо=7, так как приращение функции
не является линейной от ∆x при
не является дифференцируемой в точке
xо=7, так как приращение функции
не является линейной от ∆x при

(∆f(7; ∆x)= имеет порядок
имеет порядок
 при
при
 )
)
Теорема 1. (Необходимое условие дифференцируемости функции в точке.)
Пусть f(x) имеет стандартную область определения X, и во внутренней точке xо одного из промежутков X f(x) дифференцируема.
Тогда f(x) непрерывна в точке xо.
Доказательство.
f(x) дифференцируема
в точке xо X.
Сместимся из точки xо в точку
xо+∆x
X.
Сместимся из точки xо в точку
xо+∆x X.
X.
Тогда ∆f(xо;
∆x)=f(xо+∆x) f(xо)=
A·∆x+
f(xо)=
A·∆x+

 ∆f(xо; ∆x)=
∆f(xо; ∆x)= (A·∆x+
(A·∆x+ )=0.
)=0.
f(x) непрерывна в точке xо.
Теорема 2. (Необходимое и достаточное условие дифференцируемости функции в точке).
Пусть f(x) имеет стандартную область определения X, xо – внутренняя точка одного из промежутков из X.
f(x) дифференцируема
в точке xо тогда и только тогда,
когда
 f´(xо).
f´(xо).
Доказательство.
-
Необходимость.
xо X,
xо+∆x
X,
xо+∆x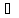 X,
∆x
X,
∆x 0.
0.
f(x) дифференцируема в точке xо
 ∆f(xо; ∆x)= A·∆x+
∆f(xо; ∆x)= A·∆x+ (∆x),
A-число,
(∆x),
A-число,
 (∆x)=
(∆x)= .
.
Тогда
 f´(xо)=
f´(xо)= =
= =
= =A.
=A.

-
Достаточность.
Пусть во внутренней точке xо X
X
 f´(xо).
f´(xо).
Докажем, что f(x) дифференцируема в точке xо.
Так как
 f´(xо)=
f´(xо)=

 =f´(xо)+
=f´(xо)+ (∆x),
где
(∆x),
где
 (∆x)=0
(∆x)=0
 ∆f(xо; ∆x)= f´(xо)∆x+
∆f(xо; ∆x)= f´(xо)∆x+ (∆x)·∆x.
Положим A= f´(xо),
(∆x)·∆x.
Положим A= f´(xо),
 (∆x)=
(∆x)= (∆x)·∆x.
(∆x)·∆x.
Тогда
 =
= =
= (∆x)=0
(∆x)=0

 (∆x)=
(∆x)=

f(x) дифференцируема в точке xо и
df= f´(xо)∆x
 ∆f(xо; ∆x)= f´(xо) ∆x+
∆f(xо; ∆x)= f´(xо) ∆x+ (∆x),
(∆x),
 (∆x)=
(∆x)= .
.
Следствие 1.
Рассмотрим функцию
 (x)=x
(x)=x
 ∆
∆ =∆x,
=∆x,
 (∆x)=0
(∆x)=0
 d
d =dx=
∆x
=dx=
∆x
 Дифференциал независимой переменной
есть её приращение
Дифференциал независимой переменной
есть её приращение
 то есть dx не зависит от x!!!
то есть dx не зависит от x!!!
А тогда df= f´(x)·dx.
Следствие 2.
Если в точке существует дифференциал,
то он единственен, так как
 единственное значение производной
функции в точке, ибо предел функции
единственен.
единственное значение производной
функции в точке, ибо предел функции
единственен.
Следствие 3.
Пусть в точке x X
X
 f´(x).
f´(x).
-
f´(x)
 0.
0.
Тогда ∆f= ∆f(x; ∆x)=f´(x)·dx+ (∆x)=df+
(∆x)=df+


-
f´(x)=0
 df= f´(x)·dx=0
df= f´(x)·dx=0

§2. Некоторые свойства дифференциала функции в точке.
Из свойств производных следует:
-
dv=dC=0.
Дифференциал постоянной равен 0.
v(x) C
на (
C
на ( ,
+
,
+ ).
).
-
d(C·u(x))=C·du(x)/
Константа выносится за знак дифференциала.
-
d(u + v)=du+dv
-
d(u· v)=du· v+u·dv
-
d
 =
=

