
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
Пусть f(x) задана на промежутке X ненулевой длины и монотонна на X.
Теорема 1.(О существовании односторонних пределов функции во внутренних точках промежутка.)
Пусть функция f(x) монотонна на промежутке X ненулевой длины. Тогда в любой внутренней точке промежутка X функция f(x) имеет односторонние пределы.
Доказательство.
а) Пусть f(x)
возрастает на X

 x´,
x´´
x´,
x´´ X
(x´< x´´): f(x´)
X
(x´< x´´): f(x´) f(x´´)
и пусть xо – внутренняя точка
промежутка X.
f(x´´)
и пусть xо – внутренняя точка
промежутка X.
Рассмотрим множества
X1={x;
x X:
x< xо}; Y1={f(x),
x
X:
x< xо}; Y1={f(x),
x X1}
X1}
X2={x;
x X:
x> xо};
Y2={f(x),
x
X:
x> xо};
Y2={f(x),
x X2}
X2}
Множество
Y1 ограничено сверху,
так как
 x
x X1:
f(x)
X1:
f(x)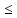 f(xо)
и, следовательно, Y1
имеет точную верхнюю грань L1=
supX1
f(x)= sup
Y1.
f(xо)
и, следовательно, Y1
имеет точную верхнюю грань L1=
supX1
f(x)= sup
Y1.
А множество
Y2 ограничено снизу,
так как
 x
x X2:
f(xо)
X2:
f(xо) f(x)
и L2= infX2
f(x)= inf
Y2.
f(x)
и L2= infX2
f(x)= inf
Y2.
Так как f(xо)
является одной из верхних границ
множества Y1 и одной
из нижних границ множества Y2,
то L1 f(xо)
f(xо) L2.
L2.
Докажем, что
-
L1=
 f(x)
f(x) -
L2=
 f(x)
f(x)
Возьмём
произвольное
 >0
и зафиксируем его.
>0
и зафиксируем его.
-
Так как L1= supX1 f(x)
 1)
1)
 x
x X1:
f(x)
X1:
f(x)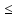 L1
L1
2)
 >0,
а значит и для нашего фиксированного
>0,
а значит и для нашего фиксированного
 >0
>0
 X1:
f(
X1:
f(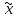 )>
L1–
)>
L1– .
.
 L1 –
L1 – <2)f(
<2)f( )
) 1)
L1< L1+
1)
L1< L1+ .
.
Тогда
 x
x X1,
X1,
 <x<
xо (x
<x<
xо (x (
( ,
xо)) в силу возрастания функции
f(x) на X:
f(
,
xо)) в силу возрастания функции
f(x) на X:
f( )
)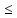 f(x)
f(x) L1
L1 f(xо)
f(xо)

 x
x X
X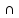 (
( ,
xо): L1–
,
xо): L1– <f(
<f( )
) f(x)
f(x) L1<
L1+
L1<
L1+ .
.
Положим
 1=
1=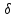 1(
1( )=
xо –
)=
xо – >0
(ибо
>0
(ибо
 =
= (
( )).
)).
Тогда
 >0
>0
 1>0
1>0
 x
(x
x
(x X1,
x< xо, │x -
хо│<
X1,
x< xо, │x -
хо│< 1):
│f(x) –L1│<
1):
│f(x) –L1│<

 f(x)=L1.
f(x)=L1.
-
Так как L2= infX2 f(x)
 1)
1)
 x
x X2:
L2
X2:
L2 f(x)
f(x)
 >0,
а значит и для нашего фиксированного
>0,
а значит и для нашего фиксированного
 >0
>0
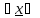 X2:
f(
X2:
f( )<
L2+
)<
L2+
 L2–
L2–
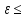 1)
L2<f(
1)
L2<f( )<2)
L2+
)<2)
L2+
 А тогда в силу возрастания функции f(x)
на X
А тогда в силу возрастания функции f(x)
на X
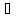 x
x X2,
xо<x<
X2,
xо<x< (x
(x (xо,
(xо,
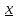 (
( ))
))
L2– <L2
<L2 1)
f(x)
1)
f(x) f(
f(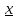 )<2)
L2+
)<2)
L2+ .
.
Положим
 2=
2= 2(
2( )=
)= (
( )
–xо>0.
)
–xо>0.
Тогда
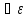 >0
>0
 2>0
2>0
 x
(x
x
(x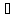 X2,
x>xо, │x -
хо│<
X2,
x>xо, │x -
хо│<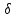 2):
L2–
2):
L2– <f(x)<
L2+
<f(x)<
L2+
 │f(x) –L2│<
│f(x) –L2│<
 L2=
L2= f(x).
f(x).
б)
Пусть f(x)
убывает на X. Рассмотрим функцию –f(x).
Она возрастает на X. Тогда по доказанному
в п.а) у неё есть односторонние пределы
в любой внутренней точке промежутка X,
а функция f(x)
отличается от –f(x)
только постоянным множителем (–1)
 f(x) имеет
односторонние пределы в каждой внутренней
точке промежутка.
f(x) имеет
односторонние пределы в каждой внутренней
точке промежутка.
Теорема 2. (Достаточные условия непрерывности строго монотонной функции.)
Пусть f(x)
определена на промежутке X. Строго
монотонна на X и Y={y;
y=f(x),
x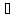 X}
- промежуток.
X}
- промежуток.
Тогда f(x) непрерывна на X.
Доказательство.
Для
определённости будем считать, чтоf(x)
строго возрастает на X, то есть
 x1,
x2
x1,
x2 X,
x1<x2: f(x1)<
f(x2).
X,
x1<x2: f(x1)<
f(x2).
Докажем, что f(x) непрерывна на X.
Предположим
противное, то есть что
 xо
xо X
такое, что f(x)
терпит разрыв в точке xо. По теореме
1, точка разрыва xо является точкой
разрыва 1-го рода.
X
такое, что f(x)
терпит разрыв в точке xо. По теореме
1, точка разрыва xо является точкой
разрыва 1-го рода.
xо X
X
 f(x)=L1=
supX1f(x)
f(x)=L1=
supX1f(x)
 f(x)=L2=
infX2
f(x) и L1
f(x)=L2=
infX2
f(x) и L1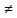 L2.
L2.
Но
так как L1 f(xо)
f(xо) L2, то предполагается, что
L2, то предполагается, что
-
L1< f(xо).
Возьмём точку x1 X1.
Тогда y1= f(x1)
X1.
Тогда y1= f(x1) L1< f(xо). y1= f(x1)<yо=
f(xо)
L1< f(xо). y1= f(x1)<yо=
f(xо)
 (y1, yо)
(y1, yо) Y={y;
y=f(x),
x
Y={y;
y=f(x),
x X}.
X}.
Возьмём произвольную точку y (y1,
yо) и L1<y<f(xо)=
yо.
(y1,
yо) и L1<y<f(xо)=
yо.
В самом деле, f(x)
строго возрастает
 x
x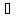 X1:
f(x)
X1:
f(x) L1<y
L1<y
 x
x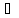 X2:
f(x)> f(xо)=
yо>y.
X2:
f(x)> f(xо)=
yо>y.
Но это
невозможно, так как Y={f(x),
x X}
– промежуток
X}
– промежуток
 L1=f(xо).
L1=f(xо).
-
Пусть f(xо)< L2=
 f(x)=
infX2
f(x).
f(x)=
infX2
f(x).
Возьмём некоторое x2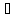 X2={x;
x>хо}
X2={x;
x>хо}
y2=f(x2) Y
Y
 весь интервал (yо, y2)
весь интервал (yо, y2) Y.
Y.
Рассмотрим точку y (yо,
y2) и f(xо)<y<L2.
(yо,
y2) и f(xо)<y<L2.
Проверим, что
 x
x X:
f(x)
X:
f(x)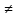 y.
В самом деле,
y.
В самом деле,
 x
x X1:
f(x)< f(xо)<y.
X1:
f(x)< f(xо)<y.
 x
x X2:
f(xо)<y<L2
X2:
f(xо)<y<L2 f(x)
.
f(x)
.
Но это невозможно, так как Y промежуток.
А тогда f(xо)= L2.
И мы получаем
L1= f(xо)=L2

 f(x)=
f(xо)=
f(x)=
f(xо)= f(x)
f(x)


 f(x)=
f(xо).
f(x)=
f(xо).
хо X
и
X
и
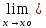 f(x)=
f(xо).
f(x)=
f(xо).
Следствие (теоремы 1).
Если функция монотонна на промежутке, и она имеет точки разрыва, то все они точки разрыва 1-го рода.
Следствие (теоремы о промежуточных значениях непрерывной функции и теоремы 2.)
(Критерий непрерывности строго монотонной функции.)
Строго
монотонная функция на промежутке X
ненулевой длины (в частности, на отрезке
[a, b], a<b)
является непрерывной на X тогда и только
тогда, когда её область значений Y={f(x),
x X}
является промежутком.
X}
является промежутком.
Определение.
Пусть f(x)
определена на промежутке X ненулевой
длины. Y={f(x),
x X}
– её область значений.
X}
– её область значений.
Функция f(x)
называется однозначно обратной на
X, если
 y
y Y
Y
 единственное x
единственное x X
такое, что y=f(x).
X
такое, что y=f(x).
Определение.
Пусть y=f(x)
однозначно обратима на X, Y={f(x),
x X}
– её область значений.
X}
– её область значений.
Функция
x=g(y) называется обратной к функции
y=f(x), если
она определена на Y, и каждому y Y
она ставит в соответствие именно то
единственной x
Y
она ставит в соответствие именно то
единственной x X,
для которого y=f(x).
X,
для которого y=f(x).
Обозначение
обратной функции: g(y)= f-1(y),
y Y.
Y.
Теорема 3.
Любая строго монотонная функция на промежутке X ненулевой длины однозначно обратима на нём.
Доказательство.
Пусть f(x)
строго возрастает на промежутке X,
Y={f(x), x X}.
X}.
f(x)
строго возрастает на X

 x1,
x2
x1,
x2 X,
x1<x2: f(x1)<
f(x2).
X,
x1<x2: f(x1)<
f(x2).
Возьмём
произвольное y Y,
зафиксируем его и покажем, что
Y,
зафиксируем его и покажем, что
 единственное x
единственное x X
такое, что y=f(x).
X
такое, что y=f(x).
Предположим,
что это не так, то есть
 x1,
x2
x1,
x2 X,
x1
X,
x1 x2
и такие, что y=f(x1)
и y=f(x2).
И мы сразу пришли к противоречию,
поскольку x1
x2
и такие, что y=f(x1)
и y=f(x2).
И мы сразу пришли к противоречию,
поскольку x1 x2,
то
x2,
то
либо x1<x2
 f(x1)<
f(x2),
f(x1)<
f(x2),
либо x1>x2
 f(x1)>
f(x2).
f(x1)>
f(x2).

 y
y Y
Y
 единственный x
единственный x X:
y=f(x).
X:
y=f(x).
Аналогичное доказательство приводится для строго-убывающей функции.
А значит, любая строго-монотонная функция на промежутке ненулевой длины имеет обратную функцию.
Теорема 4. (О непрерывности обратной функции.)
Пусть функция f(x) определена на промежутке X ненулевой длины, строго монотонна и непрерывна на X.
Тогда обратная
функция g(y), определённая на Y={f(x),
x X}
имеет тот же характер монотонности
на Y, что и f(x)
на X, и g(y) непрерывна на Y
X}
имеет тот же характер монотонности
на Y, что и f(x)
на X, и g(y) непрерывна на Y
Доказательство.
f: X Y,
g= f-1: Y
Y,
g= f-1: Y X.
X.
I Пусть f(x) строго возрастает на X.
Докажем, что g(y)= f-1(y) строго возрастает на Y.
Возьмём
произвольный y1 Y
и y2
Y
и y2 Y,
y1<y2.
Y,
y1<y2.
Докажем, что
g(y1)< g(y2). Предположим, что
это не так, то есть
 y1,
y2
y1,
y2 Y,
y1<y2, а
g(y1)
Y,
y1<y2, а
g(y1) g(y2).
Но по определению обратной функции g(y)
ставится в соответствие y1
g(y2).
Но по определению обратной функции g(y)
ставится в соответствие y1 Y
единственный x1
Y
единственный x1 X:
f(x1)=y1;
y2
X:
f(x1)=y1;
y2 Y
ставит в соответствие единственный
x2
Y
ставит в соответствие единственный
x2 X:
f(x2)=y2.
X:
f(x2)=y2.
По нашему
предположению y1<y2
 f(x1)<
f(x2).
f(x1)<
f(x2).
Но g(y1)=x1 x2=
g(y2). А тогда в силу строгого
возрастания x1>x2
x2=
g(y2). А тогда в силу строгого
возрастания x1>x2
 f(x1)>
f(x2),
что противоречит условию f(x1)<
f(x2).
x1=x2
f(x1)>
f(x2),
что противоречит условию f(x1)<
f(x2).
x1=x2
 f(x1)=f(x2),
что так же противоречит условию f(x1)<
f(x2).
f(x1)=f(x2),
что так же противоречит условию f(x1)<
f(x2).
II Докажем теперь, что g(y) непрерывна на Y.
Так как f(x) оперделена на промежутке X и непрерывна на нём, то по теореме о промежуточных значениях непрерывной функции Y – промежуток.
А так как
g(y) оперделена на промежетке Y и строго
монотонна на нём, и g: Y X
и X – промежуток, то по теореме 2, g(y)=
f-1(y)
непрерывна на Y.
X
и X – промежуток, то по теореме 2, g(y)=
f-1(y)
непрерывна на Y.
