
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§4. Предельный переход в неравенствах.
Теорема 1.
Пусть
f(х) имеет стандартную область определения
Х, точка хо
лежит внутри
или является концом одного из промежутков,
образующих Х, и пусть
 f(х)=
L.
f(х)=
L.
Если
 число В (число А) и если
число В (число А) и если
 окрестность (хо
окрестность (хо
 хо+
хо+ )
точки хо
такая, что
)
точки хо
такая, что
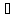 х
х {(хо
{(хо ,
хо)}
,
хо)}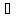 {(
хо,
хо+
{(
хо,
хо+ )}
)} Х:
f(х)
Х:
f(х) В
(соответственно, f(х)
В
(соответственно, f(х) А),
то и L
А),
то и L В
(соответственно, L
В
(соответственно, L А).
А).
Следствие.
Если
 х
х Х:
А
Х:
А f(х)
f(х) В
и L=
В
и L= f(х),
то А
f(х),
то А L
L В.
В.
Теорема 2.
Пусть функции f(х), g(х), h(х) имеют стандартную область определения Х, хо лежит внутри или является концом одного из промежутков, образующих Х.
Если
 -
окрестность (хо
-
окрестность (хо
 хо+
хо+ )
точки хо
(
)
точки хо
( >0)
такая, что
>0)
такая, что
 х
х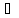 {(хо
{(хо ,
хо)}
,
хо)} {(
хо,
хо+
{(
хо,
хо+ )}
)} Х:
f(х)
Х:
f(х) h(х)
h(х) g(х) и
g(х) и
 f(х)=
f(х)=
 g(х)=L,
то
g(х)=L,
то
 h(х)=L.
h(х)=L.
Теорема 3.
Пусть
f1(х)
и f2(х)
имеют стандартную область определения
Х, хо лежит
внутри или является концом одного из
промежутков, образующих Х, и пусть
L1= f1(х),
L2=
f1(х),
L2= f2(х),
и
f2(х),
и
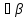 -
окрестность точки хо
(хо
-
окрестность точки хо
(хо
 хо+
хо+ )
такая, что
)
такая, что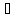 х
х {(хо
{(хо ,
хо)}
,
хо)} {(
хо,
хо+
{(
хо,
хо+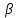 )}
)} Х:
f1(х)
Х:
f1(х) f2(х),
то L1
f2(х),
то L1 L2.
L2.
Теоремы 1, 2, 3 доказываются применением теорем главы 2 о предельном переходе в неравенствах для последовательностей значений заданных функций.
Докажем теорему 2.
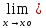 f(х)=
f(х)= g(х)=L.
g(х)=L.
Возьмём
произвольную последовательность {хn}
типа Гейне

 n:
хn
n:
хn Х,
Х,
 n:
хn
n:
хn хо,
хо,
 хn=
хо.
хn=
хо.
Так
как
 хn=
хо
хn=
хо

 >0
>0
 о
о
 n>
n>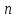 о:
│хn
- хо│<
о:
│хn
- хо│<

 n>
n> о:
хn
о:
хn (хо
(хо
 хо+
хо+ )
и, следовательно, по условию f(хn)
)
и, следовательно, по условию f(хn) h(хn)
h(хn) g(хn).
g(хn).
А так как
 f(хn)=
f(хn)= g(хn)=L
g(хn)=L

 h(хn)=L
(по теореме о „жулике”).
h(хn)=L
(по теореме о „жулике”).
Последовательность
{хn}
типа Гейне была выбрана произвольной,
то по определению предела функции в
точке в смысле Гейне
 h(х)=L.
h(х)=L.
§5. Односторонние пределы функции в точке. (пределы слева и справа)
Определение.
Пусть функция f(х) имеет стандартную область определения Х, точка хо лежит внутри или является правым (левым) концом одного из промежутков, образующих Х.
Говорят,
что f(х) имеет в точке хо
предел слева
(справа)
равный L и пишут
 f(х)=L
(соответственно,
f(х)=L
(соответственно,
 f(х)=L),
если
f(х)=L),
если
(Г)1
 {хn}
{хn} :
(К)1
:
(К)1
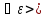 0
0
 >0
>0
 х
х
(х Х,
хn<хо
(соотв. хn>хо),
│x - хо│<
Х,
хn<хо
(соотв. хn>хо),
│x - хо│< ):
):
 f(хn)=L
│f(х)-
L│<
f(хn)=L
│f(х)-
L│<
Так же, как и для обычных пределов (Г)1 и (К)1 эквивалентны.
Односторонние
пределы обладают такими же простейшими
арифметическими свойствами - свойствами,
связанными с неравенствами, что и
обычные пределы (во всех случаях в
доказательстве надо заменит хn хо неравенствами
хn<
хо
(хn>хо)
или х< хо
(соответственно
х>хо)
хо неравенствами
хn<
хо
(хn>хо)
или х< хо
(соответственно
х>хо)
Теорема.
Пусть
f(х) имеет стандартную область определения
Х и точка хо
лежит внутри или является концом
одновременно двух смежных промежутков
из Х, и пусть в точке хо
f(х) имеет равные
односторонние пределы:
 f(х)=
f(х)= f(х)=L
(1).
f(х)=L
(1).
Тогда в точке хо f(х) имеет предел, и он равен L.
Доказательство.
Докажем,
что
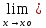 f(х)=L.
f(х)=L.
Из
(1) следует, что
 0
0
 1>0
1>0
 х
(х
х
(х Х,
х< хо,
│x - хо│<
Х,
х< хо,
│x - хо│< 1):
│f(х)- L│<
1):
│f(х)- L│< (2).
(2).
Из (1) следует,
что
 0
0
 2>0
2>0
 х
(х
х
(х Х,
х>хо,
│x - хо│<
Х,
х>хо,
│x - хо│<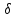 2):
│f(х)- L│<
2):
│f(х)- L│< (3).
(3).
Возьмём
произвольное
 0
и зафиксируем его.
0
и зафиксируем его.
Положим
 =min{
=min{ 1,
1,
 2}>0.
2}>0.
Тогда
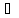 х
(х
х
(х Х,
х
Х,
х хо,
│x - хо│<
хо,
│x - хо│< ):
│f(х)- L│<
):
│f(х)- L│< ,
так как х
,
так как х хо,
то либо х< хо
и тогда справедливо (2), либо х>хо
и тогда справедливо (3).
хо,
то либо х< хо
и тогда справедливо (2), либо х>хо
и тогда справедливо (3).
