
- •Глава I. Действительные числа.
- •§1. Введение.
- •§2. Множества.
- •§3. Понятие множества действительных чисел.
- •§4. Отображения множеств.
- •Глава 2. Числовые последовательности.
- •§1. Понятие числовой последовательности.
- •§2. Бесконечно малые последовательности.
- •§3. Свойства сходящихся последовательностей.
- •Глава 3. Некоторые сведения из математической логики.
- •§1. Предложение.
- •§2. Предикаты.
- •§3. Кванторы.
- •§4. Предельный переход в неравенствах. (Глава 2)
- •§5. Бесконечно большие последовательности.
- •§6. Частичные последовательности (подпоследовательности).
- •§7. Монотонные последовательности.
- •§8. Теорема о вложенных отрезках.
- •§9. Теорема Больцано-Вейерштрасса.
- •§10. Критерий Коши сходимости числовой последовательности.
- •§11. Число .
- •Глава 3. Функции.
- •§1. Понятие числовой функции числового аргумента.
- •§2. Предел функции в точке.
- •§3. Арифметические свойства пределов функций.
- •§4. Предельный переход в неравенствах.
- •§5. Односторонние пределы функции в точке. (пределы слева и справа)
- •§6. Пределы функций на бесконечности.
- •§7. Функции, стремящиеся к бесконечности. (Бесконечно большие функции.)
- •§8. Сравнение бесконечно малых и бесконечно больших функций.
- •§9. Специальные пределы функций.
- •Глава 4. Непрерывность функции.
- •§1. Определение непрерывной функции.
- •§2. Классификация точек разрыва функции.
- •§3. Простейшие свойства непрерывных функций.
- •§4. Некоторые свойства непрерывных функций на промежутке.
- •§5. Условия непрерывности монотонной функции. Обратная функция. Непрерывность обратной функции.
- •Глава 5. Производная функции.
- •§1. Понятие производной функции.
- •§2. Свойства производной функции.
- •§3. Производная обратной функции.
- •§4. Таблица производных.
- •Глава 6. Дифференцируемая функция. Дифференциал.
- •§1. Понятие дифференцируемой функции в точке и дифференциала.
- •§2. Некоторые свойства дифференциала функции в точке.
§10. Критерий Коши сходимости числовой последовательности.
Теорема.
Числовая последовательность сходится тогда и только тогда, когда она удовлетворяет следующему условию Коши:
 0
0
 N=N(
N=N(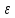 )
)
 n>N
n>N
 m>N:
│xn
- хm│<
m>N:
│xn
- хm│< или
или
 0
0
 N=N(
N=N( )
)
 n>N
и
n>N
и
 p
– натурального: │xn+p
- хn│<
p
– натурального: │xn+p
- хn│< .
.
Доказательство.
1.Необходимость.
{xn}
сходится

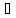 а
а
 0
0
 N
N
 n>N:
│xn
- а│<
n>N:
│xn
- а│< .
.
Возьмём
произвольное
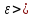 0,
зафиксируем его и проверим выполнение
условия Коши.
0,
зафиксируем его и проверим выполнение
условия Коши.
{xn}
сходится

 а
а
 0,
а значит и для нашего фиксированного
0,
а значит и для нашего фиксированного
 >0,
>0,
 N
N
 n>N:
│xn
- а│<
n>N:
│xn
- а│< .
.
Возьмём
произвольные n>N и m>N и рассмотрим
│xn
- хm│=│xn
-а+а - хm│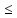 │xn
- а│+│xm
- а│<
│xn
- а│+│xm
- а│< +
+ =
=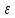 , т.е. условие Коши выполнено.
, т.е. условие Коши выполнено.
2.Достаточность.
Пусть {xn}
удовлетворяет условию Коши

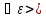 0
0
 n>N,
n>N,
 :
│xn
- хm│<
:
│xn
- хm│< .
.
Докажем, что {xn} сходится.
{xn}
удовлетворяет условию Коши

 0,
а значит и для
0,
а значит и для
 =1>0
=1>0
 N=N(
N=N( )
)
 n>N
и
n>N
и
 m>N:
│xn
- хm│<
m>N:
│xn
- хm│< .
.
Пусть m=N+1>N:
│xn
- хN+1│<1

 n>N:
xN+1
-1<xn<xN+1+1
n>N:
xN+1
-1<xn<xN+1+1

 n>N+1:
xn
n>N+1:
xn (
xN+1
-1, xN+1+1).
(
xN+1
-1, xN+1+1).
Вне этого интервала могут находится х1, х2, …, хN.
Пусть А=min{х1, х2, …, хN, xN+1 -1}
B=max{х1, х2, …, хN, xN+1+1}
Тогда
 n,
n=1, 2, …: xn
n,
n=1, 2, …: xn [А,
В]
[А,
В]
 {xn}
– ограничена, а тогда по теореме
Больцано-Вейерштрасса (§9) из {xn}
можно выделить сходящуюся
подпоследовательность {xnk}.
{xn}
– ограничена, а тогда по теореме
Больцано-Вейерштрасса (§9) из {xn}
можно выделить сходящуюся
подпоследовательность {xnk}.
{xnk}
сходится

 а:
а=
а:
а= xnk.
xnk.
Докажем,
что а=
 xn.
xn.
По
условию Коши,
 0,
0,
 >0,
>0,
 N
N
 n>N
n>N
 m>N: │xn
- хm│<
m>N: │xn
- хm│< .
.
Положим
m=nk k>N.
Тогда xnk
-
k>N.
Тогда xnk
-
 <
xn<
xnk+
<
xn<
xnk+ .
.
Устремим
k +
+ .
Тогда по теореме 1 §4 (предельный переход
в неравенствах для одной последовательности)
получаем а-
.
Тогда по теореме 1 §4 (предельный переход
в неравенствах для одной последовательности)
получаем а- xn
xn а+
а+

 │xn
- а│
│xn
- а│ <
<
 │xn
- а│<
│xn
- а│<
 а=
а=
 xn.
xn.
Определение.
Последовательность {xn}, удовлетворяющая условию Коши, называется фундаментальной.
Из критерия Коши следует, что числовая последовательность сходится тогда и только тогда, когда она фундаментальна.
§11. Число .
Рассмотрим
последовательность {(1+ )n}.
)n}.
Обозначим
элемент этой последовательности
yn=(1+ )n.
)n.
Докажем, что {yn} сходится. Для этого покажем, что она возрастает и ограничена сверху.
Используем формулу Бинома-Ньютона:
yn=
(1+ )n=1+n·
)n=1+n·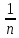 +
+ ·
· +…+
+…+ ·
· +…+
+…+ ·
· =
=1+1+
=
=1+1+ (1-
(1- )+…+
)+…+ (1-
(1- )(1-
)(1-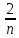 )…(1-
)…(1-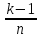 )+…+
)+…+ (1-
(1- )(1-
)(1- )…(1-
)…(1- )
)
yn+1=1+1+ (1-
(1-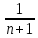 )+…+
)+…+ 1-
1- )…(1-
)…(1-
 )+…+
)+…+ 1-
1- )…(
1-
)…(
1- )+
+
)+
+ (1-
(1- )…
(1-
)…
(1- )
)
-
{yn} строго возрастает.
 n,
n=1, 2, …: yn<yn+1,
так как каждое слагаемое увеличивалось,
ибо
n,
n=1, 2, …: yn<yn+1,
так как каждое слагаемое увеличивалось,
ибо
 >
> и, кроме того, прибавилось ещё одно
положительное слагаемое (последнее).
и, кроме того, прибавилось ещё одно
положительное слагаемое (последнее).
-
{yn} ограничено сверху.
Для
доказательства заменим каждый множитель
(1- )
единицей,
ибо k
)
единицей,
ибо k n
(k-1<n).
n
(k-1<n).
Используя
неравенство k!=1·2·3·…·k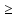 1·2·2·…·2=2k-1,
k=1, 2, …, получим
1·2·2·…·2=2k-1,
k=1, 2, …, получим
yn<1+1+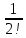 +
+ +…+
+…+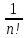 <1+1+
<1+1+ +
+ +…+
+…+ <1+1+
<1+1+ +
+ +…+
+…+ +…=1+
+…=1+ =1+2=3
=1+2=3
Итак,
 n:
yn<3.
n:
yn<3.
Тогда
по теореме о сходимости ограниченной
монотонной последовательности (§7)
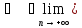 yn=
yn= =sup
{(1+
=sup
{(1+ )n}.
)n}.
 2,7182848…
2,7182848…
Глава 3. Функции.
§1. Понятие числовой функции числового аргумента.
Определение.
Пусть
Х – непустое множество. Х .
.
Говорят,
что на множестве Х задана функция, если
указан закон, согласно которому каждому
элементу х Х
поставлено в соответствие число y.
Х
поставлено в соответствие число y.
Обозначается
функция: y=f(х); х Х.
Х.
При
этом множество Х называется областью
определения функции, а множество Y={y;
y=f(х), х Х
} называется множеством значений функции
y=f(х), х
Х
} называется множеством значений функции
y=f(х), х Х.
Х.
Примеры.
-
Х= {1, 2, …, n, …}
yn=f(n),
n=1, 2, … - числовая последовательность.
– Это функция, областью определения
которой является множество
 всех
натуральных чисел.
всех
натуральных чисел.
-
Х= {1, 2, …, n, …}
f(n)=[an, bn]
-
Х= {
 },
},
 - фиксированный вектор в
- фиксированный вектор в
 3,
3,
 3.
3.
 (
( )=[
)=[ ]
– векторная функция векторного аргумента.
]
– векторная функция векторного аргумента.
g( )=(
)=( ,
,
 )
– числовая функция векторного аргумента.
)
– числовая функция векторного аргумента.
Действия над функциями.
Пусть f1(х) – функция, определённая на Х1.
f2(х) – функция, определённая на Х2.
Тогда на
Х=Х1 Х2
Х2 определены функции:
определены функции:
f1(х) f2(х), f1(х)· f2(х) и
f2(х), f1(х)· f2(х) и
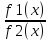 определена на Х
определена на Х {х;
х
{х;
х Х:
f2(х)=0}.
Х:
f2(х)=0}.
Простейшими множествами числовой оси 0х являются промежутки.
Определение.
Промежутком числовой оси называется любое множество вида:
-
[а, b]
 {х; х
{х; х Х:
а
Х:
а х
х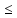 b}.
b}.
отрезок

-
(а, b)
 {х; х
{х; х Х:
а<х<b}.
Х:
а<х<b}.
интервал


-
[а, b)
 {х; х
{х; х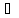 Х:
а
Х:
а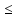 х<b},
х<b},
(а, b] {х; х
{х; х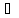 Х:
а<х
Х:
а<х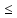 b}.
b}.
полуинтервалы


Неограниченные множества:
-
[а, +
 ]
] {х;
х
{х;
х Х:
х
Х:
х а},
а},
( ,
b]
,
b] {х;
х
{х;
х Х:
х
Х:
х b}.
b}.


-
(а, +
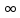 )
) {х;
х
{х;
х Х:
х>а},
Х:
х>а},
( ,
b)
,
b) {х;
х
{х;
х Х:
х<b}.
Х:
х<b}.


-
(
 ,
+
,
+ )
– вся числовая ось.
)
– вся числовая ось.

Определение.
Говорят, что функция y=f(х) имеет стандартную область определения Х, если Х является промежутком ненулевой длины или объединением непересекающихся промежутков ненулевой длины.
