5. Гіперболічний параболоїд.

Гіперболічним параболоїдом називають поверхню, яка в декартовій системі координат визначається рівнянням

.

З

Рис. 13.

дійснимо перетин цієї поверхні з координатною площиною Oyz (це поверхня x=0). Дістанемо рівняння

_.

Це рівняння на площині x=0 визначає параболу, вісь якої направлена вздовж осі Oz вниз з вершиною на початку координат.

Здійснимо перетин цієї поверхні з координатною площиною Oxz (це поверхня y=0). Дістанемо рівняння

Це рівняння на площині y=0 визначає параболу, вісь якої направлена вздовж осі Oz вгору з вершиною на початку координат.

Здійснимо перетин цієї поверхні з площиною x=h.

Це рівняння визначає параболу, у якої вісь направлена по осі Oz вниз, а вершина знаходиться на параболі, яка визначається рівнянням (). При нескінченному зростанні значення величини h вершина параболи також прямує до нескінченності.

Здійснимо перетин цієї поверхні з площиною y=h.

Це рівняння визначає параболу, у якої вісь направлена по осі Oz вгору, а вершина знаходиться на параболі, яка визначається рівнянням (). При нескінченному зростанні значення величини h вершина параболи також прямує до нескінченності.

Тепер розглянемо перетини поверхні з площинами z=h. Підставивши це значення у рівняння дістанемо:

У цьому випадку величина h може приймати будь-яке значення.

Щоб рівняння звести до канонічного вигляду розглянемо два випадки:

h≥0 _{, ;}

h≤0 _, .

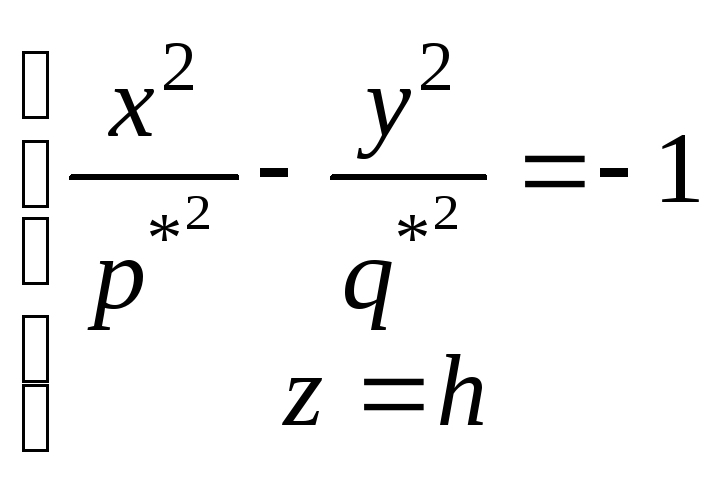
У першому випадку перетином поверхні площинами z=h є гіперболи, які перетинають площину Oxz, а у другому випадку гіперболи, які перетинають площину Oyz.

Якщо h=0, то гіпербола вироджується у пару прямих, що перетинаються та проходять через початок координат.

_.

Таким чином, розглянуті перетини дозволяють зобразити гіперболічний параболоїд у вигляді сідла (Рис. 13).

6. Конус другого порядку.

Конусом другого порядку називають поверхню, яка в декартовій системі координат визначається рівнянням

.

Здійснимо перетин цієї поверхні з координатною площиною Oyz (це поверхня x=0). Дістанемо рівняння

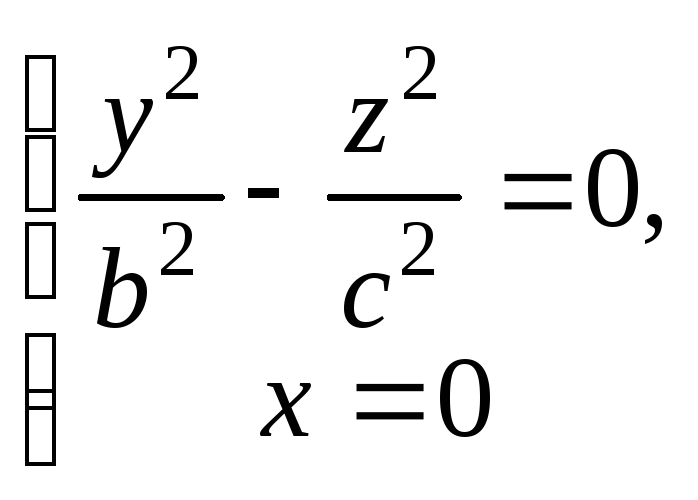
Рис. 14.

яке розпадається на дві прямі, що перетинаються та проходять через початок координат

та _.

Здійснимо перетин цієї поверхні з координатною площиною Oxz (це поверхня y=0). Дістанемо рівняння

яке розпадається на дві прямі, що перетинаються та проходять через початок координат

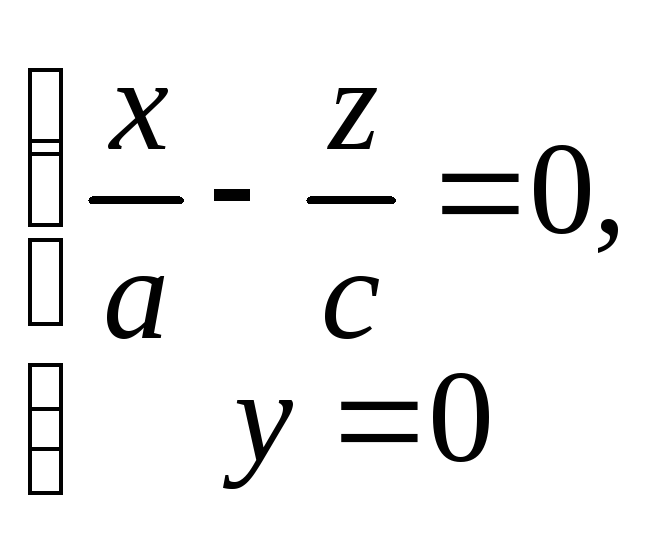та _.

Тепер здійснимо перетин поверхні площинами z=h. Дістанемо

або _,

Це рівняння на площині z=h визначає еліпс, велика піввісь та мала піввісь якої нескінченно зростає при нескінченному зростанні значення величини h.

Якщо h=0, то в перетині поверхні з площиною z=0 буде міститись лише одна точка (0, 0, 0).

Перетин поверхні з площинами x=h або y=h визначить гіперболу.

Існують такі площини Ax+By+Cz+D=0, що в перетині з конічною поверхнею можна отримати також параболу. Ці два останні твердження пропонуємо показати самостійно.

Таким чином, розглянуті перетини дозволяють зобразити конічну поверхню у вигляді рис.14.