Завдання для самостійного розв'язання.
6. Привести до канонічного вигляду рівняння наступних прямих:
а)
б)
7.
Написати канонічне рівняння прямої, що
проходить через точку
та паралельна а) вектору
;
б) прямій
.
8. Визначити чи перетинаються прямі в просторі та знайти кут між ними:
а)
;
б)
.
9. Довести перпендикулярність прямих
та
.
Відповіді.
6.
а)
,
б)
.
7.
а)
,
б)
.
8.
а) не перетинаються,
;
б) перетинаються,
.
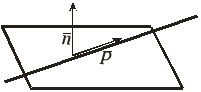
§ 4. Пряма і площина у просторі
Кут
між прямою
та площиною
визначається за формулою:
.
(37)
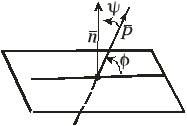
Рис 4.
Пряма
і площина паралельні тоді і тільки тоді,
коли нормаль площини
та напрямний вектор прямої
перпендикулярні, тобто:
;
(38)
Пряма
і площина перпендикулярні тоді і тільки
тоді, коли нормаль площини
та напрямний вектор прямої
паралельні, тобто:
.
(39)
|
Рис 5. Пряма і площина паралельні |
Рис 6. Пряма і площина перпендикулярні |
Точка
перетину прямої і площини.
Для знаходження точки перетину прямої
і площини потрібно скористатись
параметричним рівнянням прямої:
,
,
,
підставити у рівняння площини
замість
,
розв'язати лінійне рівняння відносно
параметру
.
Підставивши знайдене значення
у параметричне рівняння прямої знаходимо
координати точки перетину прямої і
площини.
Приклади.
1.
Знайти точку перетину прямої
і площини
та визначити кут між ними.
Розв'язання.
Параметричне рівняння прямої має вигляд:
,
,
.
Підставимо вирази для
у рівняння площини:
.
Отже
координати точки перетину дорівнюють:
.
Для визначення кута запишемо направляючий
вектор прямої:
та нормальний вектор площини:
.
Скориставшись формулою (37) будемо мати:
.
2.
Записати
рівняння прямої, що проходить через
точку
перпендикулярно до площини
.
Розв'язання.
Будемо шукати рівняння прямої в канонічній
формі (30), де
,
,
– координати точки, через яку проходить
пряма,
– координати направляючого вектора
прямої. В нашому випадку
,
,
.
Оскільки пряма перпендикулярна до
заданої площини, то її направляючий
вектор
,
згідно (39), колінеарний нормальному
вектору площини
.
Тому в якості вектора
для прямої можна взяти нормальний вектор
площини:
,
,
.
Отже, рівняння прямої запишеться у
вигляді:
.
Завдання для самостійного розв'язання.
10.
Записати рівняння площини, що проходить
через точку
перпендикулярно до прямої
а)
,
б)
.
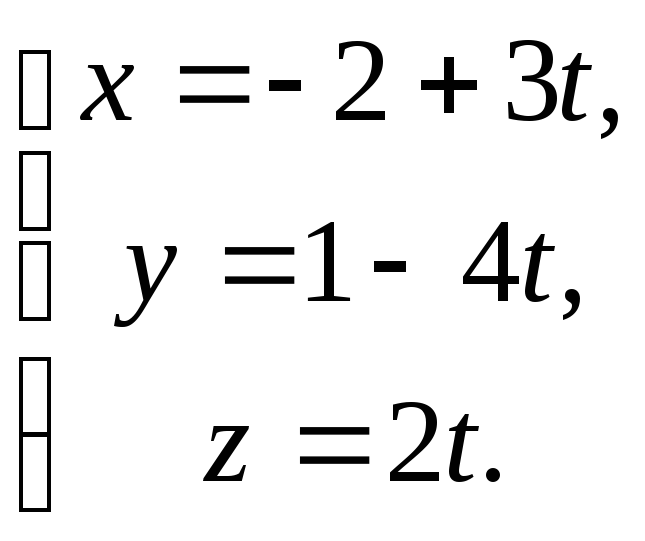11.
Записати рівняння площини, що проходить
через пряму та через точку
,
.
12. Знайти точку перетину прямої і площини та визначити кут між ними, якщо:
а)
;
б)
.
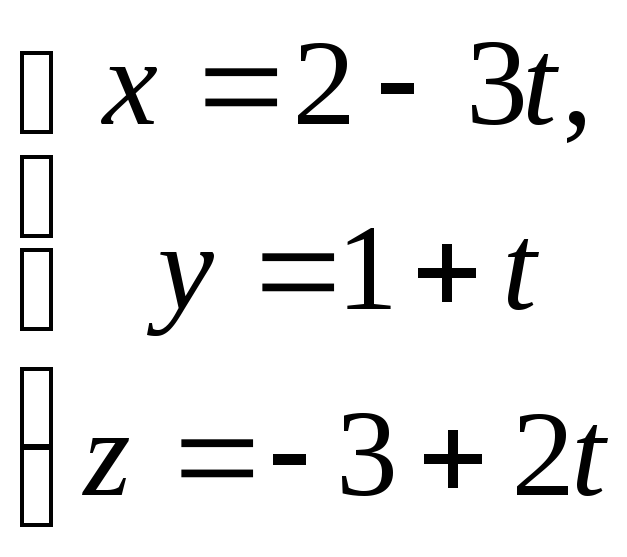
Відповіді.
10.
а)
,
б)
.
11.
.
12.
а)
,
;
б)
,
.
§ 5. Поверхні другого порядку.
Будь яка поверхня в просторі в декартовій системі координат задається в рівнянням
Якщо рівняння не містить якоїсь змінної, наприклад змінної z: F(x,y,z)=0 , то таке рівняння визначає циліндричну поверхню, яка паралельна осі Oz. На площині Oxy рівняння F(x,y,z)=0 визначає деяку лінію l. Щоб отримати циліндричну поверхню слід через кожну точку лінії l провести прямі, паралельні осі Oz.
Наприклад,
якщо на площині Oxy
задано еліпс
,
то в просторі дістанемо поверхню
еліптичного циліндра.
|
Рис. 7. |
Рис. 8. |
Аналогічно будуються циліндричні поверхні для рівнянь, у яких відсутня змінна x або y. У цьому випадку поверхня буде паралельна відповідно осі Ox або Oy.
Поверхні другого порядку – це поверхні, які в декартовій прямокутній системі координат задаються алгебраїчними рівняннями другого порядку. Аналогічно лініям другого порядку на площині існують канонічні рівняння поверхонь другого порядку. Дослідження форм таких поверхонь здійснюється методом паралельних перерізів.
-
Еліпсоїд.
Еліпсоїдом називають поверхню, яка в декартовій прямокутній системі координат задається рівнянням
.
Щоб встановити геометричний вид цієї поверхні, розглянемо перетини її з площинами, перпендикулярними осі Oz: z=h. Підставимо це значення z у рівняння еліпсоїда
.
Оскільки
,
то, щоб виконувалась нерівність
,
необхідно, що величина h
змінювалась в межах –c
≤ h ≤ c. Це означає, що
не існує спільних точок між еліпсоїдом
та площиною z=h,
якщо
.
Тому весь еліпсоїд розміщений в межах
–c ≤ z ≤ c.
Я
Рис
9.
,
то рівняння
має
лише один розв’язок x=0,
y=0.
В перетині еліпсоїда і площин z=c,
z=–c
лише одна точка (0, 0, c)
та (0, 0, –c)
відповідно.
Якщо
,
то рівняння
на площині z=h визначає еліпс
,
,
.
Його велика і мала півосі змінюються в межах
0 ≤ a* ≤ a, 0 ≤ b* ≤ b
залежно від того, яке значення буде приймати величина h. Якщо h = 0, то a* = 0, а якщо h=c, то a* = a.
Аналогічно показується, що весь еліпсоїд розміщений в межах –a ≤ x ≤ a, якщо здійснювати перетин площинами x=h та в межах –b ≤ y ≤ y, , якщо здійснювати перетин площинами y=h та в перетині також будуть відповідні еліпси.
Із вищезазначеного поверхня еліпса матиме вигляд, який зображено на рис 9: