- •Заняття 7 аналітична геометрія в просторі § 1. Прямокутна система координат в просторі
- •Приклади.
- •Завдання для самостійного розв'язання.
- •Приклади.
- •Завдання для самостійного розв'язання.
- •§ 4. Пряма і площина у просторі
- •§ 5. Поверхні другого порядку.
- •Гіперболоїд з однією порожниною.
- •Гіперболоїд з двома порожнинами.
- •Еліптичний параболоїд.
- •Гіперболічний параболоїд.
- •Конус другого порядку.
Заняття 7 аналітична геометрія в просторі § 1. Прямокутна система координат в просторі
Прямокутна
система координат
![]() в просторі визначається трьома взаємно
перпендикулярними осями
в просторі визначається трьома взаємно
перпендикулярними осями
![]() ,
що перетинаються в одній точці
,
що перетинаються в одній точці
![]() і однакову масштабну одиницю. Точка
і однакову масштабну одиницю. Точка
![]() називається початком координат,
називається початком координат,
![]() – віссю абсцис,
– віссю абсцис,
![]() – віссю ординат,
– віссю ординат,
![]() – віссю аплікат.
– віссю аплікат.
Будь-яка
точка простору характеризується єдиним
вектором
![]() .
І навпаки будь-яка трійка чисел (будь-який
вектор) визначає на площині єдину точку.
Така трійка чисел називається координатами
точки
.
І навпаки будь-яка трійка чисел (будь-який
вектор) визначає на площині єдину точку.
Така трійка чисел називається координатами
точки
![]() .
Перше число називається абсцисою, друге
– ординатою, а третє – аплікатою точки.
Початок координат має координати
.
Перше число називається абсцисою, друге
– ординатою, а третє – аплікатою точки.
Початок координат має координати
![]() .
.
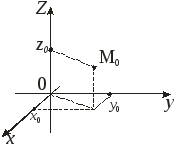
Рис 1
§ 2. Площина у просторі
Запишемо найпоширеніші види рівнянь площини в просторі.
Загальне
рівняння площини перпендикулярна
вектору
![]() .
.
![]() , (20)
, (20)
де
![]() довільні дійсні числа, такі що
довільні дійсні числа, такі що
![]() .
Коефіцієнти
.
Коефіцієнти
![]() визначають вектор нормалі площини
визначають вектор нормалі площини
![]() ,
який перпендикулярний площині.
,
який перпендикулярний площині.
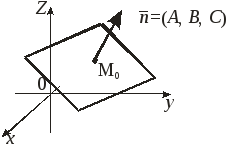
Рис 2
Рівняння
площини, що проходить через задану точку
![]() і перпендикулярна вектору
і перпендикулярна вектору
![]() .
.
![]() .
(21)
.
(21)
Рівняння
площини, що проходить через задану точку
![]() і паралельна двом неколінеарним векторам
і паралельна двом неколінеарним векторам
![]() і
і
![]() .
.
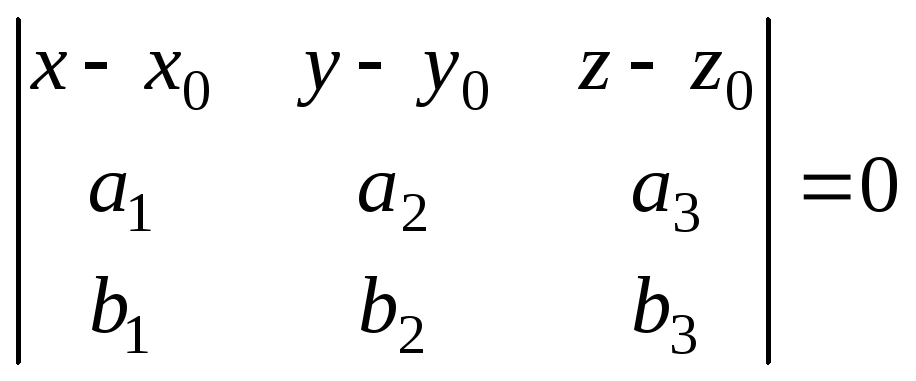 .
(22)
.
(22)
Рівняння
площини, що проходить через три точки
![]() ,
,
![]() ,
,
![]() .
.
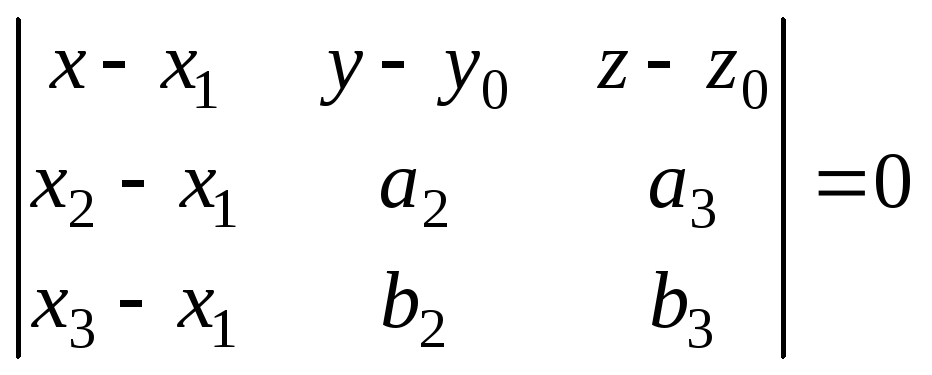 .
(23)
.
(23)
Рівняння площини, "у відрізках на осях"
![]() .
(24)
.
(24)
Неповні рівняння площини.
-
Площина
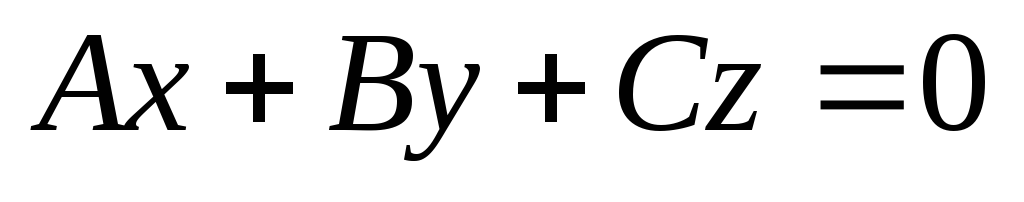 проходить через початок координат.
проходить через початок координат. -
Площина
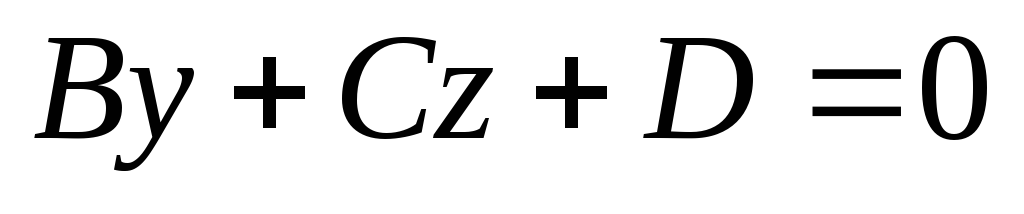 паралельна осі
паралельна осі
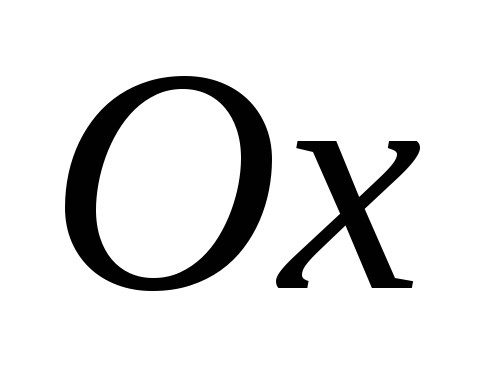 .
. -
Площина
 паралельна осі
паралельна осі
 .
. -
Площина
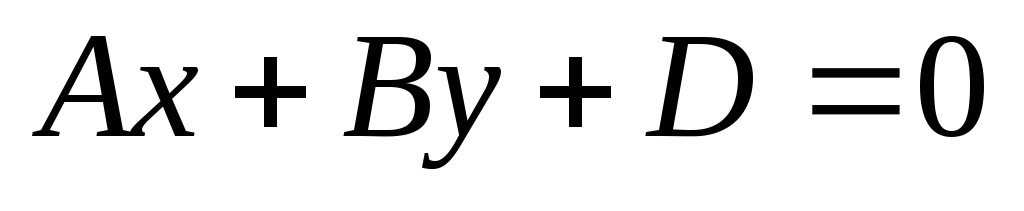 паралельна осі
паралельна осі
 .
. -
Площина
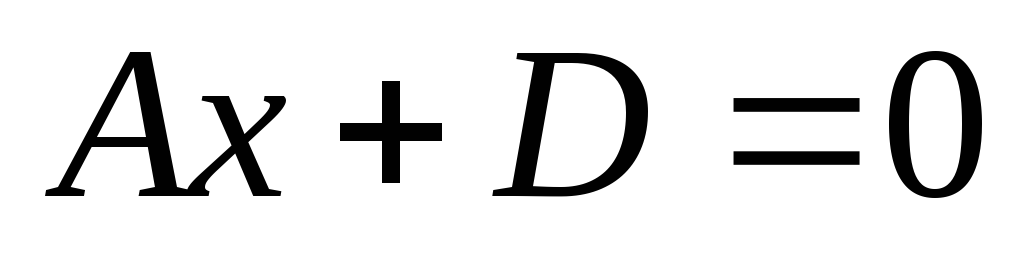 паралельно осям
паралельно осям
 та
та
 ,
або перпендикулярна осі
,
або перпендикулярна осі
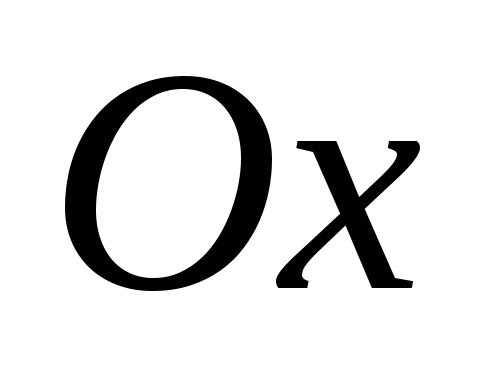 та перетинає її в точці
та перетинає її в точці
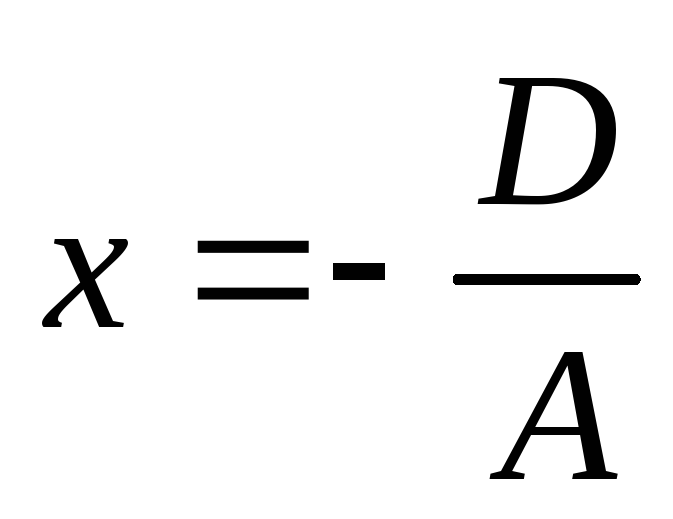 .
. -
Площина
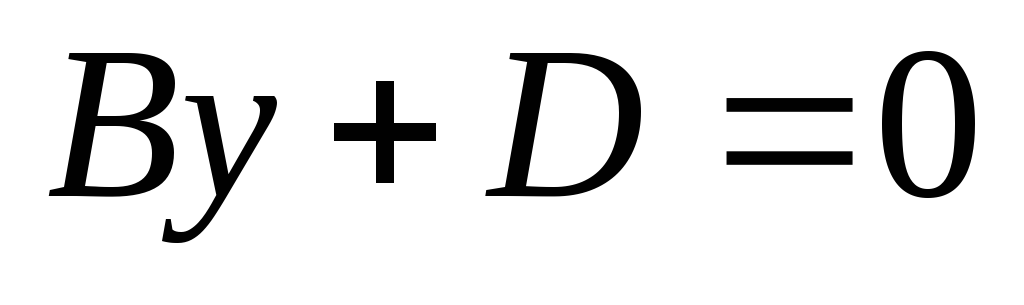 паралельно осям
паралельно осям
 та
та
 ,
або перпендикулярна осі
,
або перпендикулярна осі
 та перетинає її в точці
та перетинає її в точці
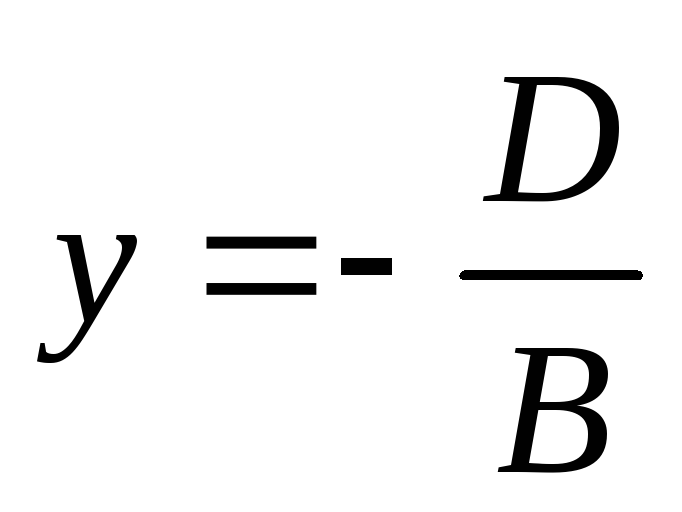 .
. -
Площина
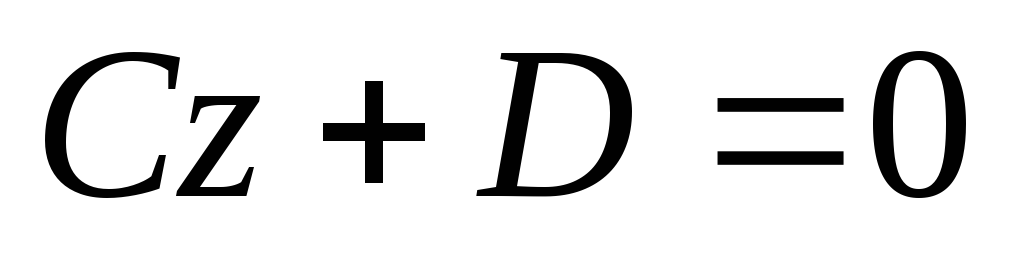 паралельно осям
паралельно осям
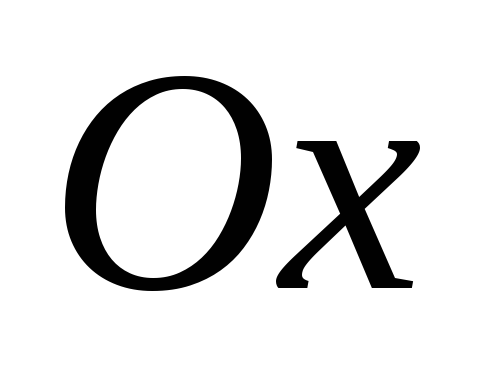 та
та
 ,
або перпендикулярна осі
,
або перпендикулярна осі
 та перетинає її в точці
та перетинає її в точці
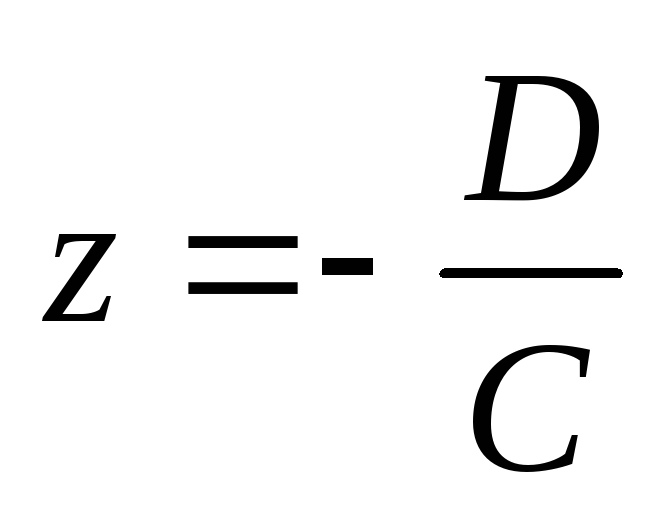 .
.
Взаємне розміщення двох площин
Нехай
площини
![]() задані загальним рівнянням:
задані загальним рівнянням:
![]() :
:
![]() ;
;
![]() ;
;
![]() :
:
![]() ;
;
![]() .
.
Якщо
![]() ,
то дві площини співпадають.
,
то дві площини співпадають.
Умови
паралельності двох площин: Дві площини
паралельні тоді і тільки тоді, коли
паралельні їхні нормалі
![]()
![]() :
:
![]() .
(25)
.
(25)
Умови
перпендикулярності двох площин: Дві
площини перпендикулярні тоді і тільки
тоді, коли перпендикулярні їхні нормалі
![]()
![]() :
:
![]() .
(26)
.
(26)
|
|
|
Рис 3
Кут
між площинами визначається кутом між
нормалями
![]()
![]() :
:
![]() .
(27)
.
(27)
Відстань
від точки
![]() до площини
до площини
![]() становить
становить
![]() .
(28)
.
(28)
Приклади.
1.
Написати рівняння площини, що проходить
через точку
![]() перпендикулярно до вектора
перпендикулярно до вектора
![]() та знайти кут між нею та площиною
та знайти кут між нею та площиною
![]() .
.
Розв'язання. За формулою (20) рівняння площини має вигляд:
![]() .
.
Вектор
нормалі цієї площини –
![]() .
Вектор нормалі заданої площини –
.
Вектор нормалі заданої площини –
![]() .
Косинус кута між цими двома площинами
знайдемо за формулою (27):
.
Косинус кута між цими двома площинами
знайдемо за формулою (27):
![]() .
.
2.
Написати
рівняння площини, що проходить через
три точки
![]() ,
,
![]() ,
,
![]() та знайти відстань від точки
та знайти відстань від точки
![]() до цієї площини.
до цієї площини.
Розв'язання. Скористаємось формулою:
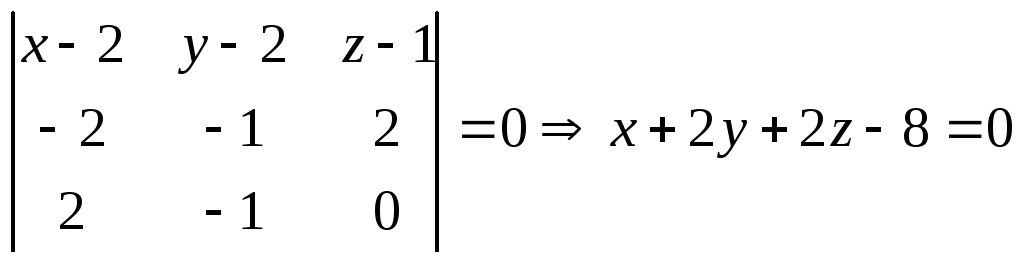 .
.
Відстань від точки до площини знайдемо за формулою ( )
![]() .
.
3.
Написати
рівняння площини, що проходить через
точку
![]() та а) перпендикулярна осям
та а) перпендикулярна осям
![]() ,
,
![]() ,
,
![]() ;
б) паралельна осі
;
б) паралельна осі
![]() та проходить через початок координат.
та проходить через початок координат.
Розв'язання.
а) Скористаємось неповними рівняннями
площин. Якщо площина перпендикулярна
осі
![]() ,
то її рівняння має вигляд
,
то її рівняння має вигляд
![]() .
Враховуючи, що пряма проходить через
точку
.
Враховуючи, що пряма проходить через
точку
![]() остаточно отримаємо
остаточно отримаємо
![]() .
Аналогічно рівняння
.
Аналогічно рівняння
![]() визначає площину, яка проходить через
точку
визначає площину, яка проходить через
точку
![]() перпендикулярно осі
перпендикулярно осі
![]() ,
а рівняння
,
а рівняння
![]() – площину, яка проходить через точку
– площину, яка проходить через точку
![]() перпендикулярно осі
перпендикулярно осі
![]() .
.
б)
Рівняння площини, яка паралельна осі
![]() –
–
![]() .
Оскільки ця пряма ще й проходить через
початок координат та через точку
.
Оскільки ця пряма ще й проходить через
початок координат та через точку
![]() ,
то
,
то
![]() і
і
![]() .
Розв'язком цього рівняння може бути
.
Розв'язком цього рівняння може бути
![]() ,
,
![]() .
Отже рівняння площини, що задовольняє
умовам задачі має вигляд
.
Отже рівняння площини, що задовольняє
умовам задачі має вигляд
![]() .
.