2.4. Символьное решение уравнений

Некоторые уравнения можно решить точно с помощью символьного процессора MathCAD. Делается это очень похоже на численное решение уравнений с помощью вычислительного блока. Присваивать неизвестным начальные значения нет необходимости. Например, символьное решение алгебраического уравнения с одним неизвестным имеет вид:

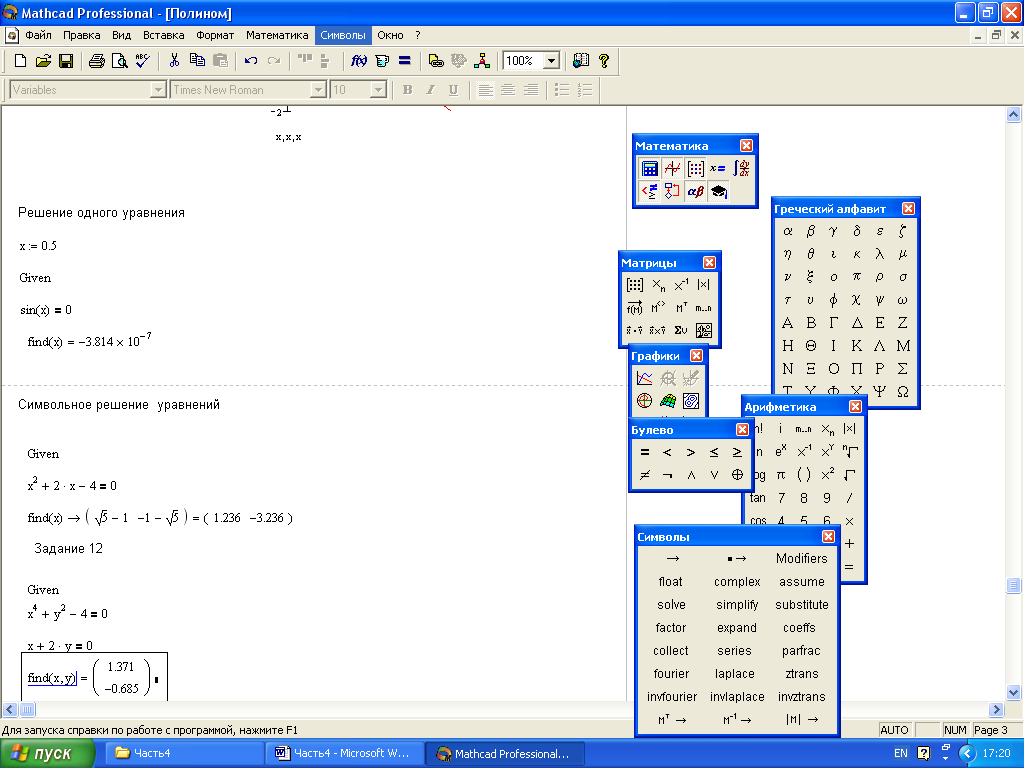
Символьное решение системы алгебраических уравнений можно получить следующим образом:

Задание 12. Найдите символьное решение системы алгебраических уравнений:

x⁴ +y²-4=0

x+2*y=0

Результаты решения запишите в свою папку.

3. Поиск экстремума функции

Задача поиска экстремума функции означает нахождение ее максимума или минимума в некоторой области определения ее аргументов. Ограничения значений аргументов, задающих эту область, как и прочие дополнительные условия, должны быть определены в виде системы неравенств и (или) уравнений. В этом случае говорят о задаче на условный экстремум. Для решения задач поиска максимуму и минимума в MathCAD имеются встроенные функции Minerr, Minimize и Maximize. Все они используют те же градиентные численные методы, что и функция Find для решения уравнений.

• Minimize (f,x₁,…,x_M) – вектор значений аргументов, при которых функция f достигает минимума;

• Maximize(f,x₁,…,x_M) - вектор значений аргументов, при которых функция f достигает максимума.

3.1. Экстремум функции одной переменной

Поиск экстремума функции включает в себя задачи нахождения локального или глобального экстремума. Такие задачи называют еще задачами оптимизации.

Задание 13. Постройте график функции f(x)=x⁴+5·x³-10·x на интервале (-5,2), и найдите глобальные и локальные экстремумы.

1. Откройте новый документ и построите график функции на заданном интервале (рис. 32). Она имеет глобальный максимум на левой границе интервала, глобальный минимум, локальный максимум, локальный минимум и локальный максимум (в порядке слева направо).

2. Анализ графика показывает, что первый локальный минимум находится в вблизи точки x=-3. Использование функции Minimize дает следующие результаты:

Рис. 32. График функции f(x)

3. Второй локальный минимум находится вблизи точки x=1:

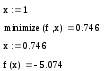
4. Локальный максимум следует искать в районе точки x= -1:

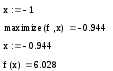
5. Определите значение функции на границах диапазона и рассчитайте глобальные экстремумы.

6. Сохраните полученный документ в своей папке.

3.2. Условный экстремум

В задачах на условный экстремум функции минимизации и максимизации должны быть включены в вычислительный блок, т.е. им должно предшествовать ключевое слово Given. В промежутке между Given и функцией поиска экстремума с помощью булевых операторов записываются логические выражения (неравенства, уравнения), задающие ограничения на значения аргументов минимизируемых функций.

Задание 14. Проделайте следующие операции и сравните результаты с предыдущим заданием:

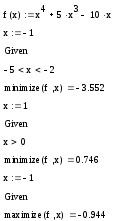
3.3. Экстремум функции многих переменных

Вычисление экстремума функции многих переменных не несет принципиальных особенностей по сравнению с функциями одной переменной.

Задание 15. Найдите экстремум функции двух переменных:

f(x,y)=2· (x-5.07)²+(y-10.03)²-0.2·(x-5.07)³,

выполнив следующие операции:

1. Самостоятельно нарисуйте поверхностный и контурный графики исследуемой функции (рис. 33) и найдите на графиках экстремум функции.

2. С помощью операции присваивания определите функцию и начальные значения аргументов:

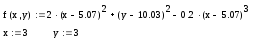
3. Запишите вычислительный блок для определения минимума функции:

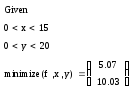
4. Получите минимальное значение функции при рассчитанных значений аргументов:

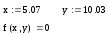
Рис. 33. Поверхностный и контурный графики функции f(x,y)