4.Решение лнду n- го порядка с постоянными коэффициентами и правой специальной частью.

Рассмотрим линейное неоднородное ДУ n-го порядка

, где - заданные непрерывные функции на (,b). Соответствующее ему однородное уравнение имеет вид

Теорема: Общее решение ЛНДУ n-го порядка равно сумме частного решения у* неоднородного уравнения и общего решения соответствующего ему однородного уравнения т.е. .

Частное решение ЛНДУ n-го порядка может быть найдено, если известно общее решение однородного уравнения, методом вариации произвольных постоянных. Оно ищется в виде - частные решения, образующие фундаментальную систему однородного уравнения.

Система уравнений для нахождения неизвестных имеет вид

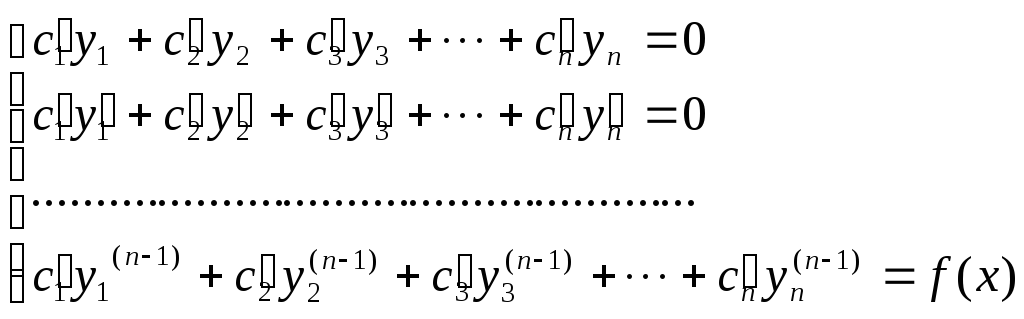
Однако, для ЛНДУ n – го порядка с постоянными коэффициентами, правая часть которого имеет специальный вид, частное решение у* может быть найдено методом неопределенных коэффициентов.

Метод подбора частного решения у* уравнения , а правая часть f(x) имеет специальный вид описанный в п.3 для случая n =2, переносится без всякого изменения и на случай уравнения, имеющего порядок .

Пример:

Найдем ,

Отсюда

Найдем у*; , следовательно

. Тогда , откуда А= -1,В=0 и получим . Следовательно функция является общим решением уравнения.

6. Системы дифференциальных уравнений

Для решения многих практических задач в различных областях науки и техники нередко требуется использовать не одну, а много функций. Нахождение этих функций может привести к нескольким ДУ, каждое из которых содержит независимую переменную . Совокупность всех этих ДУ и образует систему. Системой ДУ называется совокупность ДУ каждое из которых содержит независимую переменную, искомые функции и их производные. Общий вид системы ДУ первого порядка, содержащей n искомых функций , следующий :

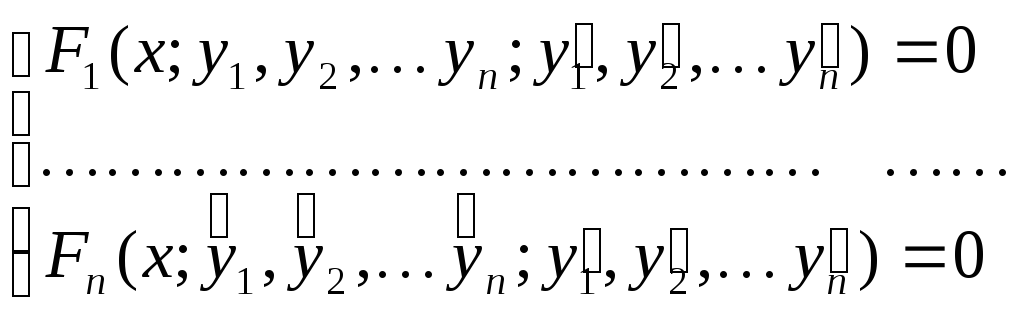
Система ДУ первого порядка, разрешенных относительно производной, т.е. система вида

(1)

называется нормальной системой ДУ . При этом предполагается, что число уравнений равно числу искомых функций.

Замечание: Во многих случаях системы уравнений и уравнения высших порядков можно свести к нормальной системе (1).

Так система трех ДУ второго порядка

описывающая движение точки в пространстве, путем введения новых переменных , и можно привести к нормальной системе ДУ.

Подобную операцию можно производить и с системами уравнений, содержащих производные более старшего порядка. Отсюда следует полезность изучения именно нормальных систем.

Решением системы (1) называется совокупность из n функций удовлетворяющих каждому из уравнений этой системы. Начальные условия для системы (1) имеют вид . (2)

Задача Коши для системы ставится так: найти решение системы уравнений (1) удовлетворяющее начальным условиям (2).Условия существования и единственность решения определяется теоремой Коши.

Теорема Коши: Если в системе (1) все функции непрерывны вместе со своими частными производными по в некоторой области - мерного пространства), то в каждой точке этой области существует, и притом единственное, решение системы, удовлетворяющее начальным условиям (2).

Меняя в области Д точку (т.е. начальные условия) получим бесчисленное множество решений, которое можно записать в виде решения зависящего от n произвольных постоянных :

Это решение является общим, если по заданным начальным условиям (2) можно однозначно определить постоянные , из системы уравнений

Решение, получающееся из общего, при конкретных значениях постоянных () называется частным решением системы (1) .