
- •Содержание
- •Лабораторная работа 1 экспериментальная проверка принципа независимости действия сил
- •Цель работы
- •Основные теоретические положения
- •Принцип независимости действия сил
- •Экспериментальная установка
- •Порядок выполнения контрольной работы
- •5. Составление отчета
- •6. Контрольные вопросы
- •Лабораторная работа 2 испытания на растяжение металлических образцов
- •Цель работы
- •Основные теоретические положения
- •Диаграмма растяжения и ее характерные точки
- •2.2. Форма и размеры образцов
- •Порядок проведения испытания
- •Обработка результатов испытания
- •Составление отчета
- •Контрольные вопросы
- •Лабораторная работа 3 определение перемещений при изгибе балки
- •Цель работы
- •Основные теоретические положения
- •Экспериментальная установка
- •Порядок выполнения лабораторной работы
- •Лабораторная работа 4 определение модуля продольной упругости для стали
- •Порядок выполнения лабораторной работы
- •Составление отчета
- •Контрольные вопросы
- •Лабораторная работа 5 составление кинематической схемы и структурный анализ рычажных механизмов
- •Цель работы
- •Основные теоретические положения
- •Исследуемые механизмы
- •Порядок выполнения работы
- •Плоский механизм
- •Пространственный механизм
- •Составление отчета
- •Контрольные вопросы
- •Лабораторная работа 6 определение механического кпд винтовой пары
- •Цель работы
- •Основные теоретические положения
- •Методика определения среднего кпд винтовой пары. Описание экспериментальной установки
- •Порядок проведения работы
- •Лабораторная работа 7 определение момента трения в подшипниках качения
- •3. Устройство и принцип работы экспериментальной установки
- •Технические характеристики установки:
- •Порядок выполнения работы
- •Лабораторная работа 8 определение механического кпд редуктора с цилиндрическими прямозубыми колесами
- •Устройство прибора дп-3к
- •Порядок выполнения работы
- •Определение передаточного отношения редуктора
- •Тарировка измерительных устройств
- •Определение кпд редуктора
- •Определение кпд редуктора в зависимости от числа оборотов электродвигателя
- •Составление отчета
- •Контрольные вопросы
- •Лабораторная работа 9 определение характеристик винтовых пружин сжатия и растяжения
- •Цель работы
- •Краткие теоретические сведения
- •Устройство и принцип работы экспериментальной установки
- •Порядок выполнения работы
- •Проведение тарировки установки
- •Определение зависимости деформации пружины от нагрузки
- •Определение влияния параметров пружины
- •Составление отчета
- •Контрольные вопросы
- •644099, Омск, ул. Красногвардейская, 9
-
Составление отчета
Отчет о проделанной работе содержит: наименование, цель и порядок проведения работы, эскиз образца до испытания и после разрушения, его материал, диаграмму растяжения, вычерченную в масштабе, с указанием всех характерных точек и масштабов МF и Мl, вычисления основных механических характеристик материала.
-
Контрольные вопросы
-
Цель работы.
-
Какие механические характеристики определяют прочность материала?
-
По каким механическим характеристикам судят о пластических свойствах материала?
-
Виды и размеры стандартных образцов, используемых при испытании на растяжение.
-
Вид диаграммы растяжения для образца из малоуглеродистой стали.
-
Что называется пределом пропорциональности, пределом текучести, пределом прочности? Как определяется их величина по диаграмме растяжения?
-
Что такое условный предел текучести?
-
Условные и истинные напряжения.
-
Что такое наклеп?
-
Остаточные и упругие деформации.
-
Как находятся величины относительного остаточного удлинения и относительного остаточного поперечного сужения ?
-
Как определяются положения осей координат диаграммы растяжения?
Лабораторная работа 3 определение перемещений при изгибе балки
-
Цель работы
Определение опытным путем величин прогибов и углов поворота сечений балки при ее изгибе и сравнение их с теоретическими значениями.
-
Основные теоретические положения
Изгиб – вид нагружения, при котором в поперечных сечениях стержня возникают изгибающие моменты.
Если изгибающий момент является единственным силовым фактором, изгиб называется чистым. Однако чаще всего в поперечных сечениях наряду с изгибающими моментами возникают также и поперечные силы. В этом случае изгиб называется поперечным.
Стержни, работающие в основном на изгиб, часто называют балками.
При изгибе балки согласно гипотезе плоских сечений (гипотезе Бернулли) поперечное сечение элемента балки (рис. 1), плоское и нормальное к его оси до приложения к элементу внешних сил, остается плоским и нормальным к оси и после приложения к элементу нагрузки. Поэтому образование деформаций при чистом изгибе может рассматриваться как результат поворота плоских поперечных сечений друг относительно друга.
l

 l/2
l/2


 z
F
z
F



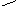 7
7



 A
C
B
A
C
B












![]()





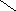 D
L
D
L
![]() 8
8

 yz
yC
К
yz
yC
К
![]()
Рис. 1. Определение прогибов балки
Для определения деформаций воспользуемся уравнением
![]() (1)
(1)
Из курса математики известна связь кривизны плоской кривой с производными функциями этой кривой:
![]() (2)
(2)
Приравняв правые части равенств (1) и (2), получим
 (3)
(3)
Уравнение (3) представляет собой точное дифференциальное уравнение изогнутой оси балки (упругой линии балки). Интегрирование этого нелинейного уравнения представляет большие трудности. Однако для большинства практических задач величиной
![]() (4)
(4)
ввиду
малости деформаций по сравнению с
единицей можно пренебречь. Фактическое
значение углов поворота сечений балки
порядка тысячных долей радиана. Если
даже принять
![]() ,
то и в этом случае величина
,
то и в этом случае величина
![]() ничтожно мала по сравнению с единицей.
ничтожно мала по сравнению с единицей.
Отбросив
величину
![]() ,
получим приближенное дифференциальное
уравнение упругой линии балки
,
получим приближенное дифференциальное
уравнение упругой линии балки
![]() (5)
(5)
интегрирование которого не представляет трудностей.
Выбор знака определяется принятой системой координат.
Для системы координат, показанной на рис. 2, а, момент Мx и кривизна y'' имеют одинаковые знаки и, следовательно, в уравнении (5) следует ставить знак плюс. Для системы координат, представленной на рис.2, б, момент Мx и кривизна y'' имеют противоположные знаки и, следовательно, в уравнении (5) должен быть знак минус.
Перед решением полученного дифференциального уравнения необходимо изгибающий момент Мx представить аналитической функцией от координаты z.
а
 )
y
y
)
y
y




 Mx>0
y''<0
Mx>0
y''<0

y''>0 Mx<0

 z
z
z
z
б


 )
z
z
)
z
z

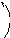


 Mx>0
y''>0
Mx>0
y''>0

y''<0 Mx<0
y y
Рис. 2. Правило знаков при определении прогибов балки
Интегрируя уравнение (5) один раз, получим уравнение углов поворота поперечных сечений
![]() (6)
(6)
Интегрируя второй раз, получим уравнение прогибов балки
![]() (7)
(7)
Постоянные интегрирования С и D находятся из граничных условий, зависящих от вида опорных связей балки. Для балки (рис. 1) граничные условия имеют вид:
при
![]()
![]() ,
при
,
при
![]()
![]()
![]() (8)
(8)
Изгибающий
момент в сечении z
![]() .
.
