
- •1. Дати стислу характеристику ситуації в поняттях і термінах теорії статистичних рішень.
- •Критерій Лапласа
- •Критерій Вальда
- •1.1Матриця виграшів
- •1.2 Критерій Лапласа
- •1.3 Критерій Вальда
- •2.Стисла характеристика ситуації в поняттях і термінах теорії масового обслуговування.
- •2.1 Розгляд усіх можливих варіантів побудови сто.
- •Параметри та характеристики функціонування смо
- •3.Визначення термінів окупності модернізованих варіантів
- •Економічні показники функціонування смо
- •4.Стисла характеристика сітьового планування управлінням
- •4.1.Розроблення сітьового графіку виконання комплексу робіт.
- •4.2 Табличний метод
- •Список використаної літератури
Зміст
ВСТУП 5
1. Дати стислу характеристику ситуації в поняттях і термінах теорії статистичних рішень. 6
Критерій Лапласа 7
Критерій Вальда 7
1.1Матриця виграшів 10
1.2 Критерій Лапласа 10
1.3 Критерій Вальда 11
2.Стисла характеристика ситуації в поняттях і термінах теорії масового обслуговування. 11
2.1 Розгляд усіх можливих варіантів побудови СТО. 14
3.Визначення термінів окупності модернізованих варіантів 19
4.Стисла характеристика сітьового планування управлінням 21
4.1.Розроблення сітьового графіку виконання комплексу робіт. 23
В1 25
Пошук спонсорів 2 25
В2 25
Купівля землі 3 25
В3 25
Проектування СТО 1 25
В4 25
Заливка фундаменту під приміщення 25
В5 25
Демонтажні роботи 25
В6 25
Зварювальні роботи 25
В7 25
Цементна кладка 25
В8 25
Облицювання фасаду 25
В9 25
Електричні роботи 25
В10 25
Асфальтування прилеглих доріг 25
В11 25
Кошторисна документація 25
В12 25
Отримання ліценції 25
В 13 25
Купівля і завезення обладнання 25
В14 25
Відкриття 25
В15 25
Найм працівників 25
4.2 Табличний метод 26
4.2.1Середня кількість зайнятих бригад 27
4.2.2Дисперсія зайнятості бригад 27
4.2.3Середня кількість незайнятих бригад 27
ВИСНОВОК 28
СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ 29
ВСТУП
Мета курсового проекту - застосування теоретичних та практичних знань основ теорії ігор та статистичних рішень для вибору і обґрунтування управлінських рішень в умовах невизначеності, розрахунок параметрів функціонування вибраних варіантів згідно теорії масового обслуговування (ТМО), вибір варіанту, відповідно до результатів розрахунку, розробка календарного плану виконання прийнятого рішення за допомогою сітьового управління плануванням.
Об’єкт дослідження – станція технічного обслуговування (СТО). Інтервали прибуття автомобілів на обслуговування та тривалість обслуговування є випадковими величинами. Передбачається витратити певні кошти на будівництво СТО та придбання обладнання для ремонту і одержати певний дохід від її роботи.
Предмет інженерних розрахунків – обґрунтування вибору рішення в умовах гри з природою; визначення основних характеристик процесів масового обслуговування в обслуговуючій системі, яку представляє собою СТО; розрахунок терміну окупності по декількох варіантах, розробка календарного плану виконання робіт та його оптимізація.
1. Дати стислу характеристику ситуації в поняттях і термінах теорії статистичних рішень.
В теорії ігор розглядаються задачі прийняття рішень в умовах невизначеності, викликаної поведінкою розумного противника, який здійснює найменш вигідні для нас дії.
Але існує невизначеність, пов'язана не з протидією противника, а з недостатньою про-інформованістю про умови проведення операції. Наприклад, може бути заздалегідь невідома погода в районі проведення операції, ціна на певний товар, рівень інтенсивності на ділянці автомагістралі.
Такі умови проведення операції залежать від дійсності, яку прийнято називати природою (деколи - середовищем), поведінка якої невідома, але не містить свідомої протидії. Моделі таких операцій називають іграми з природою. Задачами прийняття рішень в умовах гри з природою займається теорія статистичних рішень. Якщо невизначеність пов’язана з нестачею інформації про ситуацію,то використовують математичні моделі,так звані ігри з природою.
Математичною моделлю такої гри є матриця виграшів,яку складають на основі інформації про виграші гравця при різних станах природи. Під станами природи розуміють умови прийняття рішення та міри володіння інформацією про ситуацію.
В умовах гри з природою керуються вирішальними правилами. Це правила,що дозволяють визначити рішення,яке має перевагу над іншими за певним критерієм. Вони відбивають поінформованість відповідальної особи про можливі наслідки вибраних рішень і про переваги тих чи інших наслідків.
Основою для побудови вирішальних правил служить інформація для відповідальної особи про переваги різних альтернатив.
Існує ряд критеріїв для вибору оптимальної стратегії .
Критерій Лапласа
Критерій
Лапласа називають ще принципом
недостатнього обг
рунтування. Його
застосовують, коли імовірності станів
природи невідомі.
У такому випадку всі стани природи
вважають рівноімовірнісними: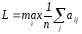
Матрицю виграшів доповнюють ще одним стовпчиком, що містить середнє значення кожного рядка. Вибирають той варіант стратегій, в рядку якого стоїть найбільше значення цього стовпчика.
Критерій Вальда
Критерій Вальда використовує вирішальне правило, що відображає позицію крайньої обережності, песимізму, тому має ще назву ‹‹ критерій обережного спостерігача ›› або ж ‹‹ максимінний критерій ››. Особа, яка приймає рішення, орієнтується на найменш сприятливий випадок і приписує кожному варіанту найгірший з можливих результатів, потім вибирає серед них найбільш вигідний, тобто очікує найкращого результату серед найгірших.
Оптимальна стратегія буде та, що гарантує виграш не менший, ніж
‹‹ нижня ціна ›› гри з природою. Вирішальне правило має вид:
W= max min aіj
i j
Матрицю виграшів доповнюють іще одним стовпчиком з найменших результатів кожного рядка. Вибирають той варіант стратегій, у рядку якого стоїть найбільше значення цього стовпчика.
Критерій застосовують в умовах, коли гру з природою ведуть як гру з розумним противником, тобто передбачають найбільш несприятливий стан природи. Вибране таким чином рішення цілком виключає ризик. Це означає, що особа, яка приймає рішення, не може зіткнутися з гіршим результатом, ніж той, на який він орієнтується. Які би умови, тобто стани природи, не зустрілися, відповідний результат не буде нижчий ніж W.
Критерій Севіджа
Застосовують у ситуації, коли потрібно звести ризик до мінімуму. Для кожного варіанту особа, яка приймає рішення, оцінює втрати в порівнянні з найкращим можливим результатом, а потім із сукупності найгірших результатів вибирає кращий згідно з вирішальним правилом. Це відповідає позиції відносного песимізму.
Оптимальна стратегія буде та, при якій величина ризику в найгірших умовах (тобто коли ризик найбільший) мінімальна. Вирішальне правило має вид:
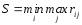
Кожний елемент матриці виграшів віднімають від найбільшого результату відповідного стовпчика р і з цих різниць будують матрицю ризиків, яку доповнюють стовпчиком найбільших ризиків. Вибирають ту стратегію, у рядку якої стоїть найменше для цього стовпчика значення. Ризик — величина додатна:
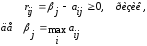
її можна трактувати як максимальний додатковий виграш, якого можна було б досягти, якби в стані S, замість стратегії А, вибрати іншу, оптимальну для цього стану стратегію.
Критерій такий же песимістичний, як і критерій, з орієнтацією на ризик, тому ще називається «критерій мінімізації ризиків».
Якщо ж орієнтуються на величину, обернену до величини ризику то одержують іншу модифікацію критерію Севіджа — «критерій мінімізації жалкувань»:
Критерій Гурвіца
Передбачає більш урівноважений вибір між позиціями крайнього оптимізму і крайнього песимізму. Вирішальне правило має вид:
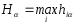
де а— коефіцієнт довіри; 0<а<1;
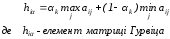
Матрицю виграшів доповнюють стовпчиком значень елементів матриці Гурвіца — це сума середньозважених найбільшого і найменшого
результатів для кожного рядка. Вибирають стратегію, у рядку якої стоїть найбільший елемент матриці Гурвіца.
