Примеры

1. Прямая задана общими уравнениями Написать ее канонические уравнения, а также уравнение ее проекций на координатные плоскости.

Решение. Т. к. то для нахождения точки прямой приведем исходные уравнения к виду

Полагая z равным произвольному числу , например из данной системы найдем , , т. е. .

В качестве направляющего вектора прямой может быть взят вектор , где ,  – нормальные векторы плоскостей, линией пересечения которых является заданная прямая. Таким образом,

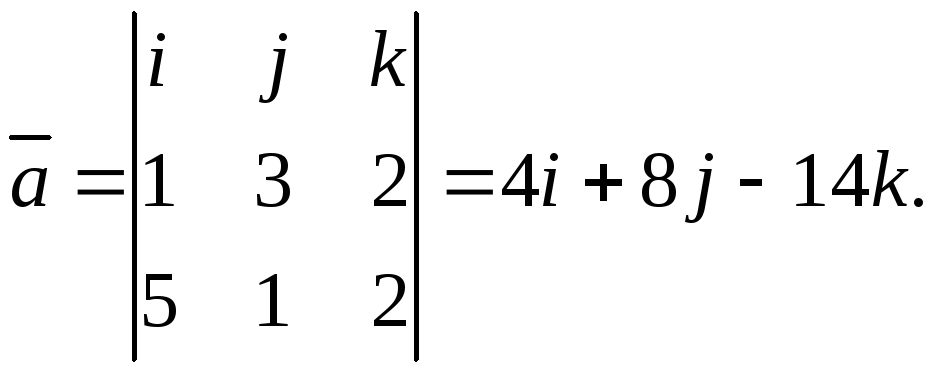
По формуле (1.30) записываем искомые канонические уравнения

или .

Полученная пропорция эквивалентна системе трех уравнений описывающих три плоскости, проектирующие прямую на координатные плоскости и соответственно (уравнения прямой в проекциях).

2. Составить параметрическое уравнение прямой, проходящей через точку перпендикулярно плоскости .

Решение. Нормальный вектор плоскости параллелен искомой прямой и, значит, его можно взять в качестве направляющего вектора этой прямой. Согласно соотношениям (1.31), параметрические уравнения искомой прямой есть

3. Дан треугольник с вершинами . Составить уравнение прямой, на которой лежит медиана, проведенная из вершины В.

Решение. Используя формулы деления отрезка пополам, находим середину отрезка АС – точку Cоставим уравнение прямой, проходящей через две точки В и D, используя формулу (1.33): или .

4. Из начала координат опустить перпендикуляр на прямую

Решение. Используя условие (1.41) перпендикулярности прямой и плоскости и полагая составим уравнение плоскости, проходящей через начало координат и перпендикулярной заданной прямой. Это уравнение имеет вид .

Найдем точку пересечения этой плоскости и данной прямой. Параметрические уравнения прямой запишутся так: ; ; . Для определения t подставим выражения для в уравнение плоскости: откуда Координаты точки пересечения

Остается составить уравнение прямой, проходящей через начало координат и через точку М.

Используя соотношение (1.33), получим или

5. Составить уравнение прямой, проходящей через точку и пересекающей ось под прямым углом.

Решение. Так как прямая перпендикулярна оси и пересекает ее, то она проходит через точку Составив уравнение прямой, проходящей через точки и по формуле (1.33), получаем

6. Найти точку , симметричную точке относительно плоскости

Решение. Искомая точка принадлежит прямой , проведенной из точки перпендикулярно плоскости Р. Уравнения прямой , параллельной вектору и проходящей через точку имеют вид или в параметрическом виде:

Найдем точку пересечения прямой и плоскости, подставляя выражения для в уравнение плоскости. Найдем , откуда

Воспользовавшись формулами деления отрезка пополам, найдем координаты симметричной точки: откуда , , Следовательно, .

7. Дана прямая и вне ее точка . Найти точку , симметричную точке относительно данной прямой.

Решение. Уравнение плоскости, проецирующей точку на данную прямую, имеет вид .

В качестве нормального вектора плоскости, перпендикулярной прямой, можно взять направляющий вектор данной прямой

Тогда получим или

Найдем проекцию точки на прямую, для чего совместно решим систему уравнений (параметрические уравнения прямой). Найдем , отсюда Тогда координаты симметричной точки можно найти, используя формулы для координат середины отрезка, т. е. откуда

8. Через прямую провести плоскость, параллельную прямой

Решение. Запишем уравнения первой из заданных прямых с помощью уравнений двух плоскостей, проецирующих ее соответственно на плоскости и : или или

Уравнение пучка плоскостей, проходящих через эту прямую, имеет вид

или

Используя условие параллельности прямой и плоскости, определим так, чтобы соответствующая плоскость пучка была параллельна второй из заданных прямых.

Имеем или откуда Таким образом, искомая плоскость определяется уравнением .

9. Найти уравнение проекции прямой на плоскость

Решение. Запишем уравнения заданной прямой в виде уравнений двух плоскостей, проецируюших ее соответственно на плоскости и

или или

Уравнение пучка плоскостей, проходящих через данную прямую, запишется в виде: или

Используя условие перпендикулярности плоскостей, выберем из этого пучка плоскость, проецирующую данную прямую на заданную плоскость. Имеем или откуда Итак, уравнение проецирующей плоскости имеет вид или

Искомую проекцию можно определить как линию пересечения двух плоскостей – заданной и проецирующей:

Приведя эти уравнения прямой к каноническому виду, окончательно получим

10. Заданы скрещивающиеся прямые

и

Найти расстояние между прямыми и написать уравнения общего перпендикуляра L к этим прямым.

Решение. Найдем уравнение плоскости Р, проходящей через прямую параллельно прямой . Точка лежит на прямой и, следовательно, принадлежит искомой плоскости Р. В качестве нормального вектора к этой плоскости возьмем вектор

Уравнение плоскости Р: или

Расстояние равно расстоянию от любой точки прямой , например, точки , до плоскости Р. Нормальное уравнение плоскости имеет вид откуда

Для того чтобы составить уравнения общего перпендикуляра L, найдем уравнения плоскостей и , проходящих через заданные прямые и соответственно и перпендикулярных плоскости Р.

Имеем и откуда :  Аналогично, и откуда :  Cледовательно,

– общие уравнения прямой

11. Найти угол между прямыми и

Решение. Направляющий вектор прямой а где Откуда следует, что . Так как то

12. Дан треугольник с вершинами , , . Составить параметрические уравнения прямой, на которой лежит его высота, проведенная из точки В.

Решение. Эту прямую можно рассматривать как линию пересечения двух плоскостей: плоскости, проходящей через три точки , и плоскости, проходящей через точку В перпендикулярно к вектору . Составим их уравнения:

Следовательно, данная прямая определяется уравнениями:

Приведем эти уравнения к параметрическому виду. Нам известна точка В, через которую проходит данная прямая. Найдем координаты направляющего вектора Так как , , то или . Следовательно, параметрические уравнения прямой имеют вид: