1°. Эллипс.

Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек и этой плоскости, называемых фокусами, есть величина постоянная, равная , , большая, чем расстояние между фокусами .

Е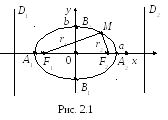сли оси координат расположены по отношению к эллипсу так, как на рис. 2.1, а фокусы эллипса находятся на оси на равных расстояниях от начала координат в точках и , то получится простейшее (каноническое) уравнение эллипса:

, (2.2)

где – большая, – малая полуось эллипса, причем , и ( – половина расстояния между фокусами) связаны соотношением .

Точки , . , называются вершинами эллипса, оси симметрии и – главными осями, а центр симметрии 0 – центром эллипса.

Векторы и называются фокальными радиус-векторами, а числа и – фокальными радиусами точки , принадлежащей эллипсу (в силу определения эллипса для любой его точки ). В частном случае фокусы и совпадают с центром, а каноническое уравнение имеет вид , или , т. е. описывает окружность радиуса с центром в начале координат.

Форма эллипса (мера его сжатия) характеризуется его эксцентриситетом (; при эллипс является окружностью, а т. к. , то ).

Прямые и , перпендикулярные главной оси и проходящие на расстоянии от центра, называются директрисами эллипса.

Фокальные радиусы-векторы выражаются через абсциссу точки эллипса по формулам и .

Если центр эллипса с полуосями и смещен в точку , то его каноническое уравнение имеет вид

. (2.3)

Примеры

1. Какую линию определяет уравнение ?

Разделим данное уравнение почленно на 12: . Сравнивая полученное уравнение с уравнением (2.2), заключаем, что оно определяет эллипс с полуосями , . Найдем фокусы этого эллипса. Так как , то , . Следовательно, фокусы эллипса находятся в точках , .

2. Даны координаты точек , и радиус окружности , центр которой находится в начале координат. Требуется:

а) составить каноническое уравнение эллипса, проходящего через данные точки и ;

б) найти полуоси, фокусы и эксцентриситет этого эллипса;

в) найти все точки пересечения эллипса с данной окружностью;

г) построить эллипс и окружность.

Решение.

а) Пусть – искомое уравнения эллипса. Этому уравнению должны удовлетворять координаты данных точек. Следовательно, подставляя координаты точек, получим Отсюда находим , . Итак, уравнение эллипса имеет вид .

б) , – соответственно большая и малая полуоси эллипса. Для эллипса , значит , откуда . Следовательно, , – соответственно левый и правый фокусы эллипса. Эксцентриситет эллипса .

в) Найдем точки пересечения эллипса с данной окружностью. Уравнение окружности . Решая систему уравнений получим , , . Но , значит , откуда . Итак, существуют две точки пересечения эллипса и окружности и .

г) Построить эллипс и окружность.

3. Большая ось эллипса равна 12, а директрисами его служат прямые . Найти уравнение эллипса и его эксцентриситет.

Решение. По условию . Из уравнений директрис и формулы находим . Тогда . Следовательно, искомое уравнение эллипса есть , а эксцентриситет его .

4. Эллипс касается оси в точке и пересекает ось в точках и . Зная, что оси эллипса параллельны осям координат, составить его уравнение.

Решение. Будем искать уравнение эллипса в виде (2.3). Так как эллипс касается оси , то . Далее, , т. к. прямая параллельна оси и отсекает на оси отрезок . Следовательно, уравнение эллипса имеет вид . Полуось . В таком случае получим – уравнение эллипса. Найдем . Так как лежит на эллипсе, то ее координаты удовлетворяют его уравнению, т. е. . Итак, искомое уравнение эллипса .