Динамические массивы

Во всех вышеприведенных примерах объявлялись статические массивы, поскольку нижняя граница равна нулю по определению, а верхняя всегда задавалась в этих примерах константой. Напомню, что в C# все массивы, независимо от того, каким выражением описывается граница, рассматриваются как динамические, и память для них распределяется в "куче". Полагаю, что это отражение разумной точки зрения: ведь статические массивы, скорее исключение, а правилом является использование динамических массивов. В действительности реальные потребности в размере массива, скорее всего, выясняются в процессе работы в диалоге с пользователем.

Чисто синтаксически нет существенной разницы в объявлении статических и динамических массивов. Выражение, задающее границу изменения индексов, в динамическом случае содержит переменные. Единственное требование - значения переменных должны быть определены в момент объявления. Это ограничение в C# выполняется автоматически, поскольку хорошо известно, сколь требовательно C# контролирует инициализацию переменных.

Приведу пример, в котором описана работа с динамическим массивом:

public void TestDynAr()

{

//объявление динамического массива A1

Console.WriteLine("Введите число элементов массива A1");

int size = int.Parse(Console.ReadLine());

int[] A1 = new int[size];

Arrs.CreateOneDimAr(A1);

Arrs.PrintAr1("A1",A1);

}//TestDynAr

В особых комментариях эта процедура не нуждается. Здесь верхняя граница массива определяется пользователем.

Многомерные массивы

Уже объяснялось, что разделение массивов на одномерные и многомерные носит исторический характер. Никакой принципиальной разницы между ними нет. Одномерные массивы -это частный случай многомерных. Можно говорить и по-другому: многомерные массивы являются естественным обобщением одномерных. Одномерные массивы позволяют задавать такие математические структуры как векторы, двумерные - матрицы, трехмерные - кубы данных, массивы большей размерности - многомерные кубы данных. Замечу, что при работе с базами данных многомерные кубы, так называемые кубы OLAP, встречаются сплошь и рядом.

В чем особенность объявления многомерного массива? Как в типе указать размерность массива? Это делается достаточно просто, за счет использования запятых. Вот как выглядит объявление многомерного массива в общем случае:

<тип>[, ... ,] <объявители>;

Число запятых, увеличенное на единицу, и задает размерность массива. Что касается объявителей, то все, что сказано для одномерных массивов, справедливо и для многомерных. Можно лишь отметить, что хотя явная инициализация с использованием многомерных константных массивов возможна, но применяется редко из-за громоздкости такой структуры. Проще инициализацию реализовать программно, но иногда она все же применяется. Вот пример:

public void TestMultiArr()

{

int[,]matrix = {{1,2},{3,4}};

Arrs.PrintAr2("matrix", matrix);

}//TestMultiArr

Давайте рассмотрим классическую задачу умножения прямоугольных матриц. Нам понадобится три динамических массива для представления матриц и три процедуры, одна из которых будет заполнять исходные матрицы случайными числами, другая - выполнять умножение матриц, третья - печатать сами матрицы. Вот тестовый пример:

public void TestMultiMatr()

{

int n1, m1, n2, m2,n3, m3;

Arrs.GetSizes("MatrA",out n1,out m1);

Arrs.GetSizes("MatrB",out n2,out m2);

Arrs.GetSizes("MatrC",out n3,out m3);

int[,]MatrA = new int[n1,m1], MatrB = new int[n2,m2];

int[,]MatrC = new int[n3,m3];

Arrs.CreateTwoDimAr(MatrA);Arrs.CreateTwoDimAr(MatrB);

Arrs.MultMatr(MatrA, MatrB, MatrC);

Arrs.PrintAr2("MatrA",MatrA); Arrs.PrintAr2("MatrB",MatrB);

Arrs.PrintAr2("MatrC",MatrC);

}//TestMultiMatr

Три матрицы - MatrA, MatrB и MatrC - имеют произвольные размеры, выясняемые в диалоге с пользователем, и использование для их описания динамических массивов представляется совершенно естественным. Метод CreateTwoDimAr заполняет случайными числами элементы матрицы, переданной ему в качестве аргумента, метод PrintAr2 выводит матрицу на печать. Я не буду приводить их код, похожий на код их одномерных аналогов.

Метод MultMatr выполняет умножение прямоугольных матриц. Это классическая задача из набора задач, решаемых на первом курсе. Вот текст этого метода:

public void MultMatr(int[,]A, int[,]B, int[,]C)

{

if (A.GetLength(1) != B.GetLength(0))

Console.WriteLine("MultMatr: ошибка размерности!");

else

for(int i = 0; i < A.GetLength(0); i++)

for(int j = 0; j < B.GetLength(1); j++)

{

int s=0;

for(int k = 0; k < A.GetLength(1); k++)

s+= A[i,k]*B[k,j];

C[i,j] = s;

}

}//MultMatr

В особых комментариях эта процедура не нуждается. Замечу лишь, что прежде чем проводить вычисления, производится проверка корректности размерностей исходных матриц при их перемножении, - число столбцов первой матрицы должно быть равно числу строк второй матрицы.

Обратите внимание, как выглядят результаты консольного вывода на данном этапе работы (рис. 11.2).

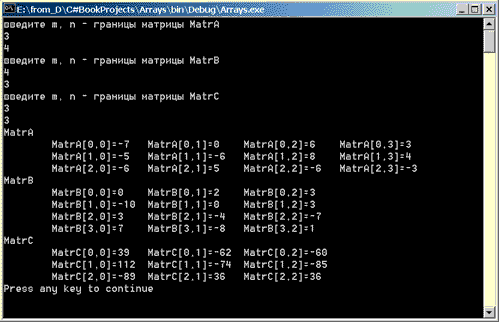Рис. 11.2.  Умножение матриц