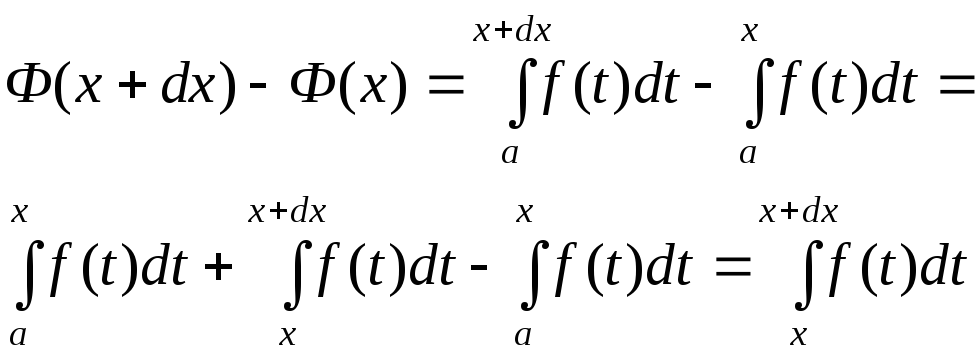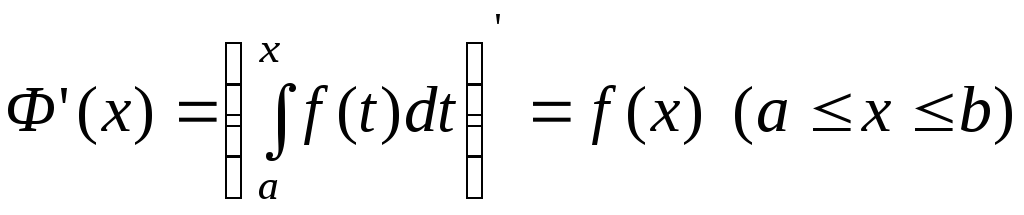Упражнения

1. Пусть отрезок [а; b] оси ox – материальная нить, у которой - заданная линейная плотность вещества, распределенного по этой нити (линейная плотность - это масса единицы длины). Получить формулу для массы всей нити.

Ответ: (14)

2. Пусть – объем тела вращения, образованного вращением криволинейной трапеции (рис.1(а)) вокруг оси ox . Получить формулу для объема этого тела.

Ответ: (15)

3. Пусть – длина участка кривой с абсциссами концов и (рис. 5.1(а)). Получить формулу для длины этого участка.

Ответ: (16)

Свойства и вычисление определенных интегралов.

Начнем с того, что введем понятие определенного интеграла без привязки его к каким-либо геометрическим, физическим и экономическим задачам (что было сделано выше ). То есть введем его сугубо математически.

Пусть - некоторая непрерывная функция, заданная на некотором числовом промежутке [а; b] оси ox. Разобьем его на бесконечно большое число бесконечно малых участков длиной и выберем на каждом некоторую точку . Так как каждый из этих участков бесконечно мал (то есть фактически представляет собой точку), то и есть эта точка. Тогда - бесконечно малое число (смысл его зависит от смысла функции и может быть самым разным - см. предыдущий параграф). А сумма всех этих бесконечно малых чисел называется определенным интегралом

(17)

от функции с пределами интегрирования и (нижним и верхним).

Ниже мы покажем, что при непрерывной подынтегральной функции и конечных пределах интегрирования а и b определенный интеграл (13) заведомо существует (представляет собой некоторое конечное число ). То есть при указанных условиях

- число. (18)

Р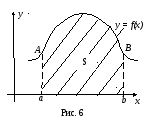авенство (18) будем считать математическим определением определенного интеграла. Определенным он называется потому, что в отличие от неопределенного интеграла , представляющего собой бесчисленное множество функций, он представляет собой вполне определенное число. Таким образом, несмотря на внешнее сходство в обозначениях определенного и неопределенного интегралов, это совершенно разные вещи. Впрочем, как это ни удивительно, между ними имеется связь. Но об этом мы поговорим несколько позже.

А сейчас подтвердим, что в случае непрерывной подынтегральной функции и конечных пределов интегрирования определенный интеграл (17) действительно представляет собой некоторое конечное число. Для этого рассмотрим все возможные случаи относительно функции .

а) Пусть непрерывная функция для всех . Тогда, согласно (4), определенный интеграл (17) можно представлять себе как площадь криволинейной трапеции (рис.6). И эта площадь S заведомо представляет собой число:

- число (19)

б) Пусть непрерывная функция для всех . Тогда функция для всех (см. рис. 5). В этом случае

(20)

То есть и в этом случае - число (только отрицательное). А именно, этот интеграл, как и в случае (а), представляет собой площадь криволинейной трапеции, заключенной между осью ох и графиком функции , только со знаком минус (рис. 8):

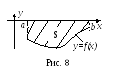
(21)

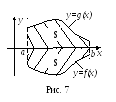
в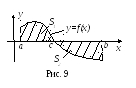) Наконец, если на части отрезка функция, а на другой части этого отрезка функция (рис 9), то

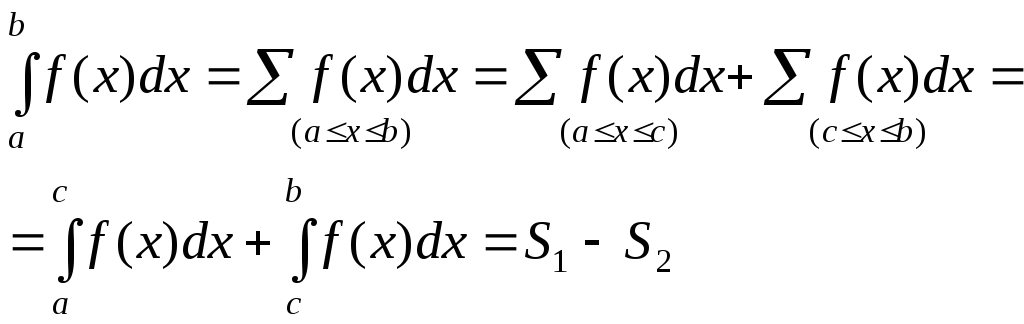То есть и в этом случае представляет собой число.

Итак, подтверждение получено: для любой непрерывной на конечном промежутке функции f(x) определенный интеграл существует (представляет собой некоторое число).

Заметим, что определенные интегралы рассматривают и для разрывных подынтегральных функций, а также тогда, когда пределы интегрирования бесконечные. В таких случаях определенные интегралы могут и не существовать. Об этих интегралах мы поговорим позднее.

Основные свойства определенных интегралов

Наиболее просто и естественно установить эти свойства, опираясь на какой-либо наглядный смысл определенного интеграла. Например, на то, что любой определенный интеграл связан, согласно (3), (5) и (6), с площадями криволинейных трапеций. Но использовать этот геометрический смысл определенного интеграла для вывода его свойств в самом общем случае, то есть в случае знакопеременной функции y = f(x), не очень удобно. Гораздо удобнее и нагляднее установить эти свойства, если, в соответствии с (12), считать определенный интеграл работой А силы f(x) (силы любого направления, а значит, и любого знака), когда точка приложения х этой силы перемещается вдоль оси ох из положения а в положение b (рис. 10).

(22)

Тогда сразу становятся очевидными следующие

Свойства определенных интегралов:

1) – число

(23)

(число А может быть любого знака).

2)

(24)

(переменную интегрирования в определенном интеграле можно обозначить как угодно – результат не изменится).

3)

(25)

(ибо если перемещение точки отсутствует, то работа любой силы f(x) равна нулю).

4)

(26)

(ибо если сила отсутствует, то и работа отсутствует).

5)

(27)

(ибо работа постоянной единичной силы численно равна перемещению точки под действием этой силы).

6)

(28)

7) Для любых трех чисел a,b и c ( при всех возможных их расположениях относительно друг друга, см рисунки ниже ) справедливо равенство

(29)

8) (30)

9)

(31)

10) Если f(x) ≤ g(x) для всех x[a; b], то

(32)

(физический смысл последних пяти свойств продумать самостоятельно).

11) Пусть m = [f(x)]_наим и М = [f(x)]_наиб – соответственно наименьшее и наибольшее значения функции f(x) на промежутке [a; b]. Тогда

(33)

Действительно, так как m ≤ f(x)≤ M для всех x [a; b], то применяя свойство (32) и затем свойства (31) и (27), мы и получим двойное неравенство (33). Это неравенство часто используется для прикидки (грубой оценки) величины .

12) ( теорема о среднем ). Если функция f(x) непрерывна на отрезке [a; b], то на этом отрезке найдется такая точка , что справедливо следующее равенство:

(34)

Пример 1. Оценить величину .

Решение. Так как функция монотонно возрастает на отрезке [1; 3], то Поэтому по формуле грубой оценки (33) получаем:

Пример 2. Оценить величину .

Решение. Минимальное m и максимальное M значения функции на промежутке [0; ] не очевидны, так как с возрастанием х в выражении x + cos x первое слагаемое растет, а второе убывает. Чтобы разобраться в поведении функции y, найдем ее производную:

.

Так как sin x ≤ 1 для всех х, то для всех х. А значит, функция убывает на всей области своего определения, в том числе и на отрезке [0; ]. Таким образом, на отрезке [0; ]

Следовательно, оценка (4.18) для данного интеграла имеет вид:

Вычисление определенных интегралов (приближенное и точное). Формула Ньютона-Лейбница

Определенный интеграл , согласно его математическому определению (18), представляет собой сумму бесконечно большого числа бесконечно малых слагаемых, образованных по схеме рисунка 5. Для непрерывной подынтегральной функции f(x) и конечных пределов интегрирования a и b этот интеграл, как было показано выше, заведомо существует (представляет собой некоторое число). Но найти его напрямую, следуя указанной на рис. 5 схеме, очевидно, невозможно. По этой схеме его можно найти лишь приближенно.

Для этого промежуток интегрирования [a; b] следует разбить не на бесконечно малые участки dx, которых будет бесконечно много, а на конечное число (скажем, на 100) частичных промежутков одинаковой (или не одинаковой) конечной длины . Затем на каждом выбрать некоторую точку х (скажем, середину) и подсчитать сумму

из уже конечного числа (из 100) слагаемых. Эта сумма будет приближенным значением определенного интеграла . Если нужно получить более точный результат, то нужно сделать более мелкое разбиение промежутка интегрирования (скажем, разбить его не на 100 частичных промежутков, а на 200, 300, и т. д.). Собственно, таким путем (с некоторыми непринципиальными усовершенствованиями указанной схемы) и вычисляют приближенно определенные интегралы на ЭВМ. ЭВМ умеют, кстати, оценивать точность полученного результата, и при вычислении определенных интегралов за счет своего быстродействия способны достигать любой разумной точности (до нескольких тысяч десятичных знаков после запятой). Но, вычисляя таким путем определенные интегралы, абсолютно точного результата, тем не менее, ЭВМ дать не в состоянии.

И тут возникает вопрос: а нельзя ли все-таки вычислять определенные интегралы абсолютно точно? Ответ на это вопрос такой: можно, хотя далеко и не всегда. Для точного подсчета определенных интегралов, если оно возможно, применяется знаменитая формула Ньютона-Лейбница.

Суть ее в следующем. Пусть f(x) – непрерывная на [a; b] функция, так что заведомо существует. И пусть вычислен неопределенный интеграл от функции f(x):

(35)

Тогда точное значение можно найти по формуле:

(36)

Здесь F(x) – любая первообразная для функции f(x). Формула (36) называется формулой Ньютона-Лейбница.

Для доказательства формулы Ньютона-Лейбница докажем сначала, что функция

(37)

то есть определенный интеграл с переменным верхним пределом, имеет на [a; b] производную Ф΄(x), совпадающую с f(x) (Ф΄(x) = f(x)).

Действительно,

(38)

Но

(39)

В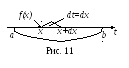 последнем интеграле интегрирование происходит на бесконечно малом промежутке [x; x+dx] оси t длиной dx. На нем, при его разбиении на бесконечно малые промежутки dt, уместится лишь один такой промежуток dt = dx (см.рис.11). Выбирая на нем в качестве произвольно выбираемой точки t точку x и следуя схеме (18) вычисления определенного интеграла, получим по этой схеме лишь одно слагаемое:

(40)

А значит, согласно (38), получаем:

(41)

Отметим, что заодно мы доказали следующий принципиальный факт: у любой непрерывной на [a; b] функции f(x) имеется первообразная F(x). Ею, в частности, является функция Ф(х). А значит, для любой непрерывной на [a; b] функции f(x) существует для x  [a; b] и неопределенный интеграл (35). Хотя, как мы уже замечали, он далеко не всегда может быть выражен через элементарные функции (может оказаться неберущимся). Найдя приближенно (машинным путем) функцию Ф(х), мы тем самым найдем приближенно и .

А теперь перейдем непосредственно к доказательству формулы Ньютона-Лейбница (36). Пусть F(x) – любая первообразная для функции f(x) на [a; b]. Так как она может отличаться от указанной выше первообразной Ф(х) лишь на константу, то

(42)

Полагая в этом равенстве х = а, получаем:

(43)

Значит, равенство (41) принимает вид:

(44)

А теперь, полагая в (44) х = b, получим:

(45)

Но это, по сути, это и есть формула (36) Ньютона-Лейбница.

Пример 3. Вычислить .

Решение. Вычислим сначала

(значит, )

А тогда

(46)

Геометрическая иллюстрация полученного результата изображена ниже:

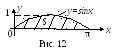
Формула Ньютона-Лейбница (36) принадлежит к числу важнейших формул высшей математики. Она позволяет просто, а главное, точно вычислять определенные интегралы. А значит, позволяет находить точные значения многих нужных для практики величин (площадей криволинейных фигур; помещений тел при переменных скоростях их движения; работ переменных сил и многое другое). Но она может быть использована, если только соответствующий неопределенный интеграл – из берущихся. В противном случае неизвестна первообразная F(x) для функции f(x), а значит, нечего подставлять и в формулу (36) Ньютона-Лейбница.

Если неопределенный интеграл неберущийся, то соответствующий ему определенный интеграл может быть найден лишь приближенно. Например, с помощью ЭВМ – так, как об этом говорилось выше, перед выводом формулы Ньютона-Лейбница.