
Лекция 25. Некоторые теоремы о дифференцируемых функциях. Правило Лопиталя. Производные высших порядков. Формула Тейлора. Разложение функций по формуле Тейлора.
Некоторые теоремы о дифференцируемых функциях.
Теорема Ролля: ( теорема о корнях производной )
Если функция f(x)
непрерывна на отрезке
![]() ,
дифференцируема во всех внутренних
точках этого отрезка и на концах x=a
и x=b
обращается в нуль f(a)=f(b)=0,
то существует внутри отрезка
,
дифференцируема во всех внутренних
точках этого отрезка и на концах x=a
и x=b
обращается в нуль f(a)=f(b)=0,
то существует внутри отрезка
![]() по крайней мере одна точка x=с,
a<c<b
, в которой
производной
по крайней мере одна точка x=с,
a<c<b
, в которой
производной
![]() обращается в нуль, т.е.
обращается в нуль, т.е.
![]() .
.
( см. рис.1 )
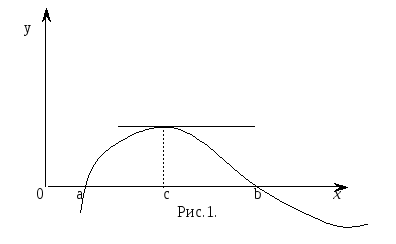
Геометрическое
истолкование:
если непрерывная кривая, имеющая в
каждой точке касательную, пересекает
ось Ох
в точках с абсциссами a
и b,
то на этой кривой найдется по крайней
мере одна точка с абсциссой с,
![]() ,
в которой касательная параллельна оси
Ох.
,
в которой касательная параллельна оси
Ох.
Теорема Лагранжа: ( теорема о конечных приложениях )
Если функция f(x)
непрерывна на отрезке
![]() ,
дифференцируема во всех внутренних
точках этого отрезка, то внутри отрезка
,
дифференцируема во всех внутренних
точках этого отрезка, то внутри отрезка
![]() найдется по крайней мере одна точка с,
a<c<b,
что
найдется по крайней мере одна точка с,
a<c<b,
что
![]() .
( см. рис.2 )
.
( см. рис.2 )
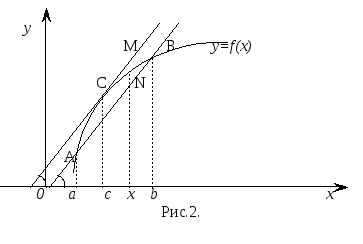
Геометрическое истолкование: если во всех точках дуги AB существует касательная, то на этой дуге найдется точка С между A и B, в которой касательная параллельна хорде, соединяющей точки A и B.
Теорема Коши: ( теорема об отношении приращений двух функций )
Если f(x)
и
![]() - две функции, непрерывные на отрезке
- две функции, непрерывные на отрезке
![]() и дифференцируемых внутри него, причем
и дифференцируемых внутри него, причем
![]() нигде внутри отрезка не обращается в
нуль, то внутри отрезка
нигде внутри отрезка не обращается в
нуль, то внутри отрезка
![]() найдется по крайней мере одна точка с,
a<c<b,
что
найдется по крайней мере одна точка с,
a<c<b,
что
![]() .
.
Производные высших порядков.
Пусть
![]() – некоторая заданная функция, а
– некоторая заданная функция, а
![]() – ее производная. Тогда
– ее производная. Тогда
![]() – производная
второго порядка
от функции y.
Применяют и другие обозначения этой
производной:
– производная
второго порядка
от функции y.
Применяют и другие обозначения этой
производной:
![]() (1)
(1)
Далее,
![]() (2)
(2)
– производная
третьего порядка
от функции y.
И т.д. Кстати, обычную производную
![]() часто называют производной
первого порядка.
часто называют производной
первого порядка.
Пример 1.
![]() ;
;
![]()
Решение.
Сначала найдем
![]() и
и
![]() ,
а затем найдем и
,
а затем найдем и
![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Пример 2.
Функция
![]() задана неявно уравнением
задана неявно уравнением
![]() .
Найти
.
Найти
![]() .
.
Решение.
Сначала найдем
![]() :
:
![]() .
.
Теперь найдем и
![]() :
:
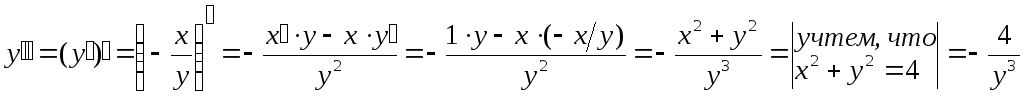
Пример 3.
Функция
![]() задана параметрически:
задана параметрически:
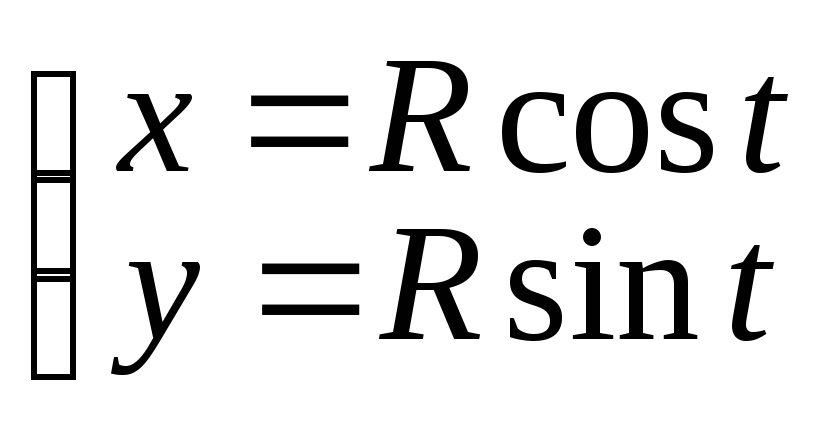
Найти
![]() .
.
Решение.
Сначала найдем
![]() :
:
![]() .
А теперь найдем
.
А теперь найдем
![]() :
:
![]() .
.
Физический смысл производной второго порядка.
Если
![]() – уравнение движения точки по ее
траектории, то, как мы знаем, ее производная
– уравнение движения точки по ее
траектории, то, как мы знаем, ее производная
![]() (производная первого порядка) представляет
собой скорость v(x)
движения точки (мгновенную скорость
движения) . Но тогда производная второго
порядка
(производная первого порядка) представляет
собой скорость v(x)
движения точки (мгновенную скорость
движения) . Но тогда производная второго
порядка
![]() будет иметь смысл «скорость изменения
скорости» движения точки. В физике такая
величина называется ускорением. Поэтому
будет иметь смысл «скорость изменения
скорости» движения точки. В физике такая
величина называется ускорением. Поэтому
![]() (3)
(3)
– ускорение движения точки в момент x. В этом и состоит физический смысл производной второго порядка.
Пример 4.
Как известно, уравнение движения свободно
падающего в безвоздушном пространстве
тела, начавшего свое падение в момент
![]() ,
имеет вид:
,
имеет вид:
![]() (s
– путь, пройденный падающим телом за
время t).
Найдем скорость
(s
– путь, пройденный падающим телом за
время t).
Найдем скорость
![]() и ускорение
и ускорение
![]() падающего тела:
падающего тела:
![]() ;
;
![]() .
.
То есть ускорение
a
падающего тела неизменно и равно g
– ускорению свободного падения (![]() м/сек2).
А скорость v
падающего тела возрастает пропорционально
времени по формуле
м/сек2).
А скорость v
падающего тела возрастает пропорционально
времени по формуле
![]() .
.
Упражнения
-
Найти угол наклона к оси ох касательной, проведенной к параболе
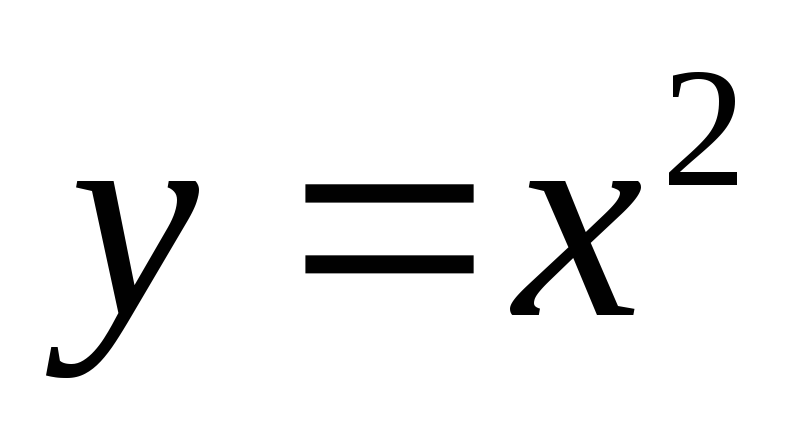 в точке
в точке
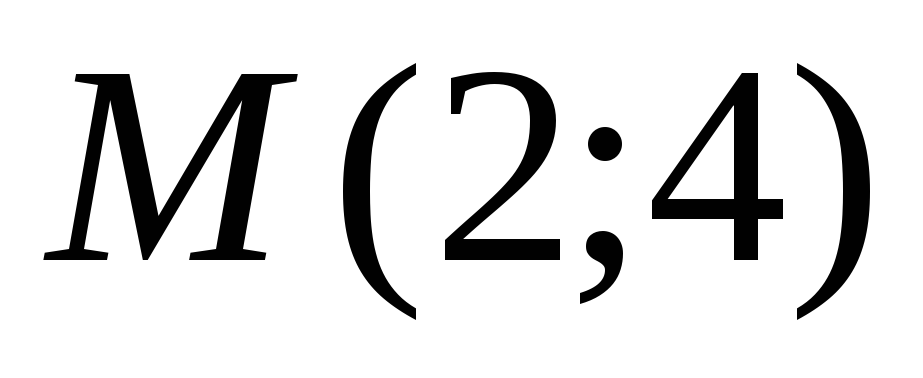 .
.
Ответ:
![]() .
.
-
Найти на параболе
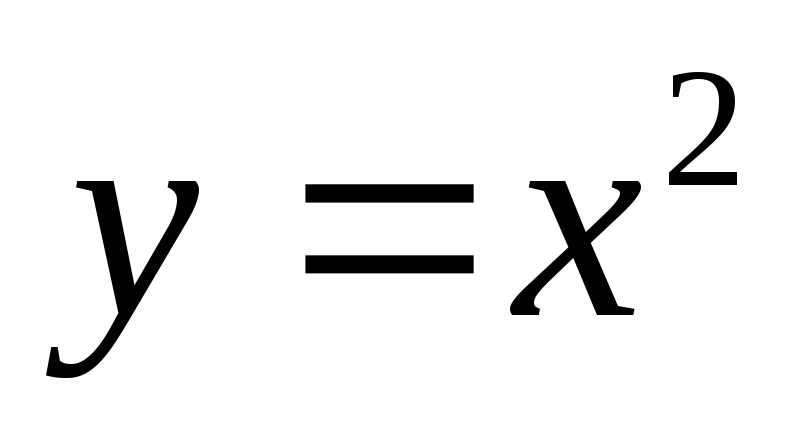 такую точку
такую точку
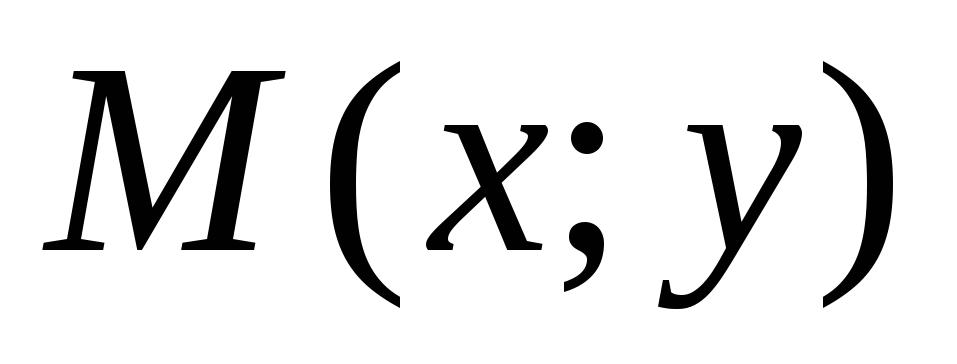 ,
чтобы касательная к параболе, проведенная
в этой точке, составила с осью ох
угол
,
чтобы касательная к параболе, проведенная
в этой точке, составила с осью ох
угол
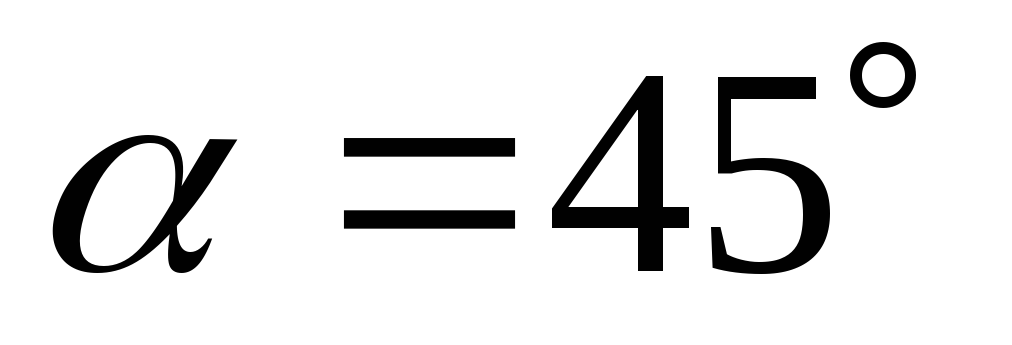 .
.
Ответ:
![]() .
.
-
В момент времени
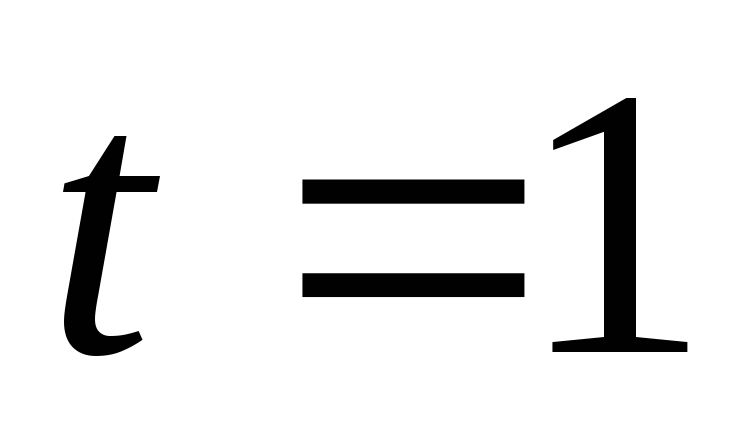 найти скорость v
и ускорение a
точки, движущейся по оси ох
по закону
найти скорость v
и ускорение a
точки, движущейся по оси ох
по закону
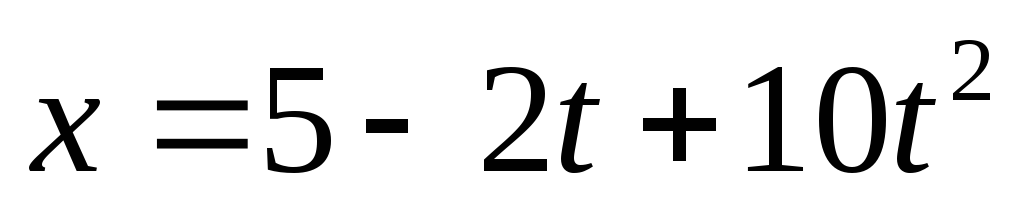 .
.
Ответ:
![]() ;
;
![]() .
.
-
Найти производную
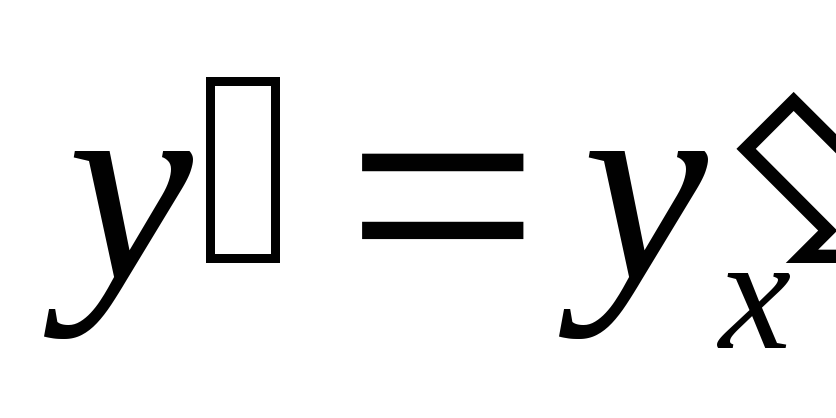 функций:
функций:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
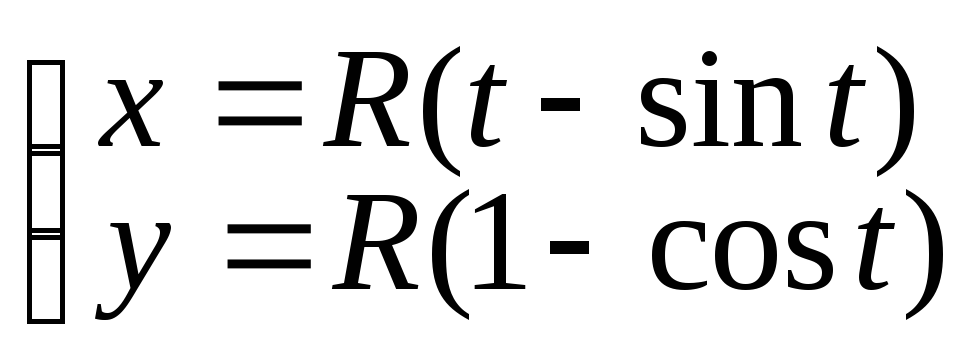
Ответ:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() .
.
-
Найти производную
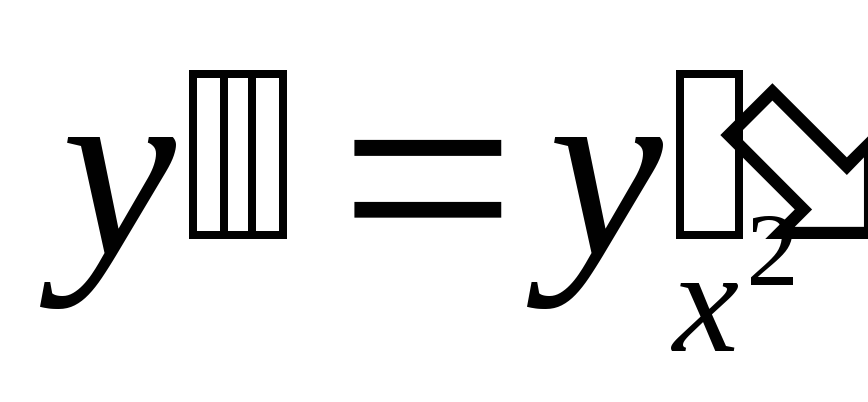 функций:
функций:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
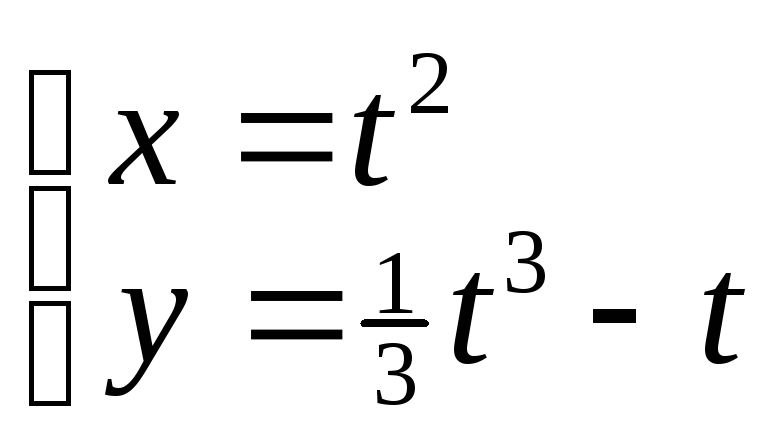 .
.
Ответ:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
Правило Лопиталя вычисления пределов.
Это правило состоит в следующем. Если требуется найти предел вида
![]() ,
(4)
,
(4)
где x0
– число или символ
![]() ,
и этот предел приводит к неопределенности
вида
,
и этот предел приводит к неопределенности
вида
![]() или
или
![]() ,
то
,
то
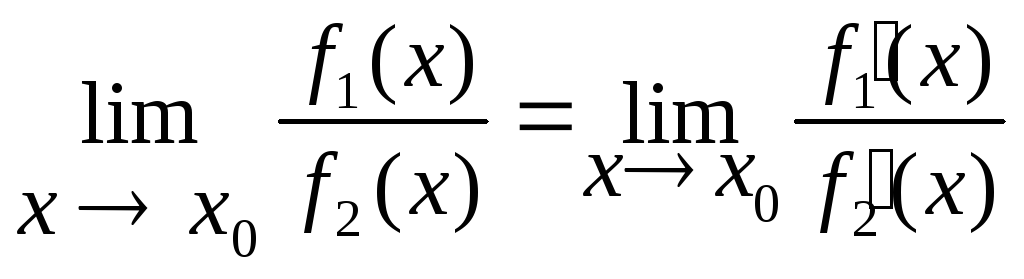 ,
(5)
,
(5)
Словесная формулировка правила Лопиталя (5) такова: предел отношения бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует.
Доказательство.
Исчерпывающее доказательство правила
Лопиталя довольно громоздко. В связи с
этим ограничимся рассмотрением случая,
когда предел (4) приводит к неопределенности
вида
![]() :
:
![]() ;
;
![]() ;
;
![]() .
(6)
.
(6)
При этом будем считать, что x0 – некоторое конечное число.
Если функции
![]() и
и
![]() непрерывны в точке x0,
то в силу определения непрерывности
функций верны следующие равенства
непрерывны в точке x0,
то в силу определения непрерывности
функций верны следующие равенства
![]() и
и
![]() .
Если же эти функции в точке x0
разрывны,
то их значения при x0
не равны нулю (у них другие значения или
они там вообще не определены). Тогда
переопределим (или доопределим) их в
точке x0
так, чтобы стало
.
Если же эти функции в точке x0
разрывны,
то их значения при x0
не равны нулю (у них другие значения или
они там вообще не определены). Тогда
переопределим (или доопределим) их в
точке x0
так, чтобы стало
![]() и
и
![]() .
После этого, в силу того же определения
непрерывности функций, функции
.
После этого, в силу того же определения
непрерывности функций, функции
![]() и
и
![]() станут непрерывными в точке x0.
Далее, будем считать, что обе эти функции
будут непрерывно дифференцируемыми в
окрестности точки х0,
включая саму точку
х0,
причем
станут непрерывными в точке x0.
Далее, будем считать, что обе эти функции
будут непрерывно дифференцируемыми в
окрестности точки х0,
включая саму точку
х0,
причем
![]() .
Тогда получим:
.
Тогда получим:
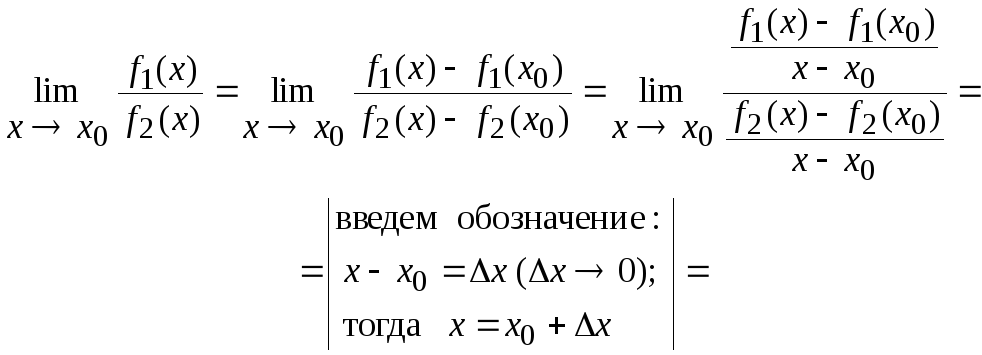
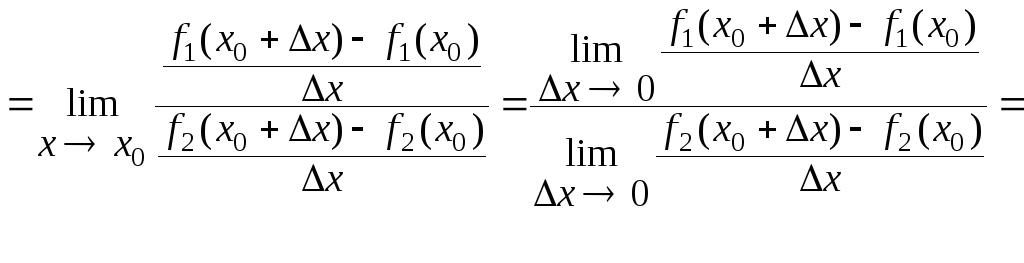
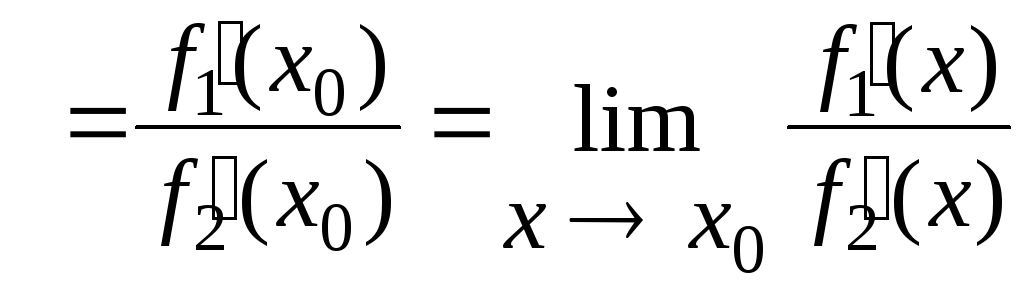
Примечание.
Предел отношения производных, стоящий
в правой части равенства (5), тоже может
приводить к неопределенности вида
![]() или
или
![]() .
Тогда правило Лопиталя можно применить
и к нему. То есть применить это правило
повторно.
.
Тогда правило Лопиталя можно применить
и к нему. То есть применить это правило
повторно.
Пример 5.
![]() .
.
Пример 6.
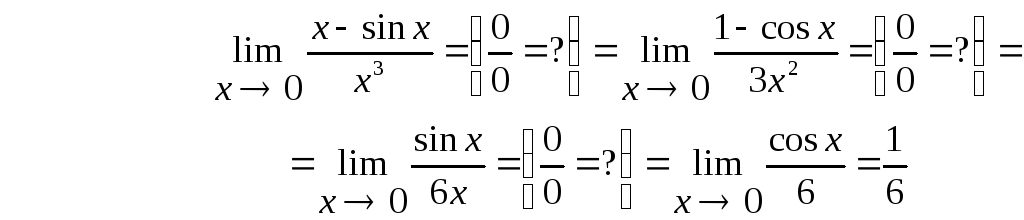
Пример 7.
![]() .
.
Пример 8.
![]()
![]() .
.
Последние два
примера показывают, что при
![]()
![]() растет несравненно медленнее, чем x,
а
растет несравненно медленнее, чем x,
а
![]() – несравненно быстрее, чем
– несравненно быстрее, чем
![]() при любом значении n.
при любом значении n.
Пример 9.
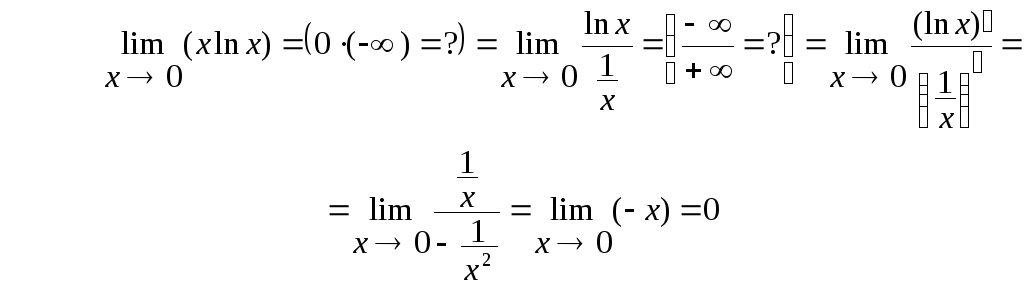
Пример 10.
![]() .
.
Для вычисления
этого предела введем обозначение:
![]() .
Тогда
.
Тогда
![]() .
Учитывая, что
.
Учитывая, что
![]() ,
находим:
,
находим:
![]()
Итак,
![]() .
То есть при
.
То есть при
![]() и
и
![]() ,
а значит,
,
а значит,
![]() ,
ибо
,
ибо
![]() .
Таким образом,
.
Таким образом,
![]() ,
а значит,
,
а значит,
![]() .
.
Упражнения
-
С помощью правила Лопиталя найти пределы:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() .
.
Ответ:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г) 2; д)
;
г) 2; д)
![]() .
.
-
С помощью правила Лопиталя доказать второй замечательный предел:
![]() .
.
-
С помощью правила Лопиталя доказать, что при
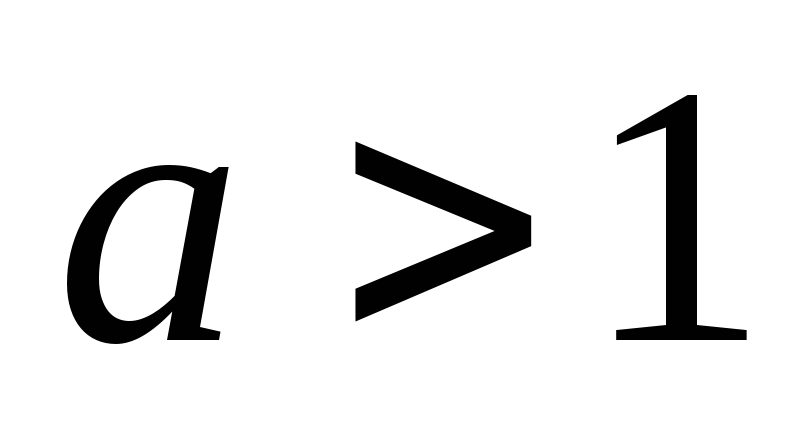 и любом n
и любом n
![]() .
.
Дифференциалы высших порядков.
Найдя дифференциал
dy
данной функции
![]() ,
можем затем найти дифференциал от этого
дифференциала. Тем самым получим так
называемый дифференциал
второго порядка
,
можем затем найти дифференциал от этого
дифференциала. Тем самым получим так
называемый дифференциал
второго порядка
![]() данной функции
данной функции
![]() :
:
![]()
![]() .
.
Итак, если
![]() – некоторая дважды дифференцируемая
функция, то ее дифференциал второго
порядка
– некоторая дважды дифференцируемая
функция, то ее дифференциал второго
порядка
![]() (дэ два игрек) находится по формуле:
(дэ два игрек) находится по формуле:
![]() (7)
(7)
Отсюда, кстати, получаем:
![]() ,
где
,
где
![]() (8)
(8)
Тем самым находит
свое оправдание обозначение Лейбница
(1) для производной второго порядка
функции
![]() .
Аналогично получает оправдание и
обозначение (2) для производной третьего
порядка, которая выражается через
дифференциал
.
Аналогично получает оправдание и
обозначение (2) для производной третьего
порядка, которая выражается через
дифференциал
![]() (дэ три игрек) третьего порядка
(дэ три игрек) третьего порядка
![]() ,
откуда
,
откуда
![]() ,
(9)
,
(9)
и т.д.
Отметим еще одно
существенное обстоятельство. Дифференциал
dy
функции y
(дифференциал первого порядка), как
показано выше, имеет инвариантную
(неизменную) форму
![]() независимо от того, является ли аргумент
x
функции y
независимой переменной или, наоборот,
сам является функцией от другой
переменной. А вот для дифференциалов
высших порядков (
независимо от того, является ли аргумент
x
функции y
независимой переменной или, наоборот,
сам является функцией от другой
переменной. А вот для дифференциалов
высших порядков (![]() ,
,
![]() ,
…) эта
инвариантность места не имеет.
,
…) эта
инвариантность места не имеет.
Действительно,
пусть
![]() – сложная функция от t.
Тогда, согласно инвариантности формы
первого дифференциала dy,
имеем:
– сложная функция от t.
Тогда, согласно инвариантности формы
первого дифференциала dy,
имеем:
![]() .
.
А вот
![]() (10)
(10)
Действительно,
![]()
![]()
