3. Задание на работу

Задача 1. Сколько костей должна содержать игра в домино, если бы наибольшее число очков на кости было равно ?

Варианты

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

Задача 2. Найти натуральные корни уравнения.

Варианты

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

Задача 3. Окрашенный куб с ребром 10 см распиливается на кубики с ребром 1 см. Сколькими способами из этих кубиков можно взять кубиков, среди которых кубиков имеют 3 окрашенных грани, кубиков имеют 2 окрашенных грани кубиков имеют 1 окрашенную грань, кубиков не имеют ни одной окрашенной грани.

Варианты

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

10. 

11. 

12. 

13. 

14. 

15. 

Задача 4. Слово некоторого гипотетического языка разрезается на буквы. Затем путем перестановки букв составляются другие слова. Сколько таких слов можно составить? (Считается, что любой набор букв дает некоторое слово языка.)

Варианты

1. ШИРЛИЛИРЛИ

2. МУСИПУСИ

3. АВВАГАВВА

4. МУМБАЮМБА

5. АЛКАКАЛКА

6. ЕЛКИПАЛКИ

7. АБРАКАДАБРА

8. ТОРОТОРО

9. РОНГОРАНГА

10. КУКАРЕКУКУ

11. РОНГОРОНГО

12. КУРКАУРКА

13. ВИЛКАПИЛКА

14. ЧУЧАЧАЛЛА

15. КАРАКАЧЧА

Образец выполнения работы

Задача 1. Сколько костей должна содержать игра в домино, если бы наибольшее число очков на кости было равно ?

Решение. Кость с максимальным числом очков – это дубль . Все кости разбиваем на несколько классов. Вот эти классы. всего 11 костей,

всего 10 костей,

всего 9 костей. И так далее... Последний класс содержит всего одну кость: . Находим сумму костей . Ответ: 66.

Задача 2. Найти натуральные корни уравнения .

Решение. Согласно одному из свойств сочетаний , поэтому исходное уравнение примет вид: . Преобразуем уравнение по формулам (1) и (3):

Корень не удовлетворяет условию задачи. Ответ: 6.

Задача 3. Окрашенный куб с ребром 10 см распиливается на кубики с ребром 1 см. Сколькими способами из этих кубиков можно взять 11 кубиков, среди которых 4 кубика имеют три окрашенных грани, 3 кубика имеют две окрашенных грани, 2 кубика имеют одну окрашенную грань, 2 кубика не имеют ни одной окрашенной грани.

Р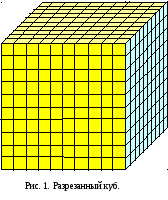ешение. Исходный куб распиливается на кубиков с ребром в 1 см (см. рис. 1). Кубики с 3 окрашенными гранями находились в вершинах исходного куба, поэтому их будет 8 штук. Кубики с 2 окрашенными гранями находились на ребрах исходного куба за исключением двух граничных, у которых по три окрашенных грани (см. рис. 1). Поэтому на каждом ребре будет по 8 таких кубиков. Общее количество кубиков с 2 окрашенными гранями равно . Кубики с 1 окра-шенной гранью находились на гранях исходного куба за исключением ребер, где у кубиков по две или три окрашенных грани (см. рис. 1). Общее количество кубиков с 1 окрашенной гранью равно . Кубики с неокрашенными гранями находились внутри исходного куба, поэтому их общее количество равно . Проверим правильность расчетов. Сложим найденные количества кубиков с разным числом окрашенных граней: ; общее число кубиков совпало с подсчитанным ранее другим способом.

Кубики с тремя окрашенными гранями отбираются из 8 кубиков. Поскольку порядок отбора кубиков не важен, речь идет о сочетаниях. Поэтому 4 кубика с тремя окрашенными гранями можно отобрать способами. Кубики с двумя окрашенными гранями отбираются из 96 кубиков. Порядок отбора кубиков опять не важен, поэтому речь снова идет о сочетаниях. Значит, 3 кубика с двумя окрашенными гранями можно отобрать способами. Аналогично 2 кубика с одной окрашенной можно отобрать способами, 2 кубика с одной окрашенной можно отобрать способами. Теперь по правилу произведения число способов отбора 4 кубика с тремя окрашенными гранями, 3 кубика с двумя окрашенными гранями, 2 кубика с одной окрашенной гранью, 2 кубика с неокрашенными гранями равно .

Число сочетаний находим по формуле (3). Получим

Таким образом,

Ответ:

Задача 4. Слово ШИШКАМИШКА некоторого гипотетического языка разрезается на буквы. Затем путем перестановки букв составляются другие слова. Сколько таких слов можно составить? (Считается, что любой набор букв дает некоторое слово языка.)

Решение. Любое новое слово – это перестановка букв, причем, некоторые слова будут повторяться. То есть речь идет о перестановках с повторениями. Буквы слова ШИШКАМИШКА образуют пять групп:

Ш,Ш,Ш, И,И, К,К, А,А, М. Значит, . Число слов находим по формуле (7).