10

Практическая работа 5: статистическая обработка выборочных данных Краткие сведения из теории

Генеральная совокупность – это множество всех значений, которые может принять изучаемая случайная величина при данном комплексе условий. Выборочная совокупность (или просто выборка) – это множество значений, случайным образом отобранных из генеральной совокупности. Значения, входящие в выборку, называются выборочными данными или вариантами. Выборочные данные будем обозначать: Количество выборочных данных, содержащихся в выборке, называется объемом выборки. Объем выборки в дальнейшем будем обозначать буквой .

Если выборочные данные расположить в возрастающем (точнее, в неубывающем) порядке, то такая последовательность выборочных данных называется вариационным рядом. Разность между максимальным и минимальным выборочными данными называется размахом выборки. Ясно, что размах выборки находится по формуле .

Если объем выборки велик, то проводят группировку выборочных данных. Для этого промежуток делят на равных частей точками . Обычно величину берут небольшой: . Затем считают количество попаданий выборочных данных в каждый из промежутков ; эти количества называются частотами (абсолютными частотами) попадания в интервалы и обозначаются . В итоге на основе выборочных данных получается таблица.

Интервалы				. . .
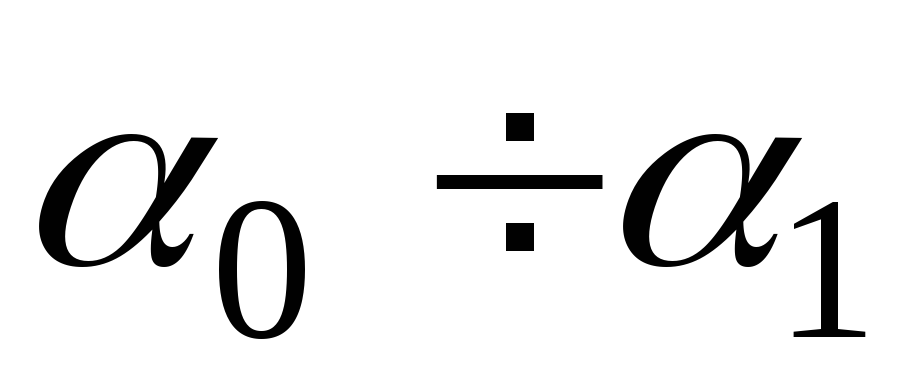
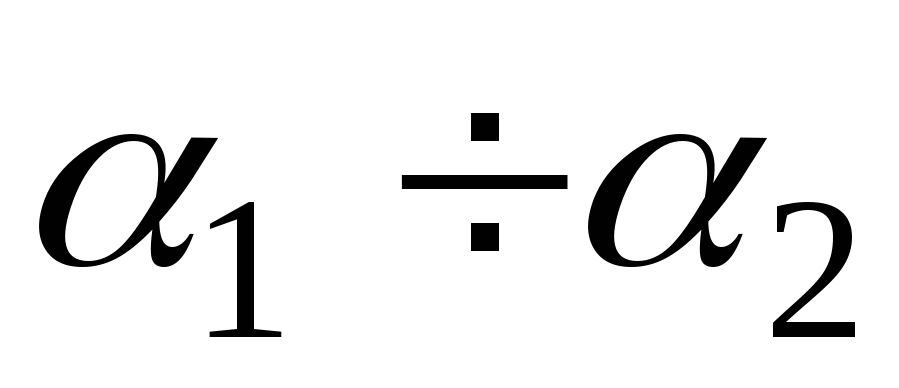
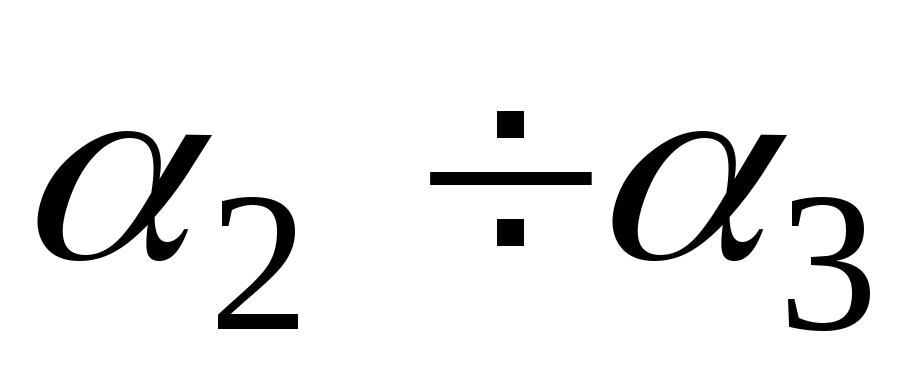
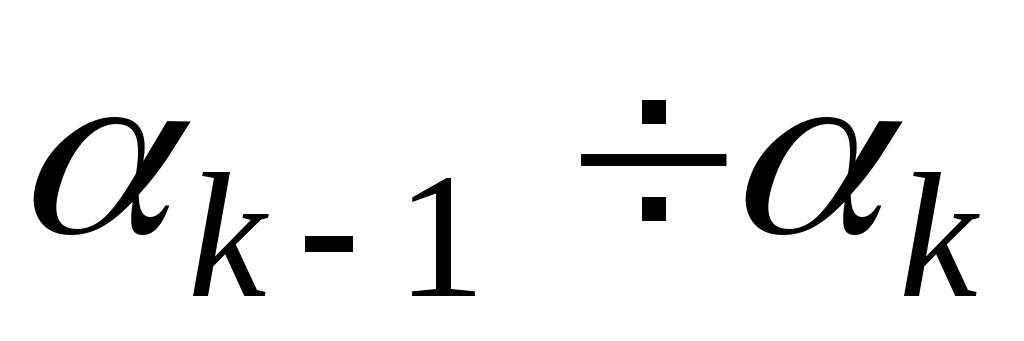
Частоты				. . .

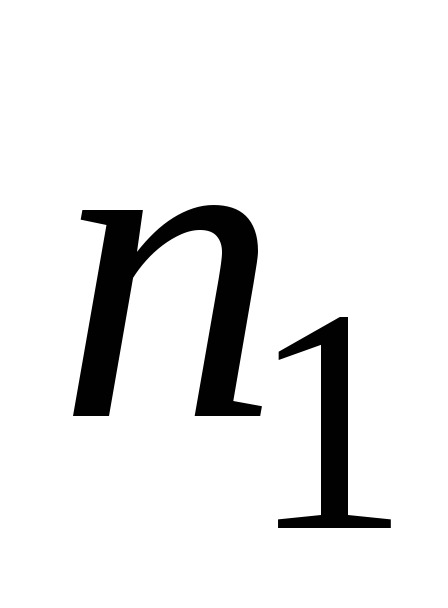
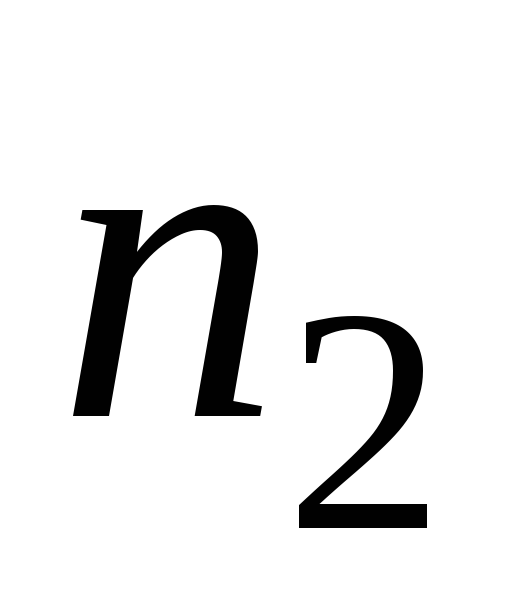
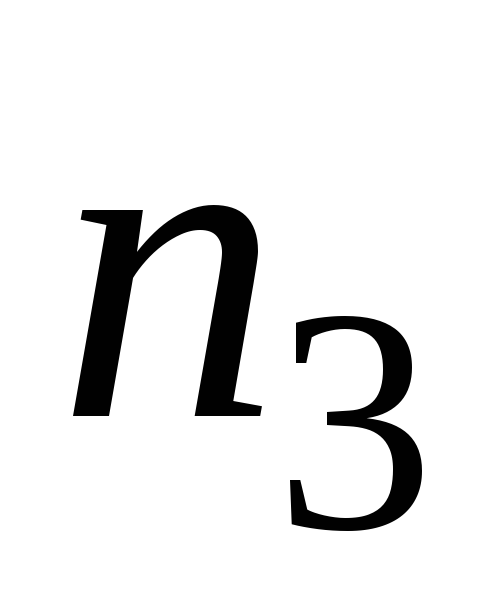
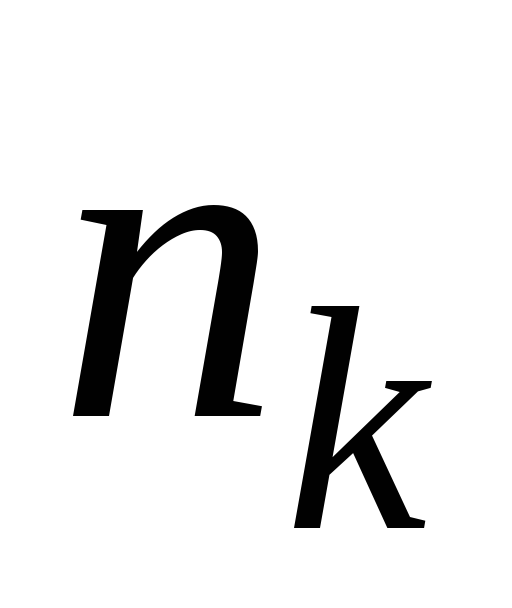
Эта таблица называется интервальным статистическим рядом. Числа называются частотами (точнее, абсолютными частотами).

Интервальный статистический ряд изображается графически в виде гистограммы (точнее, гистограммы абсолютных частот). Для этого на оси абсцисс откладываются отрезки . Над этими отрезками надстраиваются прямоугольники с высотами

Получающаяся при этом ступенчатая фигура и называется гистограммой (гистограммой абсолютных частот).

Для решения некоторых задач удобно от интервального статистического ряда перейти к группированному статистическому ряду. Для этого найдем середины интервалов интервального статистического ряда по формулам

и эти числа занесем в первую строку таблицы. Во вторую строку таблицы занесем частоты, взятые из интервального статистического ряда. В итоге получим следующую таблицу.

				. . .
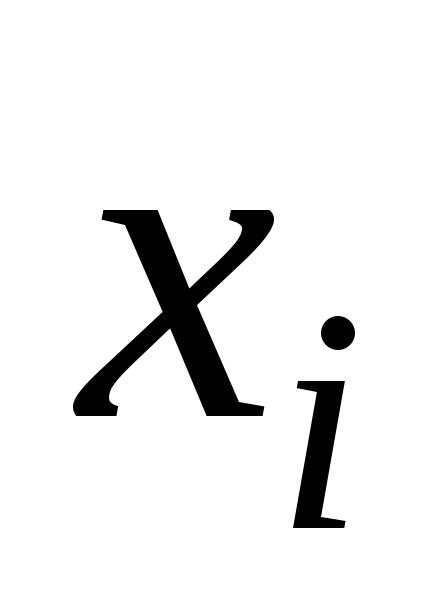
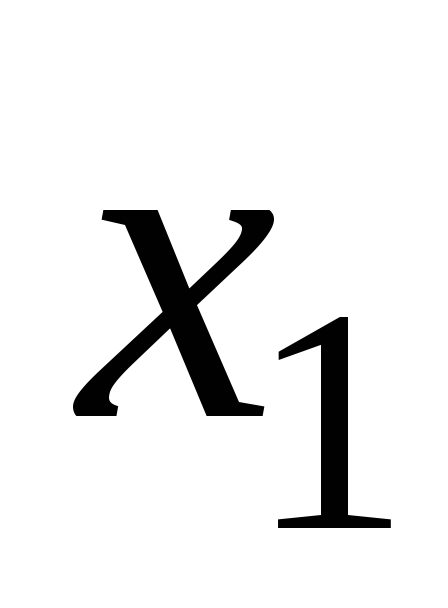
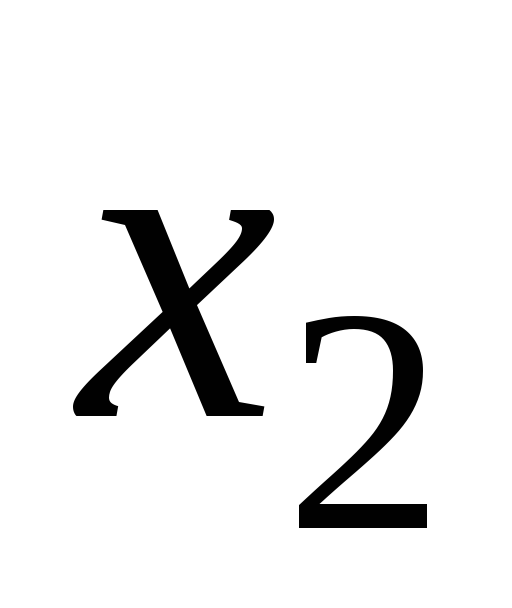
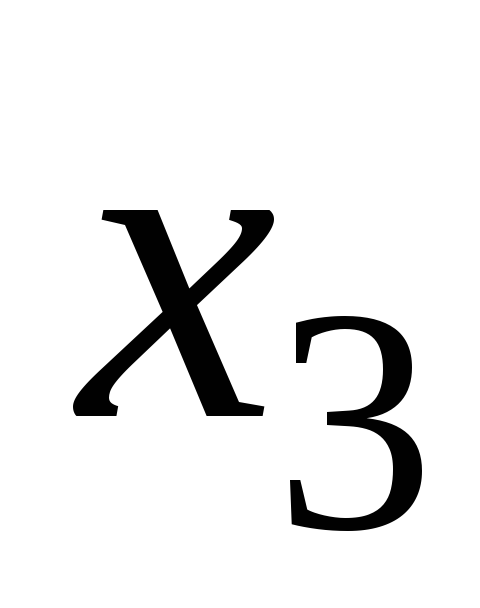
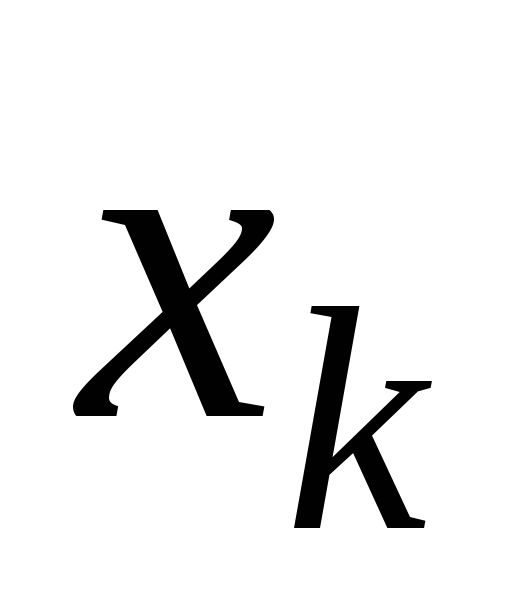
Частоты				. . .

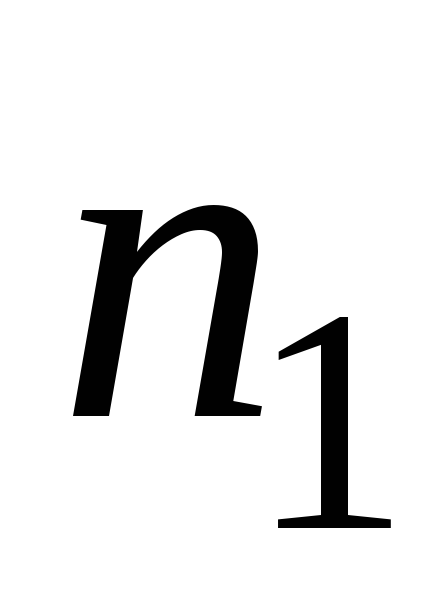
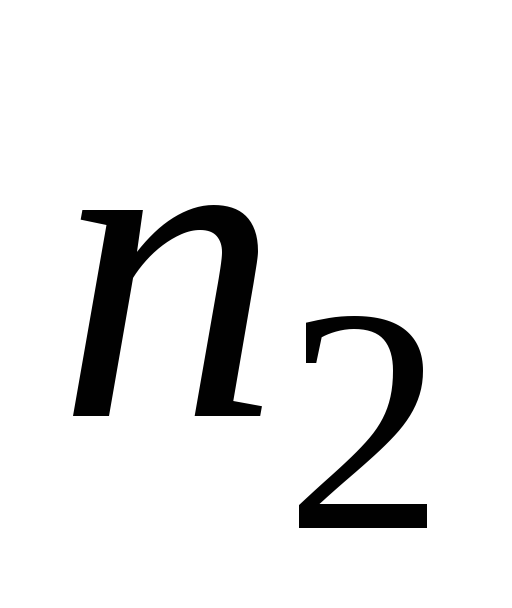
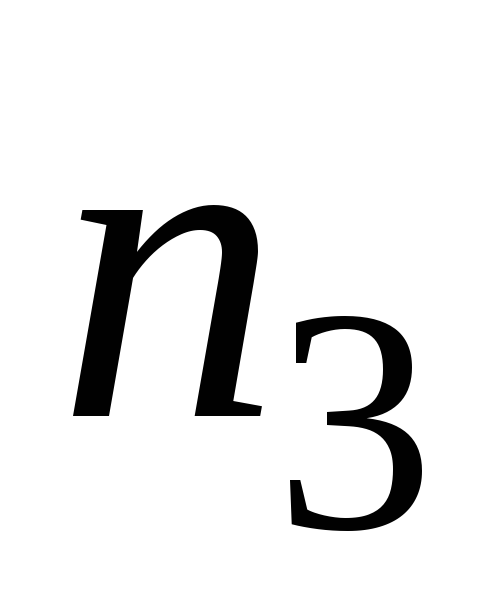
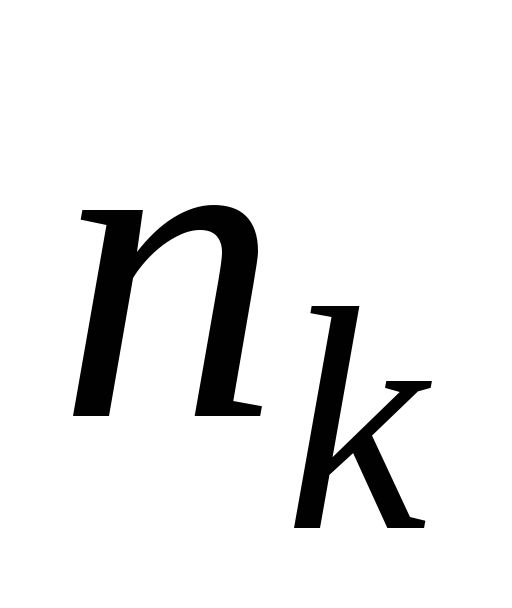
Эта таблица называется группированным статистическим рядом.

Группированным статистический ряд изображается графически в виде полигона. Для этого на оси абсцисс откладываются точки . Над этими точками надстраиваем перпендикуляры высотой . Концы перпендикуляров соединяем ломаной; эта ломаная и называется полигоном (точнее, полигоном абсолютных частот).

По группированному статистическому ряду можно построить эмпирическую функцию распределения по формуле

(1) в которой объем выборки, количество выборочных данных, меньших .

Приближенные значения параметров генеральной совокупности, вычисленные на основе статистических данных, называются статистическими оценками этих параметров. В качестве статистической оценки математического ожидания обычно берется выборочная средняя , которая находится по формуле

. (2)

В этой формуле объем выборки, варианты из группированного статистического ряда (данные из первой строки), их частоты.

В качестве статистической оценки дисперсии обычно берут исправленную выборочную дисперсию , которая находится так. Сначала находят по формуле (2) и по формуле

. (3)

Затем находят по формуле

. (4)

В качестве статистической оценки среднего квадратического отклонения берут исправленное выборочное среднее квадратическое отклонение , которое находится по формуле

. (5)

Важными характеристиками выборки является коэффициент вариации, мода и медиана. Коэффициент вариации находится по формуле

(6)

Мода это варианта статистического ряда, которая имеет наибольшую частоту. Медиана это варианта статистического ряда, которая делит статистический ряд пополам.

По виду гистограммы или полигона можно выбрать тип распределения генеральной совокупности. Для этого в случае гистограммы нужно построить гладкую кривую, огибающую гистограмму; в случае полигона – заменить полигон гладкой кривой. Из стандартных законов распределения (мы будем использовать нормальный, равномерный, показательный, Релея законы) нужно выбрать тот, у которого график плотности распределения больше всего напоминает полученную кривую. Этот закон нужно выбрать в качестве гипотезы о типе распределения генеральной совокупности. Затем на основе статистических данных нужно найти параметры выбранного закона. В результате мы получим приближенный вид закона распределения изучаемой генеральной совокупности; этот закон называется теоретическим распределением генеральной совокупности.

Затем следует проверить, насколько хорошо полученное теоретическое распределение соответствует статистическим данным. Для этого находим вероятности попадания теоретического распределения в интервалы интервального статистического ряда и на их основе теоретические частоты попадания в эти же интервалы. Разумеется, теоретические частоты будут в большей или меньшей степени отличаться от соответствующих экспериментальных частот . Близость частот и свидетельствует в пользу выбранной гипотезы, заметные различия требуют отвергнуть гипотезу.

В качестве меры рассогласования эмпирических и теоретических частот выступает критерий (статистика) (хи-квадрат), наблюдаемые значения которого находятся по формуле

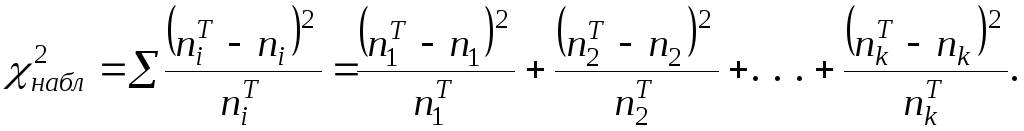(7)

Критерий (7) называется критерием Пирсона. Этот критерий распределен по закону Пирсона с параметром . При этом число групп (столбцов) в статистическом ряде, число параметров теоретического распределения, найденных на основе статистического ряда. В учебниках по математической статистике приводится таблица критических точек распределения Пирсона в зависимости от уровня значимости и параметра .

Фрагмент такой таблицы приведен ниже.

Таблица. Критические точки распределения Пирсона.

	Уровень значимости
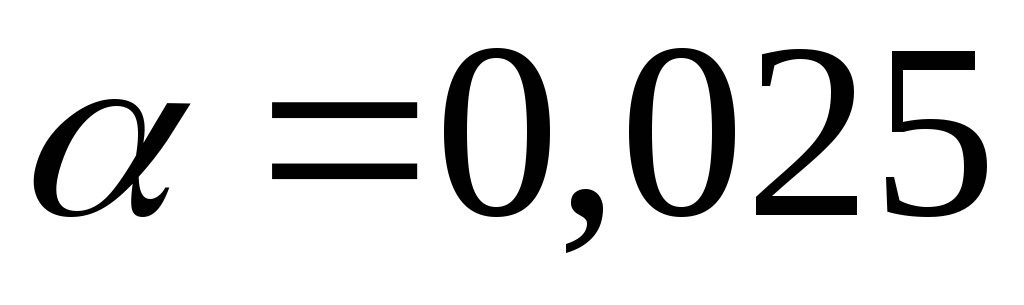
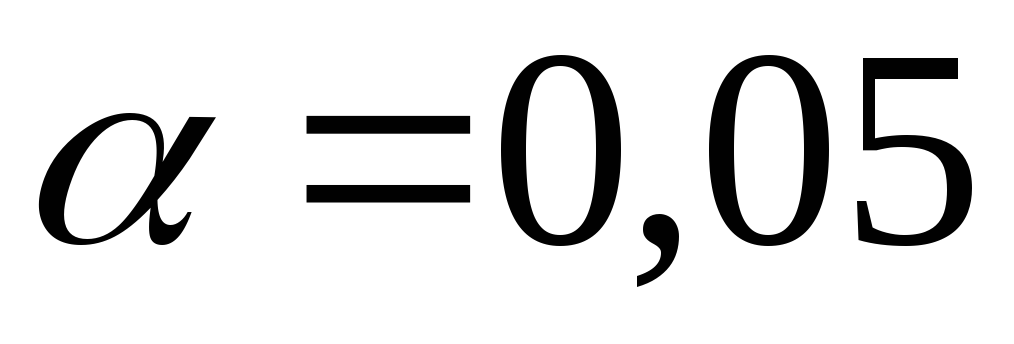
3 4 5 6 7 8 9 10	11,3 13,3 15,1 16,8 18,5 20,1 21,7 23,2	9,4 11,1 12,4 14,4 16,0 17,5 19,0 20,5	7,8 9,5 11,1 12,6 14,1 15,5 16,9 18,3

Зная величины и , мы с помощью этой таблицы можем найти критическое значение критерия Пирсона. Затем сравниваем значения и . Если , то исходная гипотеза о типе распределения принимается. Если же , то исходная гипотеза отвергается.