25

Практическая работа 4: элементы теории вероятностей

1. Краткие сведения из теории

Опр. 1. Произведением событий и называется новое собы­тие, состоящие в одновременном появлении событий и . Аналогично произведением n событий называется новое событие, состоящие в одновременном появлении всех событий .

Опр. 2. Суммой событий и называется новое событие, состоящее в появлении или , или , или в их одновременном появ­лении. Аналогично суммой событий называется новое событие, состоящие в появлении хотя бы одного из событий .

Опр. 3. Событие , состоящие в непоявлении события , называ­ется противоположным к .

Опр. 4. Говорят, что событие является следствием события , если при появлении события появляется событие .

Опр. 5. События и называются несовместными, если они не могут произойти одновременно. Ясно, что события и несовместны тогда и только тогда, когда Ø.

Опр. 6. События называются попарно несовместными, если любые два события из этой группы не могут происходить одновре-менно.

Предположим, что результатом эксперимента (опыта) являются равновозможных элементарных исходов. При этом исходы считаются равновозможными, если они имеют одина­ковую возможность появиться в результате эксперимента. Предполо­жим, что событию благоприятствуют k исходов. (Вспомните: исход называется благоприятствующим событию , если при его появлении появляется и событие .) Тогда вероятность события можно определить так.

Опр. 7. Вероятностью события называется отношение числа благоприятствующих исходов к общему числу исходов

. (1)

В этой формуле общее число исходов, число исходов, благопри-ятствующих событию . Введенная по формуле (1) вероятность называется классической вероятностью события .

Для решения многих задач по теории вероятностей нужно использовать теоремы о вероятности суммы и произведения событий.

Теорема 1. Вероятность суммы двух событий равна сумме их веро­ятностей минус вероятность их произведения .

Следствие. Вероятность суммы несовместных событий равна сумме их вероятностей, т. е. .

Теорема 2. Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого

Следствие. Вероятность произведения событий находится по формуле

.

Опр. 8. Говорят, что события А и В независимы, если вероят­ность появления одного из них не зависит от появления другого, т.е.

Опр. 9. Говорят, что события независимы в со­вокупности, если вероятности появления любого из них не зависит от появления остальных.

Теорема 3. Вероятность произведения двух независимых собы­тий равно произведению их вероятностей, т. е. .

Следствие. Если события независимы в совокупности, то вероятность их произведения равна произведению их вероятностей.

.

Если вероятность события не является постоянной величиной, а изменяется в зависимости от некоторых предположений, для решения задач удобно использовать формулы полной вероятности и Байеса.

Допустим, производится эксперимент (опыт), об условиях которого можно сде­лать взаимно исключающих друг друга предположений (гипотез): . Другими словами, в результате эксперимента может реализоваться ровно одна из гипо­тез . Тогда вероятность события может быть найдена по формуле

. (2)

Формула (2) называется формулой полной вероятности. В частности, в случае двух гипотез формула полной вероятности будет иметь вид

(3)

Вероятности гипотез вычисляются до проведения эксперимента (опыта). Теперь предположим, что экспери­мент проведен, и при этом появилось событие . Спрашива­ется, как изменятся вероятности гипотез с учетом появления события ? Другими словами, нужно найти условные вероятности гипотез:. С этой целью используется следу­ющая формула Байеса (или Бейеса)

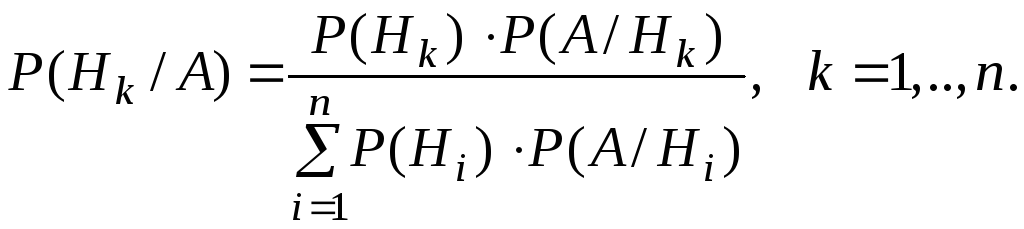(4)

Пусть проводится серия из независимых экспериментов (опытов, испытаний), в каждом из которых событие мо­жет либо появится, либо не появится. При этом эксперименты счита­ются независимыми, если вероятность появления события остается постоянной для всех экспериментов. Такая серия экспериментов называется схемой Бернулли. Пусть вероятность появления события в каждом из независимых экспериментов, . Нужно найти вероятность того, что при экспериментах событие появится ровно раз. Отметим, что эта вероятность обозначается и находится по следующей формуле Бернулли

(5)

причем 0!=1, .

Если в схеме Бернулли число экспериментов велико , то формула Бернулли (5) становится неудобной; в таком случае используются асимптотические (приближенные формулы Пуассона и Муавра –Лапласа.

Формула Пуассона используется в том случае, если вероятность появления события в каждом эксперименте мала . Форму­ла Пуассона имеет вид

, (6)

где параметр Пуассона. Отметим еще раз, что формула Пуассона (11.1) является приближенной; ее точность повышается с увеличением числа экспериментов .

Локальная формула Муавра-Лапласа используется в том случае, если вероятности и не очень малы . Эта формула име­ет вид

, (7)

где , .

В любом руководстве по теории вероятностей приводится таблица значений для функции Известно, что функция является четной, т. е. . Поэтому в таблице приводятся значения функции лишь для положительных значений аргумента.

Интегральная формула Муавра – Лапласа используется в схеме Бернулли для определения вероятности того, что при опытах собы­тие появится не менее раз и не более раз. Снова предполагается, что достаточно велико, а . Интегральная формула Муавра – Лапласа имеет вид

, (8)

где

, , .

Функция называется функцией Лапласа. В каждом руководстве по теории вероятностей приведена таблица значений функции .

Во-первых, функция нечетна, т.е. . Во-вторых, при . Поэтому в большинс­тве таблиц значения функции приведены только для значений аргумента .

Перейдем к рассмотрению случайной величины. Переменная величина называется случайной величиной, если ее значение можно определить только после эксперимента (опыта). Возможные значения случайной величины будем обозначать через . Вообще, условимся в дальнейшем случайные величины обозначать большими буквами латинского алфавита, а их воз­можные значения – соответствующими малыми буквами. Важным классом случайных величин являются дискретные случайные величины.

Случайная величина Х называется дискретной, если все ее значения можно перенумеровать. Для задания дискретной случайной вели­чины достаточно указать все ее возможные значения и вероятности, с которыми эти значения принимаются. Обычно такой закон записывают в виде таблицы, первая строка которая содержит значения случайной величины Х, а вторая – вероят­ности , с которыми эти значения принимаются. Такая таблица называется рядом распределения дискретной случайной величины.

Следует отметить, что в ряде распределения сумма вероятностей . (9)

Формула (1) обычно служит для контроля правильности сос­тавления закона распределения дискретной случайной величины. В частности, если соотношение (1) не выполняются, то ряд распре­деления для дискретной случайной величины составлен неверно.

Наиболее общей формой закона распределения, пригодной для любых случайных величин (как дискретных, так и непрерывных) является функция распределения.

Опр. 10. Функцией распределения случайной величины назы­вается вероятность попадания в интервал , т.е. вероятность того, что принимает значение, меньшее .

Это определение можно записать формулой: . Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является самой универсальной характеристикой случайной величины. В отличие от функции распределения более наг­лядное представление о характере распределения случайной величины дает ее плотность распределения (если она существует).

Опр. 11. Плотностью распределения случайной величины Х называется производная от функции распределения, т. е. .

Зная функцию распределения или плотность распределения случайной величины , несложно найти вероятность попадания в промежуток. Так если функция распределения случайной величины , то вероятность попадания в промежуток находится по формуле . (10)

Если же непрерывная случайная величина с плот­ностью распределения , то вероятность ее попадания в промежу­ток находится по формуле 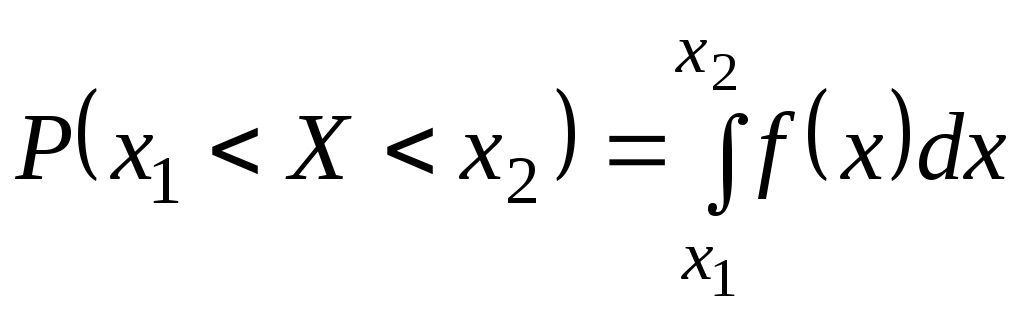. (11)

Функция распределения или плотность распределения полностью характеризуют случайную величину, но к сожалению, зачастую отыскание этих функций весьма затруднительно. Между тем для решения многих практических задач вовсе не нужно знать закон распределения слу­чайной величины. Достаточно знать лишь некоторые числа, характе­ризующие это распределение, так называемые, числовые характерис­тики случайной величины. Основными числовыми характеристиками случайной величины являются математическое ожидание и дисперсия.

Опр 12. Если Х - дискретная случайная величина с рядом расп­ределения

				. . .
				. . .

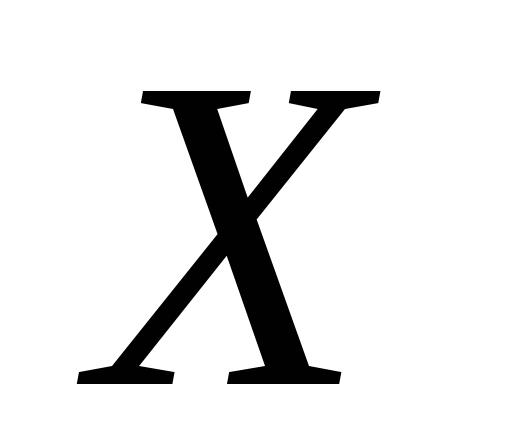
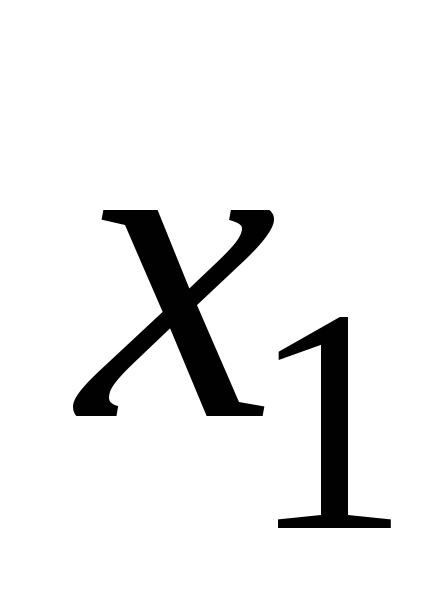
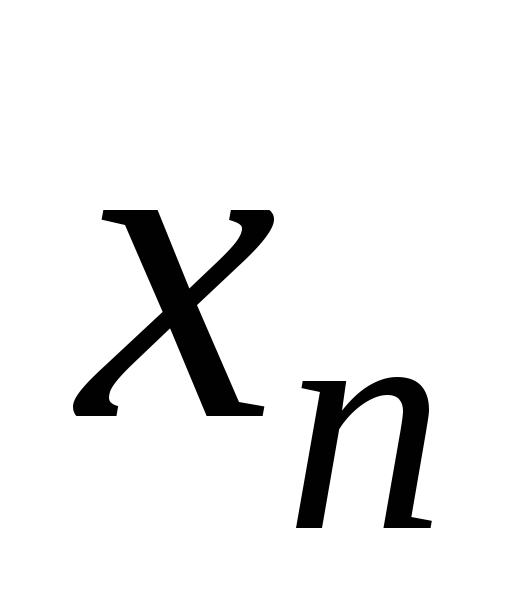
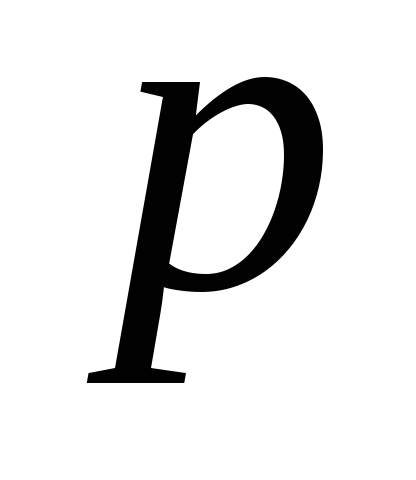
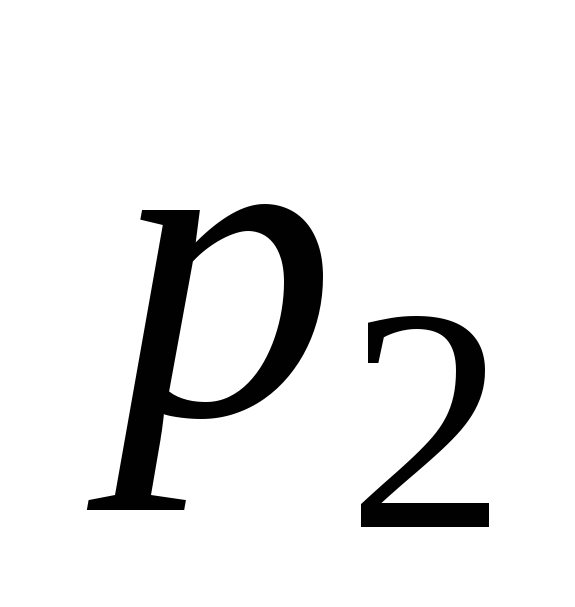
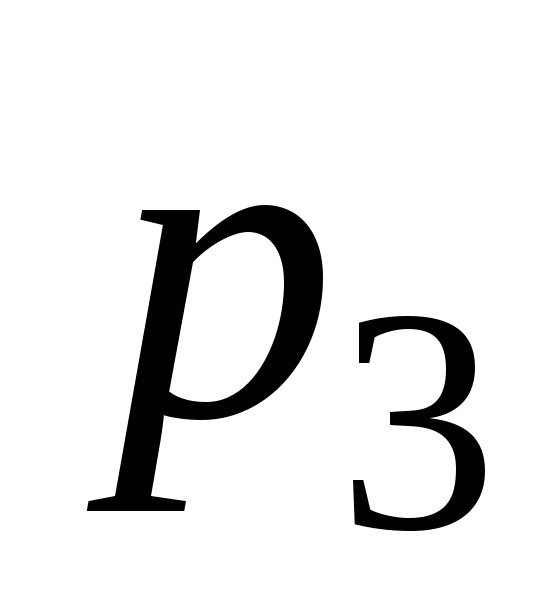
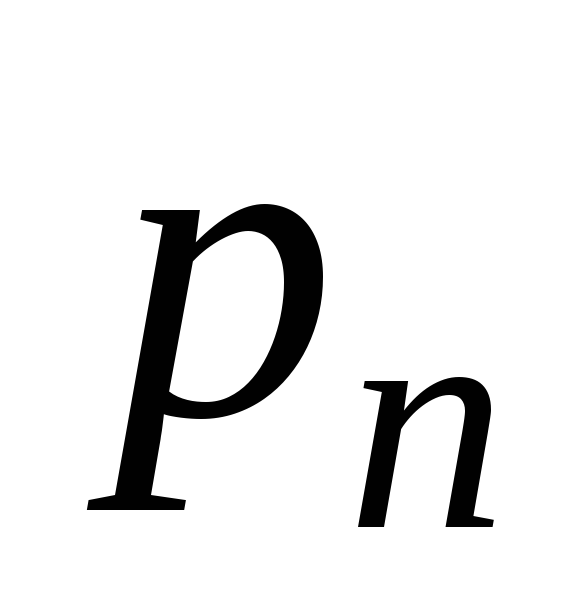
то ее математическим ожиданием М[X] (или ) называется сумма

произведений всех ее возможных значений на вероятности этих зна­чений, т. е.

(12)

Если Х - непрерывная случайная величина с плотностью распределения , то ее математическим ожиданием называется следующий интеграл

. (13)

Несмотря на различие определяющих формул (12) и (13), математическое ожидание M[X] всегда задает центр распреде­ления случайной величины Х, т.е. точку на оси абсцисс, около ко­торой группируются все возможные значения случайной величины Х. В этом состоит вероятностный смысл математического ожидания.

Опр 13. Дисперсией D[X] (или ) случайной величины Х называет­ся математическое ожидание квадрата ее отклонения от математичес­кого ожидания, т.е. .

Для дискретной случайной величины дисперсия находится по формуле

(14)

Для непрерывной случайной величины с плотностью распределения - по формуле

(15) Для нахождения дисперсии помимо (14), (15) обычно исполь­зуется формула

, (16)

утверждающая, что дисперсия случайной величины равна математичес­кому ожиданию ее квадрата минус квадрат ее математического ожида­ния. Именно формулу мы будем в дальнейшем использовать для отыскания дисперсии.

Хотя дисперсия является достаточно удобной характеристикой рассеивания случайной величины, она лишена наглядности, так как имеет размерность квадрата случайной величины. Поэтому зачастую вместо дисперсии используют квадратный корень из дисперсии; эта характеристика называется средним квадратическим отклонением и обозначается или. Итак, .

Опр. 14. Начальным моментом го порядка случайной величины Х называется математическое ожидание ой степени этой величины: .

Опр. 15. Центральным моментом го порядка случайной величины Х называется математическое ожидание ой степени ее отклонения от математического ожидания: .

Опр. 16. Коэффициентом асимметрии называется отношение третьего центрального момента к кубу среднего квадратического отклонения:

. (17)

Опр. 17. Коэффициентом эксцесса Eх[X] называется уменьшенное на 3 отношение четвертого центрального момента к четвертой степени среднего квадратического отклонения:

. (18)

Исключительно важную роль в теории вероятностей играет нормальный закон распределения.

Опр 18. Непрерывная случайная величина называется нормально распределенной (распределенной по закону Гаусса), если плотность ее распределения имеет вид

где параметры нормального распределения. Параметры имеют определенный вероятностный смысл: яв­ляется математическим ожиданием, средним квадратическим отк­лонением нормального закона распределения.

Функция распределения для нормального закона имеет вид

, где функция Лапласа.

Функция Лапласа играет важную роль в теории вероятнос­тей. Сформулируем ее основные свойства.

• Функция Лапласа монотонно возрастает на .

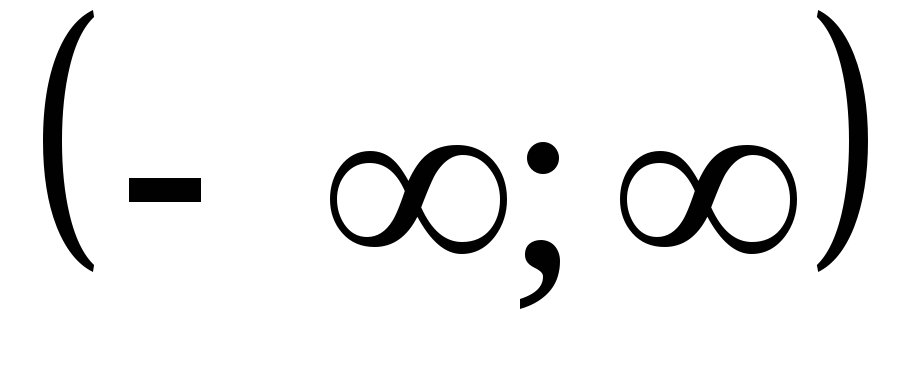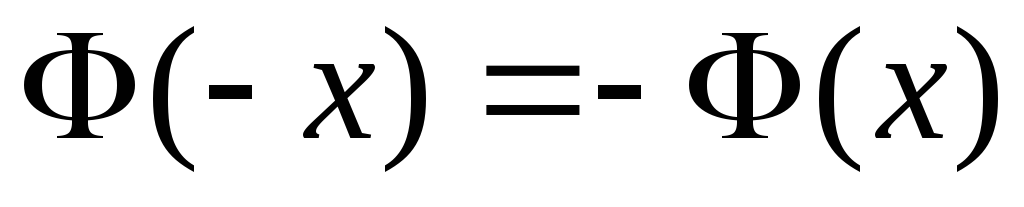• , т. е. функция Лапласа 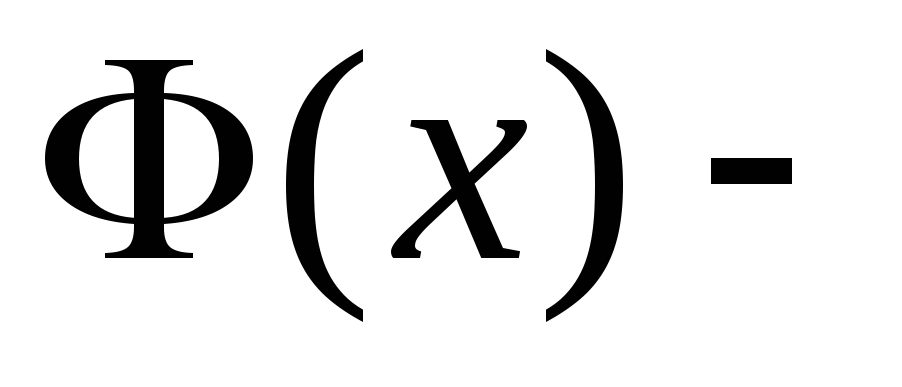нечетна.

• 

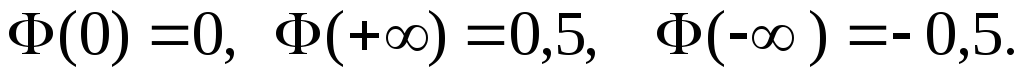
• Вероятность попадания нормально распределенной случайной величины в интервал (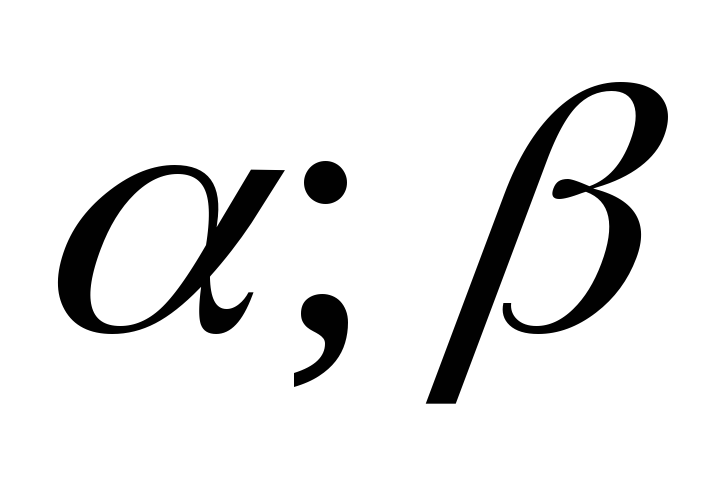) находится по формуле

Подчеркнем, что эта формула может используется только для нормально­го распределения; для других законов распределения следует ис­пользовать формулы (10) и (11).

Для нормального распределения справедливо правило трех сигм, состоящее в том, что, нормально рас­пределенная случайная величина с вероятностью, близкой к 1, принимает значения из интервала.

Опр 19. Непрерывная случайная величина Х называется равномерно распреде­ленной на отрезке [a;b], если ее плотность распределе­ния имеет вид

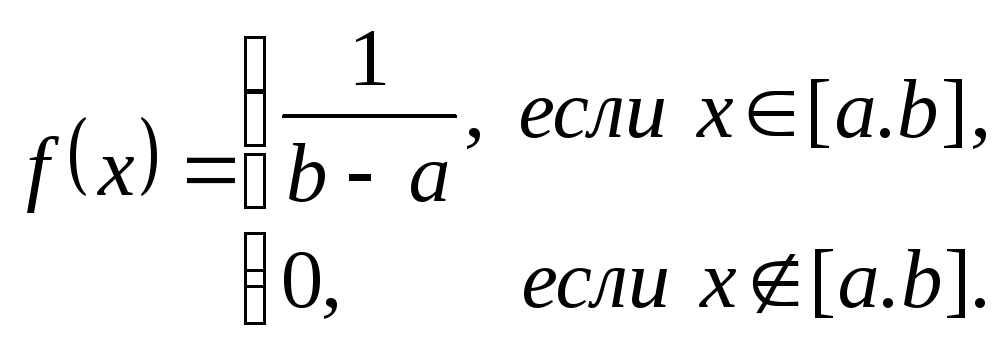
Известно, что математическое ожидание и дисперсия равномерно распределенной случайной величины находятся по формулам

Опр. 20. Говорят, что непрерывная случайная величина Х имеет показательный (экспоненциальный) закон распределения, если ее плотность распределения имеет вид

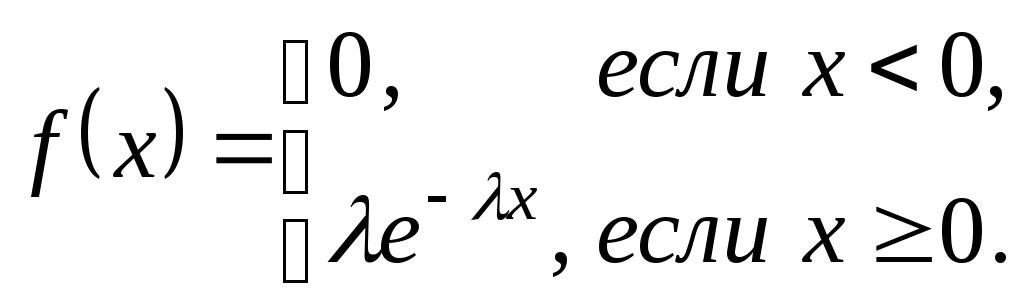
Величина >0 является параметром показательного распределения.

Доказывается, что для показательного распределения математическое ожидание и дисперсия равны