
-
Образец выполнения работы
Задача 1. Из урны, в которой лежат 10 красных, 12 синих и 8 зеленых шаров, наугад вытаскивается 6 шаров. Найти вероятность того, что будут вынуты 3 красных, 2 синих и 1 зеленый шар.
Решение.
Найдем общее число исходов. Вытащить
из урны 6 шаров означает составить группу
из 6 шаров, если всего 10+12+8=30 шаров; при
этом порядок извлечения шаров не
важен. Значит, речь идет о сочетаниях
по 6 элементам из 30. Число таких сочетаний
равно
![]() .
Следовательно,
.
Следовательно,
![]()
Найдем число
благоприятствующих исходов. Три красных
шара можно извлечь
![]() способами, два синих шара –
способами, два синих шара –
![]() способами, один зеленый шар –
способами, один зеленый шар –
![]() способами. Значит, по комбинаторному
правилу произведения
способами. Значит, по комбинаторному
правилу произведения
![]()
Находим
вероятность события
![]() Ответ: 0,333.
Ответ: 0,333.
Задача 2(а). Два стрелка произвели по выстрелу. Вероятность попадания в мишень первым стрелком равна 0,7 , вторым 0,6. Какова вероятность поражения мишени одной пулей?
Решение.
Введем события:
![]() – «мишень поражена одной пулей»,
– «мишень поражена одной пулей»,
![]() «первый стрелок попал в мишень»,
«первый стрелок попал в мишень»,
![]() «второй стрелок попал в мишень». По
условию
«второй стрелок попал в мишень». По
условию
![]() Тогда вероятности противоположных
событий равны
Тогда вероятности противоположных
событий равны
![]()
![]()
Так как
![]() и события
и события
![]() несовместны (т.е. не могут происходить
одновременно), то по следствию к теореме
1
несовместны (т.е. не могут происходить
одновременно), то по следствию к теореме
1
![]()
Но
события
![]() и
и
![]() независимы, значит,
независимы, значит,
![]() Следовательно,
Следовательно,
![]() Ответ: 0,46.
Ответ: 0,46.
Задача 2(б). Слово АБРАКАДАБРА разрезается на буквы, которые затем тщательно перемешиваются. Поочередно вытаскиваются 4 карточки и прикладываются одна к другой слева направо. Найти вероятность сложить слово КРАБ.
Решение. Введем вспомогательные события:
![]() -
«первой извлечена буква К»,
-
«первой извлечена буква К»,
![]() -
«второй извлечена буква Р»,
-
«второй извлечена буква Р»,
![]() -
«третьей извлечена буква А»,
-
«третьей извлечена буква А»,![]() -
«четвертой извлечена буква Б».
-
«четвертой извлечена буква Б».
Тогда
искомое событие
![]() .
По следствию к теореме 2
.
По следствию к теореме 2
![]()
Находим отдельно
каждую вероятность. Поскольку среди 11
карточек буква
![]() встречается 1 раз, то
встречается 1 раз, то
![]() .
Буква
.
Буква
![]() встречается 2 раза среди оставшихся 10
карточек, поэтому
встречается 2 раза среди оставшихся 10
карточек, поэтому
![]() .
В момент извлечения следующей буквы
осталось 9 карточек, на 5 из них написана
буква
.
В момент извлечения следующей буквы
осталось 9 карточек, на 5 из них написана
буква
![]() ;
поэтому
;
поэтому
![]() .
Наконец, в момент извлечения четвертой
буквы остается 8 карточек, на 2 из них
написана буква
.
Наконец, в момент извлечения четвертой
буквы остается 8 карточек, на 2 из них
написана буква
![]() ;
поэтому
;
поэтому![]() .
Теперь
.
Теперь
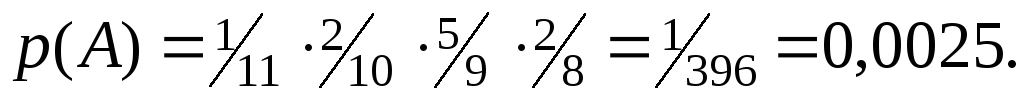 Ответ: 0,0025.
Ответ: 0,0025.
Задача 3. В магазин поступает продукция с трех предприятий – изготовителей. Их объемы поставок относятся как 6:3:1. Вероятности изготовления некачественной продукции для этих предприятий составляют соответственной 0,01, 0,02 и 0,03. Наугад купленное в магазине изделие оказалось некачественным. Какова вероятность того, что оно изготовлено на первом предприятии?
Решение.
Введем в рассмотрение событие
![]() «купленное изделие оказалось
некачественным». Введем систему гипотез:
«купленное изделие оказалось
некачественным». Введем систему гипотез:
-
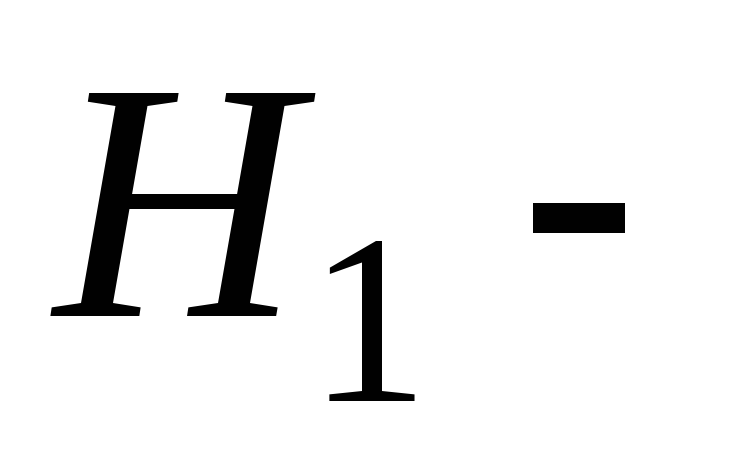 «изделие изготовлено
на 1-м предприятии»;
«изделие изготовлено
на 1-м предприятии»; -
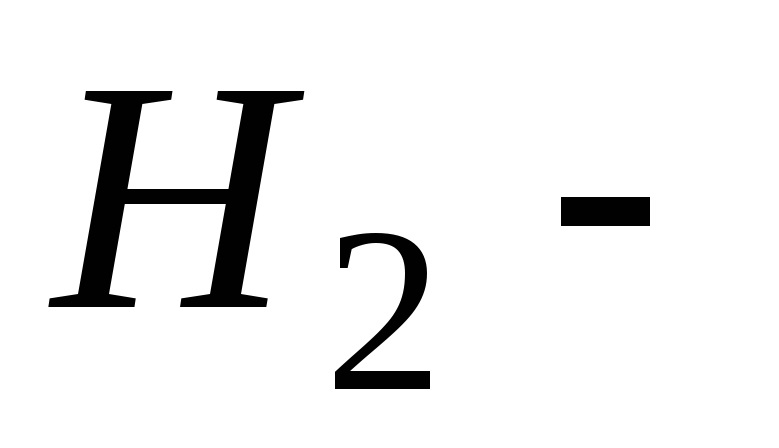 «изделие изготовлено
на 2-м предприятии»;
«изделие изготовлено
на 2-м предприятии»; -
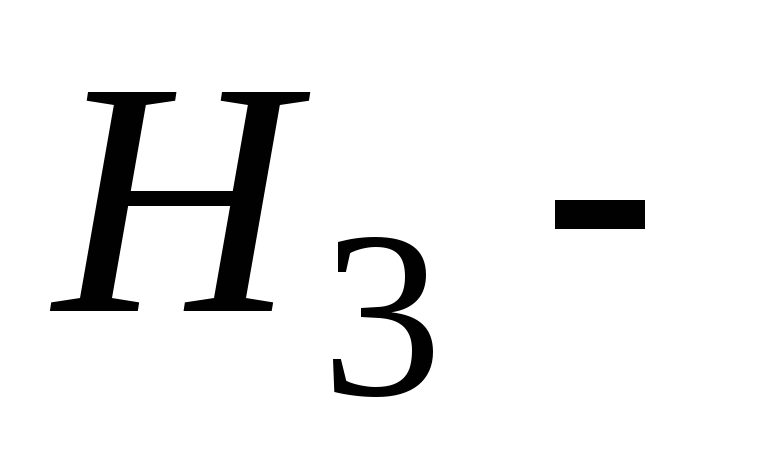 «изделие изготовлено
на 3-м предприятии».
«изделие изготовлено
на 3-м предприятии».
Находим
вероятности гипотез:
![]() ,
,
![]() ,
,
![]() .
Согласно условию задачи условные
вероятности события
.
Согласно условию задачи условные
вероятности события
![]() равны:
равны:
![]()
![]() ,
,
![]() .Теперь
найденные значения подставим в формулу
Байеса (4), получим
.Теперь
найденные значения подставим в формулу
Байеса (4), получим
![]()
![]() Ответ: 0,014.
Ответ: 0,014.
Задача 4(а). По мишени производится 5 выстрелов. Вероятность попадания при каждом выстреле равна 0,8. Определить вероятность двух попаданий в мишень.
Решение.
Используем формулу Бернулли (5) при
![]() .
Получаем
.
Получаем
![]() Ответ: 0,0512.
Ответ: 0,0512.
Задача 4(б). Вероятность обнаружения прибором элементарной частицы составляет 0,0005. Через прибор пропускается поток в 1000 частиц. Какова вероятность того, что прибор зарегистрирует не более двух частиц.
Решение.
Пусть
![]() число
элементарных частиц, зарегистрированных
прибором. Условие: «не более двух частиц»
означает, что или
число
элементарных частиц, зарегистрированных
прибором. Условие: «не более двух частиц»
означает, что или
![]() ,
или
,
или
![]() ,
или
,
или
![]() .
и события попарно несовместны, поэтому
искомая вероятность равна
.
и события попарно несовместны, поэтому
искомая вероятность равна
![]() .
.
Каждую из этих
вероятностей найдем по формуле Пуассона
(6). Согласно условию
![]() .
Находим
.
Находим
![]() .
Следовательно,
.
Следовательно,
![]()
![]() Значит,
Значит,
![]() .
.
Ответ 0,986
Задача 4(в). Вероятность поражения мишени при одном выстреле равна 0,8. Найти вероятность того, что при 100 выстрелах мишень будет поражена ровно 75 раз.
Решение.
Так как
![]() ,
то
,
то
![]() .
Число экспериментов
.
Число экспериментов
![]() =100
сравнительно велико,
=100
сравнительно велико,
![]() ,
поэтому для вычисления искомой
вероятности можно использовать локальную
формулу Муавра – Лапласа (7). Вычисляем
,
поэтому для вычисления искомой
вероятности можно использовать локальную
формулу Муавра – Лапласа (7). Вычисляем
![]() =
=
![]() .
.
Тогда
![]() .
Находим по таблице
.
Находим по таблице
![]()
![]() .
Значит,
.
Значит,
![]() .
Ответ: 0,0456.
.
Ответ: 0,0456.
Задача 4(г). Передается закодированное сообщение из 1100 символов. Вероятность ошибки при декодировании каждого символа составляет 0,01. Считая декодирование каждого символа независимым от других, найти вероятность того, что число ошибок в принятом сообщении не превышает 20.
Решение.
Применим интегральную формулу
Муавра-Лапласа (8), в которой положим
![]() =0,01;
=0,01;
![]() =1-0,01=0,99;
=1-0,01=0,99;
![]() =0;
=0;
![]() =20.
Вычисляем
=20.
Вычисляем
![]() ,
,
![]() . Получим
согласно (8)
. Получим
согласно (8)
![]() .
При этом мы учли нечетность функции
Лапласа. Далее по таблице находим
.
При этом мы учли нечетность функции
Лапласа. Далее по таблице находим
![]() (2,73)=0,4968
,
(2,73)=0,4968
,
![]() (3,33)=0,4995.
Значит,
(3,33)=0,4995.
Значит,
![]() = 0,4968+0,4995=0,9963. Ответ: 0,9963.
= 0,4968+0,4995=0,9963. Ответ: 0,9963.
Задача 5. Случайная величина Х, задана рядом распределения распределения
-
X
-2
1
3
4
6
7
p
0,21
0,31
0,20
0,15
0,05
0,08
Найти
![]() .
.
Решение.
Математическое ожидание
![]() находим по формуле (12).
находим по формуле (12).
![]()
Для
нахождения дисперсии воспользуемся
формулой (16). Для этого предварительно
найдем
![]() по формуле
по формуле
![]() .
Получим
.
Получим
![]()
Далее
по формуле (16) находим:
![]() Среднее квадратическое отклонение
найдем по формуле
Среднее квадратическое отклонение
найдем по формуле
![]()
Коэффициент асимметрии
![]() найдем по формуле (17). Для этого
предварительно найдем
найдем по формуле (17). Для этого
предварительно найдем
![]() по формуле
по формуле
![]()
Получим
![]()
![]()
Тогда по формуле (17)
![]()
Коэффициент эксцесса
![]() найдем по формуле (18). Для этого
предварительно найдем
найдем по формуле (18). Для этого
предварительно найдем
![]() по формуле
по формуле
![]()
Получим
![]()
Тогда по формуле (18)
![]()
Ответ:
![]()
Задача 6.
Непрерывная
случайная величина задана функцией
распределе-ния:
![]() при
при
![]()
![]() при
при
![]()
![]() при
при
![]() .
Найти вероятности того, что в результате
испытания
.
Найти вероятности того, что в результате
испытания
![]() примет значение из интервала
примет значение из интервала
![]() .
Найти
.
Найти
![]() .
.
Решение.
Сначала найдем плотность распределения
![]() ,
для этого продифференцируем функцию
распределения. Получим
,
для этого продифференцируем функцию
распределения. Получим
![]() при
при
![]() при
при
![]() .
.
Вероятность попадания в интервал находим по формуле (11). Получим
![]()
Математическое
ожидание
![]() найдем по формуле (13). Получим
найдем по формуле (13). Получим
![]()
![]()
Для
нахождения дисперсии воспользуемся
формулой (16). Для этого предварительно
найдем
![]() .
Получим
.
Получим
![]()
![]()
Далее
по формуле (16) находим:
![]() Среднее квадратическое отклонение
найдем по формуле
Среднее квадратическое отклонение
найдем по формуле
![]()
Ответ:
![]()
