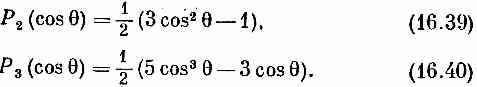§ 4. Матрица поворота для произвольного спина

Сейчас, я надеюсь, вам уже ясно, как важно представ­ление о моменте количества движения для понимания атомных процессов. До сих пор мы рассматривали только системы со спи­нами (или «полными моментами количества движения») 0, ¹/₂ и 1. Но бывают, конечно, и атомные системы с большими момента­ми количества движения. Для анализа таких систем нужны такие же таблицы амплитуд поворота, какие мы привели в гл. 15, § 6. Иными словами, нужна матрица амплитуд для спина ³/₂, 2, ⁵/₂, 3 и т. д. Мы не будем подробно рассчитывать эти таблицы, но хотели бы показать, как это делается, чтобы вы, если понадобится, могли сами это проделать.

Как мы видели раньше, любая система со спином, или «пол­ным моментом количества движения», j может существовать в одном из 2/ + 1 состояний, в которых z-компонента момента количества движения принимает одно из дискретных значе­ний j, j-1, j -2, . . ., -(j-1), -j (все в единицах h). Обозначая z-компоненту момента количества движения про­извольного выбранного состояния через mh, можно определить состояние момента количества движения, задав численные значения двух «квантовых чисел момента количества движения» j и m. Такое состояние можно отметить, указав вектор состоя­ния | j, m>. В случае частиц со спином ¹/₂ могут быть два состоя­ния | ¹/₂, ¹/₂) и | ¹/₂, -¹/₂> a состояния системы со спином 1 в этих обозначениях можно записать как |1, +1>, |1, 0>, | 1, -1>. У частицы со спином 0 может быть, конечно, лишь одно

состояние | 0, 0>.

Теперь мы можем посмотреть, что происходит, когда мы прое­цируем общее состояние | j, m> на представление, относящееся к повернутой системе осей. Прежде всего известно, что j — это число, которое характеризует систему, поэтому оно не меняется. При повороте осей мы получим просто смесь различных значе­ний т для одного и того же j. В общем случае появится амплиту­да того, что система в повернутой системе координат окажется в состоянии | j, m'>, где m' — новая z-компонента момента ко­личества движения. Значит, нам нужны матричные элементы <j, m' |R|j, m> всевозможных поворотов. Мы уже знаем, что бывает, если поворот делается на угол  вокруг оси z. Новое состояние — это попросту старое, умноженное на e^im, у него по-прежнему то же значение т. Это можно записать так:

или, если вам больше нравится,

(где _m,m' равно единице при m' = m, и нулю в прочих случаях).

При поворотах вокруг любой другой оси возникает переме­шивание различных m-состояний. Можно было бы, конечно, попытаться подсчитать матричные элементы для произвольных поворотов, описываемых углами Эйлера , и . Но будет легче, если мы вспомним, что самый общий такой поворот может быть составлен из трех поворотов R_z(), R_y(), R_z(); так что если мы знаем матричные элементы для поворотов вокруг оси y, то уже располагаем всем необходимым.

Как же нам найти матрицу поворота для поворота частицы со спином j на угол  вокруг оси у? Опираясь на основные за­коны (и на то, что уже было), это сделать нелегко. Мы так посту­пали со спином ¹/₂: вывели все, что нужно, пользуясь довольно сложными соображениями симметрии. Для спина 1 мы это про­делали уже иначе: рассмотрели частный случай, когда система со спином 1 складывается из двух систем со спином ¹/₂. Если вы последуете за нами и признаете правильным тот факт, что в общем случае ответы зависят только от спина j, а не от того, как скреплены между собой разные части системы со спином j, то мы сможем обобщить рассуждения для спина 1 на произвольный спин. Мы сможем, например, соорудить искусственную систему со спином ³/₂ из трех объектов со спином ¹/₂. Мы сможем даже избежать всяких усложнений, вообразив, что все они суть различные частицы — скажем, протон, электрон и мюон. Преобразуя каждый объект со спином ¹/₂, мы увидим, что происходит со всей системой — надо только вспомнить, что для комбинированного состояния все амплитуды перемножаются. Давайте посмотрим, как все это проходит.

Допустим, мы расположили все три объекта со спином ¹/₂ спинами вверх; обозначим такое состояние |+++>. Если мы взглянем на него из системы координат, повернутой относительно оси z на угол , то каждый плюс останется плюсом, но умно­жится на е^i/2. Таких множителей у нас тройка, так что

Ясно, что состояние |+++> — это как раз то, что мы назы­ваем состоянием m=+³/₂, или состоянием |³/₂, + ³/₂>.

Если мы затем повернем эту систему вокруг оси у, то у каж­дого из объектов со спином ¹/₂ появится некоторая амплиту­да стать плюсом или стать минусом, так что вся система станет теперь смесью восьми возможных комбинаций |+++>,

|++->, |+-+>, |-++>, |+-->, |-+->,

|--+> или |--->. Ясно, однако, что их можно раз­бить на четыре группы, чтобы каждая соответствовала своему значению m. Прежде всего мы имеем |+++>, для которого m=³/₂. Затем имеется тройка состояний |++->, |+-+> и |-++> — каждое с двумя плюсами и одним минусом. Поскольку каждый из объектов со спином ¹/₂ имеет равные шансы стать после поворота минусом, то каждая из этих трех комбинаций должна войти на равных паях. Поэто­му возьмем комбинацию

где множитель 1/3 поставлен для нормировки. Если мы по­вернем это состояние вокруг оси z, то получим множитель e^i/2 для каждого плюса и e^-i/2 для каждого минуса. Каждое слагаемое в (16.27) умножится на e^i/2, и общий множитель е^i/2 мы вынесем за скобки. Такое состояние соответствует нашему представлению о состоянии с m=+¹/₂; мы приходим к выводу, что

Точно так же можно написать

что соответствует состоянию с m=-¹/₂. Заметьте, что мы берем только симметричные сочетания, у нас нет комбинаций, куда входят слагаемые со знаком минус. Они отвечали бы со­стояниям с таким же т, но с иным j. Это аналогично случаю спина 1, где (1/2){|+->+|-+>} было состоянием | 1,0>, а (1/2){|+->-|-+>} было состоянием | 0,0>. Наконец, мы имеем

Эта четверка состояний сведена в табл. 16.1.

Таблица 16.1 • СВОДКА СОСТОЯНИЙ

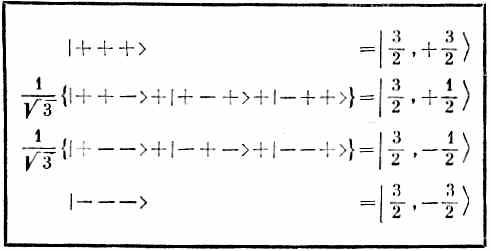
Все, что нам теперь нужно сделать, это взять каждое состоя­ние, повернуть его вокруг оси у и посмотреть, сколько новых состояний оно создаст — пользуясь известной нам матрицей поворота для частицы спина ¹/₂. Можно поступать так же, как мы это делали в случае спина 1 [см. гл. 10, § 6 (вып. 8)]. (Только алгебры будет побольше.) Мы будем строго следовать идеям гл. 10 (вып. 8), так что подробных объяснений давать не будем. Состояния в системе S будут обозначаться

и т. д.; T-системой будет считаться система, повернутая вокруг оси у системы S на угол . Состояния в T-системе будут обозна­чаться |³/₂, + ³/₂, Т>, |³/₂, + ¹/₂, Т> и т. д. Ясно, что | ³/₂, + ³/₂, Т> это то же самое, что | +' + ' + ' > (штрихи всегда относятся к T-системе). Точно так же |³/₂, +¹/₂, Т> будет равняться

и т. д. Каждое |+'>-состояние в T-системе получается как из |+>-, так и из |->-состояний в системе S с помощью матрич­ных элементов из табл. 10.4 (вып. 8, стр. 267).

Если мы имеем тройку частиц со спином ¹/₂, то (10.47) надо заменить на

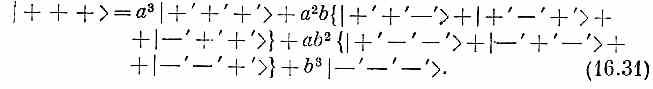
Пользуясь обозначениями табл. 10.4, получим вместо (10.48) уравнение

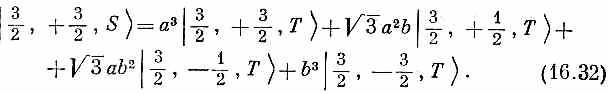
Это уже дает нам некоторые из наших матричных элементов <jT| iS>. Чтобы получить выражение для ³/₂, +¹/₂, S> мы дол­жны исходить из преобразования состояния с двумя плюсами и одним минусом. К примеру,

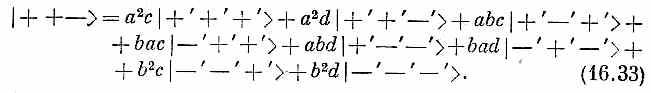
Добавляя два сходных выражения для + — +> и | — + +> и деля на ]/3, найдем

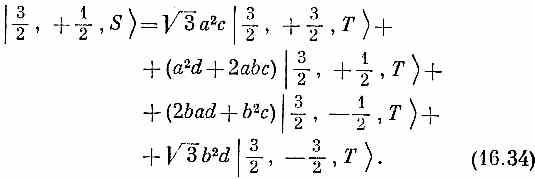
Продолжая этот процесс, мы найдем все элементы <jТ|iS> матрицы преобразования. Они приведены в табл. 16.2. Первый столбец получается из (16.32), второй — из (16.34). Последние два столбца были вычислены таким же способом. Теперь допустим, что T-система была повернута относительно S-системы на угол  вокруг ее оси у. Тогда а, b, с и d равны [см. (10.54), вып. 8]: а=d=cos/2, с=-b=sin/2. Под­ставляя это в табл. 16.2, получаем формулы, похожие на вторую половину табл. 15.2, но на этот раз для системы со спином ³/₂.

Таблица 16.2 • МАТРИЦА ПОВОРОТА ДЛЯ ЧАСТИЦЫ СО СПИНОМ ³/₂

Коэффициенты а, b, с и d объясняются в табл. 10.4.

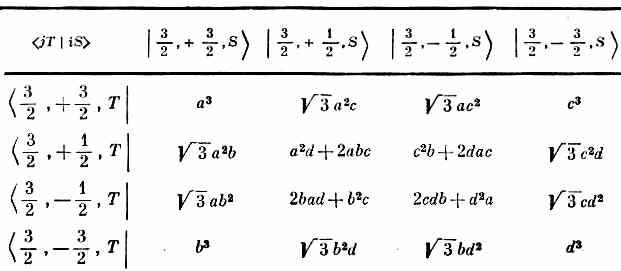
Рассуждения, которые мы только что провели, были обобще­ны на систему с произвольным спином j. Состояния |j, m> можно составить из 2j частиц со спином ¹/₂ у каждой. (Из них j+m будут в ] + >-состоянии, а j-m будут в |->-состоянии.) Проводится суммирование по всем возможным способам, какими их можно сочетать, а затем состояния нормируются умноже­нием на надлежащую постоянную. Если у вас есть способности к математике, то вы сможете доказать, что получается следую­щий результат:

где k пробегает все те значения, при которых под знаком факториала получаются неотрицательные величины.

Это очень запутанная формула, но с ее помощью вы сможете проверить табл. 15.2 для j=1 (стр. 129) и составить ваши собственные таблицы для больших j. Некоторые матричные элементы очень важны и получили особые наименования. Например, матричные элементы для m= m'=0 и целых j известны под названием полиномов Лежандра и обозначаются </, 0 |

Первые из них таковы:

P₀(cos)=l, (16.37)

p₁(cos)=cos, (16.38)