§ 5. Выпрямление на полупроводниковом переходе

Теперь мы покажем, как получается, что p—n-переход дей­ствует как выпрямитель. Если мы к переходу приложим напря­жение одного знака, то пойдет большой ток, если другого — тока почти не будет. А если к переходу приложить переменное напряжение, то ток пойдет только в одну сторону — он «выпря­мится». Посмотрим еще раз, что получается в условиях равно­весия, описанных кривыми фиг. 12.9. В материале p-типа имеет­ся высокая концентрация N_p положительных носителей. Эти носители повсюду диффундируют, и некоторое их количество каждую секунду приближается к переходу. Этот ток положи­тельных носителей, достигающих перехода, пропорционален N_p. Большая часть их, однако, разворачивается обратно, не будучи в состоянии взять высокий потенциальный холм у пере­хода, и только доля их проходит дальше. Имеется также ток положительных носителей, приближающихся к пе­реходу с другой стороны. Этот ток тоже пропорционален плот­ности положительных носителей в n-области, но здесь плотность носителей намного ниже плотности в p-области. Когда положи­тельные носители приближаются из n-области к переходу, они обнаруживают перед собой холм с отрицательным склоном и сходу соскальзывают под гору, на p-сторону перехода. Обо­значим этот ток I₀. В условиях равновесия токи в обе стороны одинаковы. Значит, можно ожидать, что будет выполняться следующее соотношение:

Вы замечаете, что оно на самом деле совпадает с (12.10). Мы просто вывели его другим способом.

Допустим, однако, что мы снизили напряжение на n-стороне перехода на величину V — это можно сделать, приложив к переходу внешнюю разность потенциалов. Теперь разница в потенциалах по обе стороны потенциального холма уже не V, а V-V. У тока положительных носителей из p-области в n-область теперь в показателе экспоненты будет стоять именно эта разность потенциалов. Обозначая этот ток через I_1; имеем

Этот ток превосходит ток I₀ в раз. Значит, между I₁ и I₀ существует следующая связь:

Ток из p-области при приложении внешнего напряжения V растет по экспоненте. А ток положительных носителей из n-области остается постоянным, пока V не слишком велико.

Достигая барьера, эти носители по-прежнему будут видеть перед собой идущий под гору потенциал и будут все скатываться в p-область. (Если V больше естественной разности потенциа­лов V, положение может измениться, но что случается при таких высоких напряжениях, мы рассматривать не будем.) В итоге ток положительных носителей I, текущий через переход, будет определяться разницей токов в обе стороны:

Дырочный ток I течет в n-область. Там дырки диффундируют в самую глубь n-области и могут, вообще говоря, аннигилиро­вать на основной массе отрицательных носителей электронов. Убыль электронов, теряемых при этой аннигиляции, воспол­няется током электронов из внешнего контакта материала n-типа.

Когда V=0, то и ток в (12.14) равен нулю. Если V положительна, ток с напряжением резко растет, а если V отрицательна, знак тока меняется, но экспоненциальный член вскоре становится пренебрежимо малым, и отрицательный ток никогда не превышает I₀ — величины, которая, по нашему предположению, очень мала. Этот обратный ток I₀ ограничен той слабой плотностью, которой обладают неосновные носители в n-области перехода.

Если вы проведете в точности тот же анализ для тока отри­цательных носителей, текущего через переход, сперва без внешней разности потенциалов, а после с небольшой приложен­ной извне разностью потенциалов V, то для суммарного электронного тока вы опять получите уравнение, похожее на (12.14). Поскольку полный ток есть сумма токов носите­лей обоего рода, то (12.14) применимо и к полному току, если только отождествить I₀ с максимальным током, кото­рый может течь при переме­не знака напряжения.

Вольтамперная характеристика (12.14) показана на фиг. 12.10.

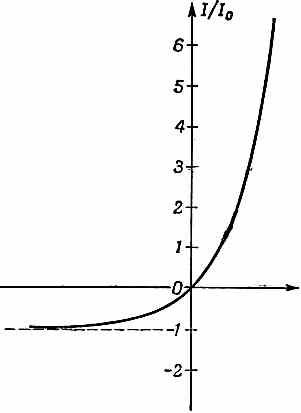
Фиг. 12.10. Зависимость тока через переход от приложенного к нему напряжения.

Она демонстрирует нам типичное поведение кристаллических диодов, подобных тем, которые применяются в современных вычислительных машинах. Нужно только заметить, что (12.14) справедливо лишь при невысоких напряжениях. При напряже­ниях, сравнимых с естественной внутренней разностью потен­циалов V (или превышающих ее), в игру входят новые явления и ток уже не подчиняется столь простому уравнению.

Быть может, вы вспомните, что в точности такое же уравне­ние мы получили, говоря о «механическом выпрямителе» — храповике и собачке [см. гл. 46 (вып. 4)]. Мы получали те же уравнения, потому что лежащие в их основе физические про­цессы весьма схожи.