2. Неравенства Маркова и Чебышева

Неравенство Маркова в литературе иногда называется леммой Маркова или леммой Чебышева, так как оно является частным случаем неравенства Чебышева.

Неравенство Маркова ². Если значения случайной величины Х неотрицательны и существует ее математическое ожидание М(Х) = а, то для любого положительного числа ε справедливо неравенство:

P(Х ≥ ε) ≤ . (2.1)

События Х < ε и Х ≥ ε – противоположные, поэтому, используя неравенство (2.1), получаем

Р(Х < ε)=1 – Р(Х ≥ ε) ≥ 1 – . (2.2)

Выражения (2.1–2.2) справедливы для дискретных и непрерывных случайных величин.

Доказательство. Нам потребуется следующее понятие. Пусть А – некоторое событие. Назовем индикатором события А случайную величину I(A), равную единице, если событие А произошло, и нулю, если А не произошло. По определению, величина I(A) имеет распределение Бернулли с параметром р = Р(I(A) = 1) = Р(A), и ее математическое ожидание равно вероятности успеха р = Р(A), т. е. М(I(A)) = 1∙р + 0∙q = р = Р(A).

Индикаторы прямого и противоположного событий связаны равенством I(A) + = 1. Поэтому

X = X ∙ I(Х < ε) + X ∙ I(Х ≥ ε) ≥ X ∙ I(Х ≥ ε) ≥ ε ∙ I(Х ≥ ε).

Тогда

М(Х) ≥ М(ε ∙ I(Х ≥ ε)) = ε ∙ М(I(Х ≥ ε)) = ε ∙ P(Х ≥ ε). (2.3)

Осталось разделить обе части неравенства (2.3) на положительное число ε:

P(Х ≥ ε) ≤ .

Что и требовалось доказать.

Пример 2.1. Дано распределение вероятностей случайной величины X:

Xi	2	4	6	8	10	12
Pi	0,1	0,2	0,25	0,15	0,15	0,15

Пользуясь неравенством Маркова, оценить вероятность того, что случайная величина X примет значение, меньшее 11.

Решение. Используя неравенство Маркова (2.2), получаем

М(Х) = 2·0,1 + 4·0,2 + 6·0,25 + 8·0,15 + 10·0,15 + 12·0,15 = 7;

Р(Х < 11) ≥ 1 – = 1 – ≈ 1 – 0,636 = 0,364.

Таким образом, Р(Х < 11) ≥ 0,364.

Ответ: Р(Х < 11) ≥ 0,364.

Пример 2.2. Сумма всех вкладов в некоторой сберегательной кассе составляет 20 млн. руб., а вероятность того, то случайно взятый вклад меньше 100000, равна 0,8. Каково число вкладчиков сберегательной кассы?

Решение. Пусть X – величина случайно взятого вклада, а n – число всех вкладчиков. Тогда из условия задачи следует, что

М(Х) = ; Р(X < 100000) = 0,8.

Используя неравенство Маркова, получаем

Р(X < 100000) ≥ 1 – .

Следовательно,

0,8 ≥ 1 – ;

≥ 0,2;

200 ≥ n·0,2;

n ≤ 1000.

Ответ: число вкладчиков сберегательной кассы составляет не более 1000.

Если известна дисперсия случайной величины, то с ее помощью можно оценить вероятность отклонения этой величины на заданное значение от своего математического ожидания, не зная распределения случайной величины. Эта задача была решена русским математиком П. Л. Чебышевым³ в 1867 г. Он доказал неравенство для неотрицательной случайной величины X, имеющей M(X) и D(X).

Неравенство Чебышева. Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине будет меньше данного положительного числа ε, ограничена снизу величиной , т. е.

Р(|X – M(X)| < ε) ≥ 1 – . (2.4)

Из неравенства (2.4) переходом к противоположному событию можно получить:

Р(|X – M(X)| ≥ ε) ≤ . (2.5)

Доказательство. Если ε > 0, то неравенство |X – M(X)| ≥ ε равносильно неравенству (X – M(X))² ≥ ε², поэтому

Р(|X – M(X)| ≥ ε) = Р((X – M(X))² ≥ ε²).

Применим неравенства Маркова (2.1):

Р(|X – M(X)| ≥ ε) = Р((X – M(X))² ≥ ε²) ≤ = .

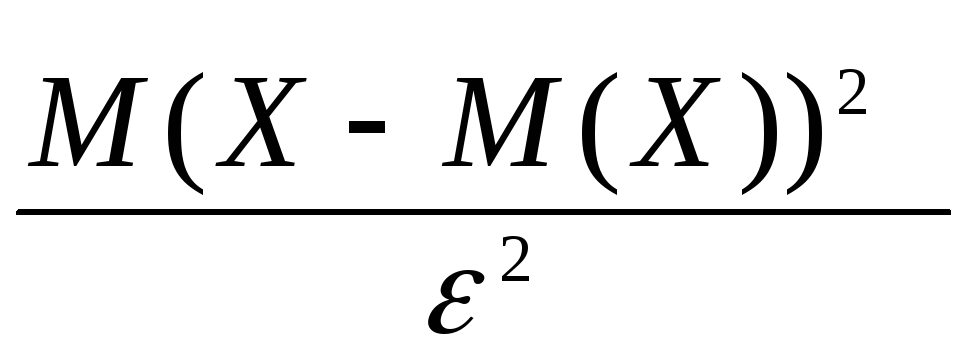Таким образом,

Р(|X – M(X)| ≥ ε) ≤ .

Что и требовалось доказать.

Неравенство Чебышева дает лишь грубые оценки сверху для вероятностей событий вида (|X – M(X)| < ε). Это “плата” за то, что нам не известен закон распределения вероятностей.

В качестве следствия получим так называемое «правило трех сигм», которое означает, что вероятность случайной величины отличаться от своего математического ожидания более чем на утроенное среднее квадратическое отклонение мала. Так, если оценивать вероятность этого события для нормально распределенной случайной величины X, не зная, что она нормально распределена, то

P(|X– а| ≥ 3σ) ≤ = ≈ 0,111...

Ранее (см. тема «Случайные величины»: «правило трех сигм») было найдено точное значение, равное 0,0027. Отсюда видно, что точное значение вероятности в 40 (!) раз меньше ее грубой оценки, полученной на основании неравенства Чебышева. Разумеется, для каждого распределения величина этой вероятности своя.

Пример 2.3. Вероятность наступления некоторого события р = 0,3 в каждом из n = 900 независимых испытаний. Используя неравенство Чебышева, оценить вероятность того, что событие повторится от m₁ = 240 до m₂ = 300 раз.

Решение. По условиям задачи имеет место биномиальный эксперимент. Следовательно, математическое ожидание и дисперсия для биномиального распределения будут равны:

М(X) = пр = 900∙0,3 = 270; D(X) = npq = 900∙0,3∙0,7 = 189;

ε = |240–270| = |300–270| = 30.

Значит,

Р(|X–270| ≤ 30) ≥ 1 – = 1 – = 1 – 0,21 = 0,79.

Ответ: Р(|X–270| ≤ 30) ≥ 0,79.

Пример 2.4. Среднесуточное потребление электроэнергии в населенном пункте равно 20000 кВт∙ч, а среднее квадратическое отклонение – 200 кВт∙ч. Какое потребление электроэнергии можно ожидать в этом населенном пункте в ближайшие сутки с вероятностью, не меньшей 0,96?

Решение. По условию задачи M(X) = 20000 кВт∙ч, σ(X) = 200 кВт∙ч и

Р(|X – M(X)| < ε) ≥ 0, 96.

Из неравенства Чебышева (2.4) следует, что 1 – = 0,96. Определим ε:

= 0,04;

ε² = , или ε = = = = 1000 кВт∙ч.

Таким образом, используя неравенство М(Х) – ε < X < М(Х) + ε, получим

20000 1000 < X < 20000 + 1000.

Ответ: Ожидается потребление электроэнергии в пределах от 19000 до 21000 кВт∙ч.